Title: Asteroids for microhertz gravitational-wave detection
Authors: Michael A. Fedderke, Peter W. Graham, Surjeet Rajendran
First Author’s Institution: Department of Physics and Astronomy, The Johns Hopkins University, Baltimore, MD, USA
Status: Preprint on arXiv
Imagine what astronomy would be like if we only had optical telescopes – no spaceborne X-ray observatories like Chandra, massive interferometers like the Very Large Array, or next-generation infrared telescopes like JWST. We’d miss out on so much of the universe, from massive clouds of hydrogen to supermassive black holes to the earliest galaxies. The same is true of gravitational wave astronomy. Our main window into the gravitational wave universe comes courtesy of interferometers like LIGO, Virgo and KAGRA in the 10 hertz to 10 kilohertz range, watching for merging pairs of compact objects, like neutron stars and stellar-mass black holes. These instruments are complemented by emerging methods like pulsar timing arrays (1 to 100 nanohertz) and future projects like LISA and other space-based interferometers (0.1 to 100 millihertz). However, this flock of detectors still only provides partial frequency coverage of the gravitational wave sky. There are several frequency ranges left untouched, including a notable gap around 1 microhertz. Today’s paper sketches out a novel method to patch up that hole in the microhertz range: asteroids with lasers!
Let’s take a step back. Gravitational waves are ripples in spacetime, stretching and compressing space as they move through the cosmos. The fractional change in length they induce is referred to as the strain, which oscillates in time and decreases farther from the source of the waves. To detect a passing gravitational wave, astronomers need to observe its effects on some object, often referred to as a test mass. In the case of Michelson interferometers like LIGO, these test masses are four mirrors made of fused silica, two along each massive arm. A laser beam bounces between each pair of mirrors; as gravitational waves pass by, they stretch spacetime, and change the length of the path the light travels by only 1/10,000th the width of a proton. When the beams from each mirror pair are combined, they produce an interference pattern, which scientists search for tell-tale signs of gravitational waves.
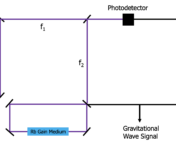
The instrument proposed in today’s paper is somewhat similar, but on much grander scales. The authors propose using a pair of asteroids as test masses, as shown in Figure 1. Each asteroid would be equipped with a transmitter and receiver accompanied by an atomic clock, either in orbit or on the asteroid itself. Pulses would be sent between the asteroids, and by measuring how long it takes each pulse to make a round trip, the atomic clocks would determine the distance between the asteroids. Gravitational waves would cause tiny changes to this distance and therefore to the time interval measured by the clocks. The contraption would be most sensitive to gravitational waves with frequencies near ~10 microhertz, in between LISA and pulsar timing arrays, thanks to the headache of the observational astronomer: noise.
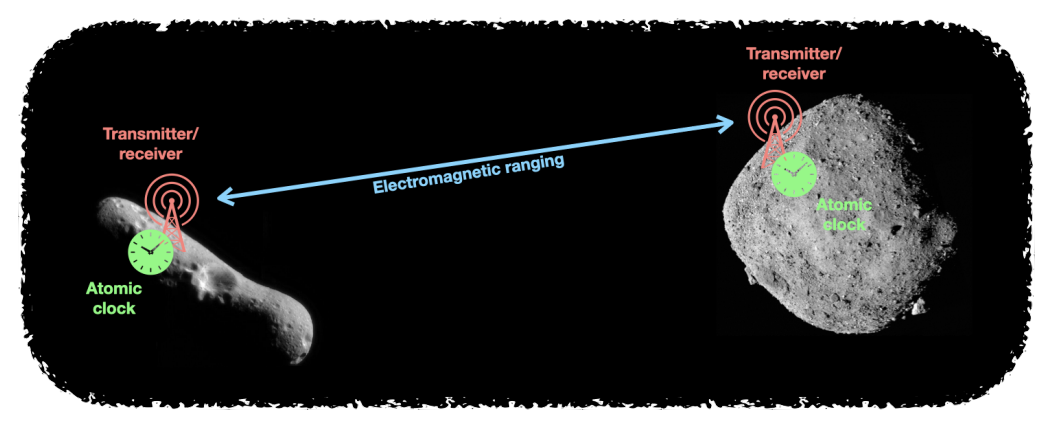
Figure 1: A sketch of the proposed detector, showing the transmitting/receiving stations and accompanying atomic clocks. Figure 1 in the paper.
Like any instrument, gravitational wave detectors suffer from different types of noise – unwanted emission that gets in the way of the signal being searched for. Michelson interferometers are forced to contend with everything from thermal fluctuations to seismic shifts to photon shot noise – not to mention the occasional thirsty raven. These combine to form a frequency-dependent sensitivity curve; sources with strains above the curve can be detected, while sources below the curve cannot. The sensitivity curve for LIGO is shown in Figure 2:
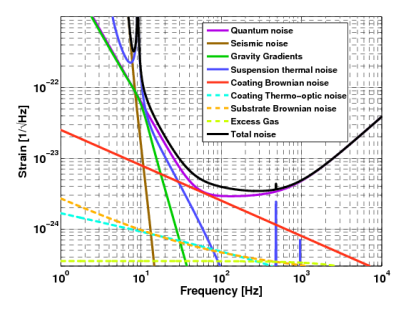
Figure 2: The sensitivity curve for the LIGO detectors. The curve results from a balance between several different sources of noise. At low frequencies, seismic noise from the Earth’s crust becomes important; at high frequencies, quantum effects and shot noise become important. This means that maximum sensitivity is reached at frequencies near 500 hertz. Image credit: Andreas Freise, Daniel Brown, Beijing Summer School.
The authors of today’s paper needed to calculate a sensitivity curve for their device to figure out what it could detect. They identified numerous sources of noise, which can be grouped into two categories. The first is called test-mass noise and causes unwanted, difficult-to-model changes to the motion of the asteroids. It includes:
- Changes in forces acting on the asteroid’s center of mass, including fluctuations of the Sun’s radiative output and the solar wind, as well as collisions with meteoroids and electromagnetic effects from plasma in the interplanetary medium
- Torques affecting the asteroid’s rotation, arising from the above sources as well as flybys from other asteroids
- Contributions from the movement of the asteroid as a rigid body, such as orbital and rotational motion
- Internal excitations, such as tidal forces, seismic noise and thermal expansion
The second category is called metrology noise and arises from the limited precision of the equipment used. It includes:
- Link noise from the limitations of the transmitters and receivers “linking” the two asteroids
- Clock noise from limitations on how precisely the light travel time can be measured
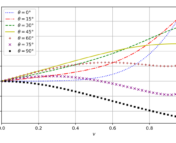
When combined, the various sources of noise yield the sensitivity curve shown in Figure 3. At low frequencies, noise from the Sun dominates; at high frequencies, metrology noise dominates.
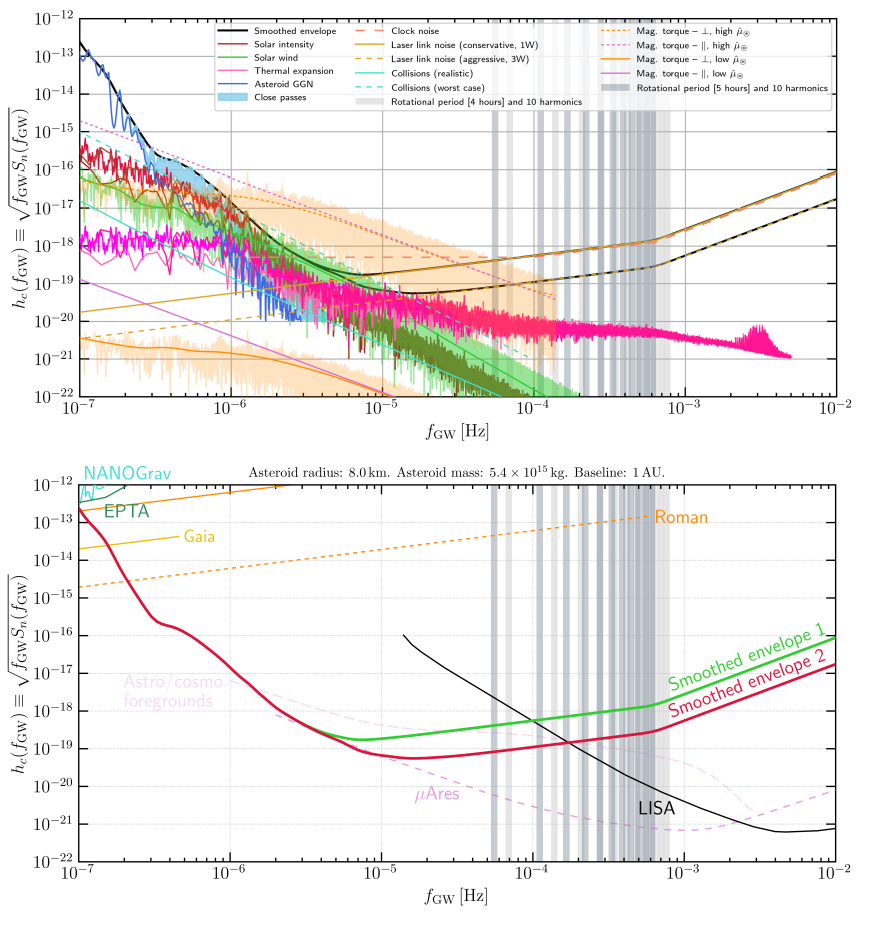
Figure 3: The sensitivity curve for the asteroid-based detector proposed in the paper. The top panel shows the miscellaneous sources of test mass and metrology noise, as well as the sensitivity curve created by adding them together. The bottom panel shows a smoothed version of the curve, along with sensitivity curves from other gravitational wave detectors, including LISA, µAres and pulsar timing arrays. The two different portions of the curve at higher frequencies were derived from alternate sets of assumptions about the setup. Created from Figure 8 and Figure 9 of the paper.
What could this asteroid-based gravitational wave detector see? We can get an idea from the white paper that proposed the µAres interferometer, another instrument geared toward the microhertz range. Our paper’s detector could set its sights on high-redshift intermediate-mass black holes or certain merging supermassive black holes. There might be a few double white dwarf binaries visible, as well as binary stellar-mass black holes within the Milky Way – all of which lie at frequencies inaccessible to the gravitational wave detectors of today. While there’s no guarantee that lasers on asteroids will be able to detect them – or that this instrument will ever be built – it’s an exciting possibility. In the rapidly-growing field of gravitational wave astronomy, even the most unusual ideas might be worth a try.
Astrobite edited by: Abygail Waggoner
Featured image credit: Figure 1 in the paper.