This guest post was written by Sayyed Ali Rafi, an astronomy student from Indonesia currently pursuing a Master’s degree at the University of Tokyo, Japan. Their current research involves characterizing ultra Hot Jupiter’s atmosphere through day-side spectrum in NIR domain using high-resolution data from Subaru/IRD. Outside of their research, they are a cat-person and love to do some hardcore-gaming activities.
Title: Six transiting planets and a chain of Laplace resonance in TOI-178
Authors: A. Leleu, Y. Alibert, N. C. Hara, M. J. Hooton, T. G. Wilson, P. Robutel, et al.
First Author’s Institution: Observatoire Astronomique de l’Université de Genéve, Chemin Pegasi 51, Versoix, Switzerland
Status: Published in A&A [open access], available on arXiv
While more than 3500 stars that are known to harbor planet(s), only about 800 of them harbor more than one planet. TOI-178 is an even rarer example, with six planets orbiting it! There are only 8 other stars that have the same number of planets! Moreover, this system is known to have the so-called Laplace resonance (a special type of resonance which we will dive into later), which is found only in 6 other multi-planetary systems. Resonance in such systems is a very interesting phenomenon because it gives us valuable information about how planetary systems form and evolve. This makes TOI-178 a very special case to study. So let’s dig into the system.
Getting the parameters
First, how did the authors find the planets? To first learn about the presence of the planets, they use TESS transit data. Later, they conducted follow-up transit observations with three optical-to-near IR telescopes: a space-based telescope, CHEOPS, and two ground-based ones, NGTS and SPECULOOS. The initial observations, when combined with their follow-up, revealed the existence of six planets with periods of 1.91, 3.24, 6.55, 9.96, 15.24, and 20.71 days (planet b, c, d, e, f, and g respectively). The authors use Bayesian inference to find the best fit model for the transit data assuming circular orbits (Figure 1). When the best fit is found, the planetary parameters could be extracted. In modelling transits, you can infer several parameters such as the planet’s radius and inclination, but not the planet’s mass.
To get even more details on these planets (such as inferring its mass), the authors conducted radial velocity observations with ESPRESSO. The authors used this data to obtain the mass (and hence the density) of the planets by again assuming circular orbits.
A dance of harmony
After all parameters were obtained, the authors found that this system has mean-motion resonances (MMRs). MMR are orbital configurations where a pair of planets has a period ratio equal or close to a simple integer ratio. In other words, if a pair of planets has a period ratio of 2:1 for instance, then the outer planet completes one of its periods exactly when the inner planet completes two. Our system has the following period ratio: Pc/Pb≈5/3, Pd/Pc≈2/1, Pe/Pd≈3/2, Pf/Pe≈3/2, and Pg/Pf≈2/1. When a pair doesn’t have an exact MMR (which is the case for all of those pairs), it is convenient to define the “distance” to the exact resonance expressed as the so-called “resonant angles”, . The authors then found that the time derivative of for c-d, d-e, e-f, and f-g pair has roughly the same value (~1.37°/day). So what does this mean? It indicates that the difference between the angles for the different pairs is practically zero! But what is the importance of this? Well, the authors explained that this condition leads to the presence of Laplace resonance: a three-body resonance where each consecutive pair has a close to or exact MMRs. The Laplace resonance chain in this system in period ratio is 2:4:6:9:12 from planet c to g (with three Laplace resonances from c-d-e, d-e-f, and e-f-g pair), or 18:9:6:4:3 in orbit ratio. In other words, As one example, planet c completes 18 orbits when planet d completes 9, and so on. This Youtube video from ESO shows animation of the resonances in this system.
Beautiful, isn’t it? What a dance of harmony.
What does resonance mean for the system?
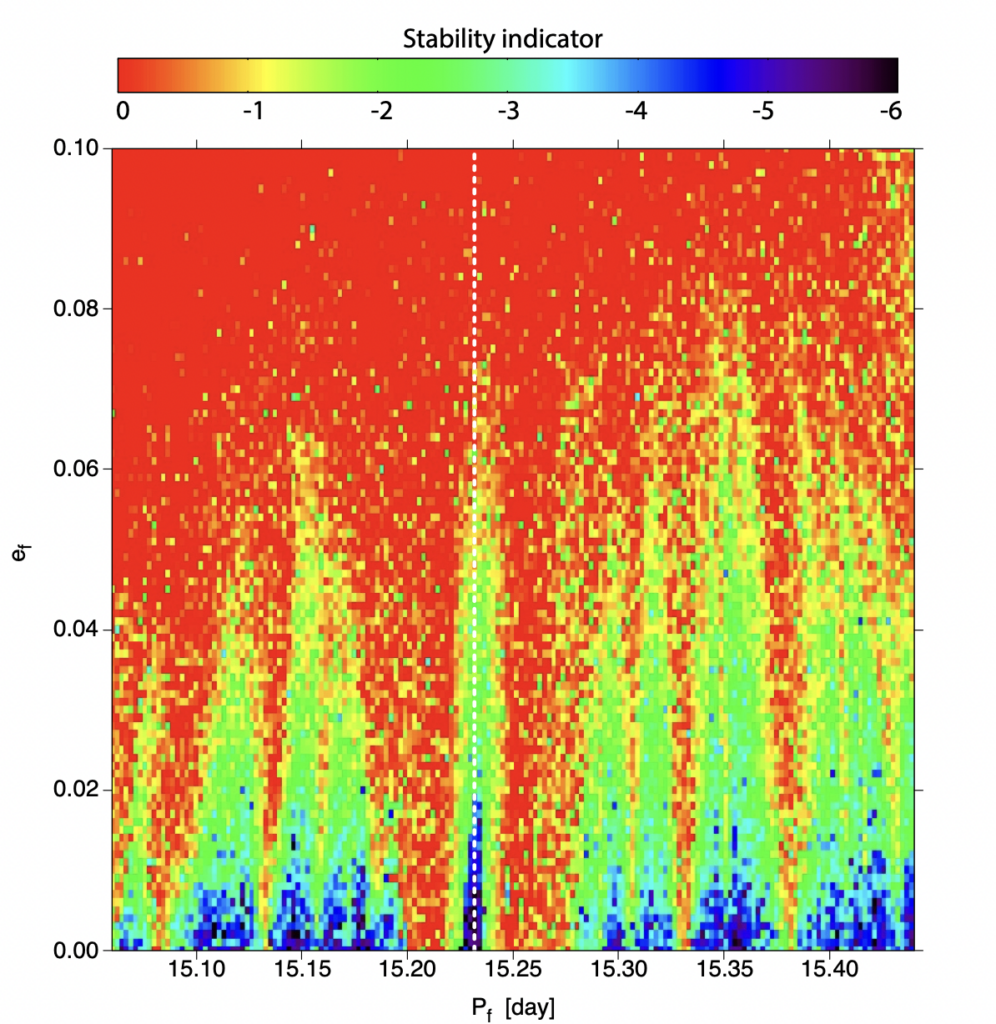
Well, the resonances seem to greatly stabilise it. Take planet f for instance. Figure 2 shows that in order for planet f to remain stable, the eccentricity must be very small, given a stable period. The same map is also produced for the other planets and shows the same features. These results indicate that the stability of the system is highly dependent on eccentricity, and that zero eccentricity gives the most stable solution for a given period. The green spikes in the map are the possible MMRs. They show a relatively stable region for e<0.01.
The other stability maps the authors present in the paper lead to the same conclusions: the orbital and physical parameters (and hence the resonances) that the authors obtained from the light curve fit lead to a very stable solution for this system, at least for the next several hundred thousand years.
A hope
Lastly, what about the habitability of TOI-178? TOI-178’s habitable zone is located at a distance of 0.2 AU or at a period of roughly 40 days. Sadly, none of the six planets orbiting it seem to lie in this zone. But, the truth is, there is no theoretical reason that limits the number of planets in this system. In fact, the authors explained that the MMR chain doesn’t have any reasons to stop at planet g – there could be additional, undetected planets in this system. One of the limitations to detect additional planets is that the available dataset is limited. Thus, conducting some additional observations with a longer time baseline could possibly reveal a planet inside, or at least very close to, the habitable zone, which is very exciting!
Wrapping it all up
Thanks to the Laplace resonances the planets are bound to, TOI-178 hosts a planetary system that will be stable at least for several hundred thousand years. Although none of its planets lie in the star’s habitable zone, theoretical predictions indicate that an additional and undetected planet exists and lies very close to the zone. This planetary system will likely be the main target for future orbital studies!
Image Credit: ESO/L. Calçada
Astrobite Edited by: Alice Curtin