Title: Finding mountains with molehills: the detectability of exotopography
Authors: Moiya A.S. McTier, David M. Kipping
First Author’s Institution: Department of Astronomy, Columbia University, New York, NY, USA
Status: Published in MNRAS [open access]
The rocky planets in our solar system have a large range of topographical features, such as mountain ranges, craters, and deep trenches and canyons. Today’s authors, Moiya McTier and David Kipping, are testing the boundaries of exoplanet detection to see if it’s possible to pick out the topography of planets around other stars. Observing these features outside of our solar system would be a huge step forward in expanding our characterization of exoplanets, and could be a useful way to identify planets undergoing processes like internal heating and plate tectonics.
Modeling blobby planets
Usually when we think about transiting exoplanets, we imagine the planet as a simple circle, like in Figure 1. In this picture, the cross section of the planet always looks the same, even if the planet is rotating. This means the transit signal will be a smooth line, since the planet will be blocking a constant amount of light.
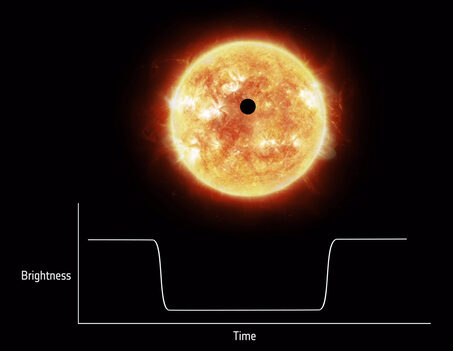
Figure 1: Diagram of a transit for a perfectly circular planet. In this case, the amount of light blocked by the planet remains at a constant minimum during the transit, but if the planet had surface features we should see some variation in that middle part of the graph. Image Credit: ESA
Planets with large-scale topography, like Olympus Mons on Mars, will have slightly different silhouettes when seen from different angles. Since the amount of light blocked by a transiting planet depends on the area of its silhouette compared to the area of the star, the transit signal should vary depending on which features are visible. For example, if a mountain comes into view on the transiting planet’s surface, the amount of light blocked by the planet should increase for a little while.
Quantifying bumpiness
The authors use the topographies of the rocky solar system bodies (Mercury, Venus, Earth, Mars, and the Moon) to understand how different surface features would manifest in transit data. They define the bumpiness of each object as the range of radial distances to each point on the planet’s surface, so a really mountainous planet would get a higher bumpiness score than a smoother planet.
The authors then calculate how the cross sectional area of a planet changes as the planet rotates, and use the changes in area to find the resulting variations in transit depth. Figure 2 shows how this is applied to a rotating earth. The blue outline shows the Earth with its oceans while the brown is what the Earth would look like as a dry planet. The ocean helps to smooth out the surface of Earth, so the ocean Earth has a lower bumpiness score than the dry Earth. Since the dry Earth is bumpier, it shows more variation in the relative brightness while the ocean-bearing Earth results in a fairly constant relative brightness.
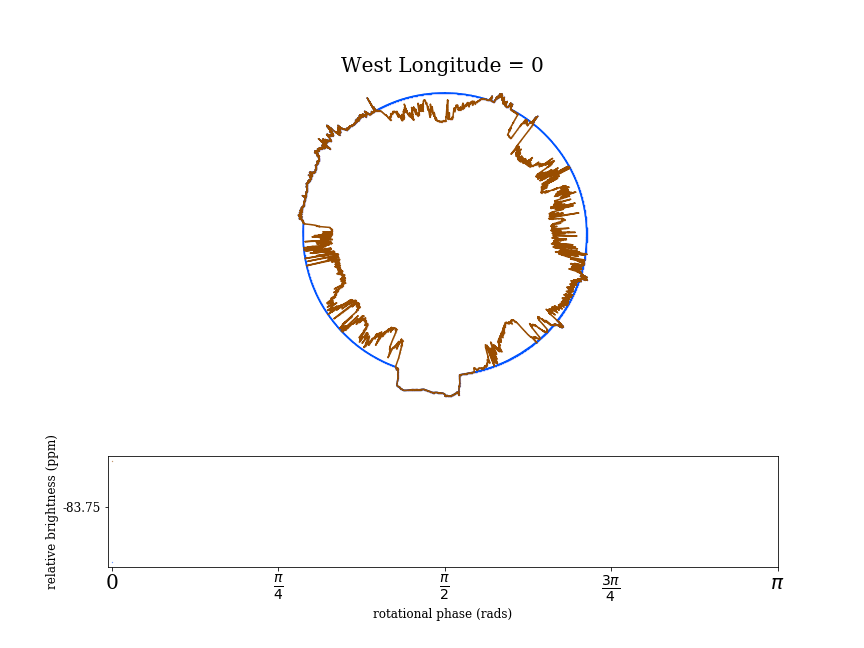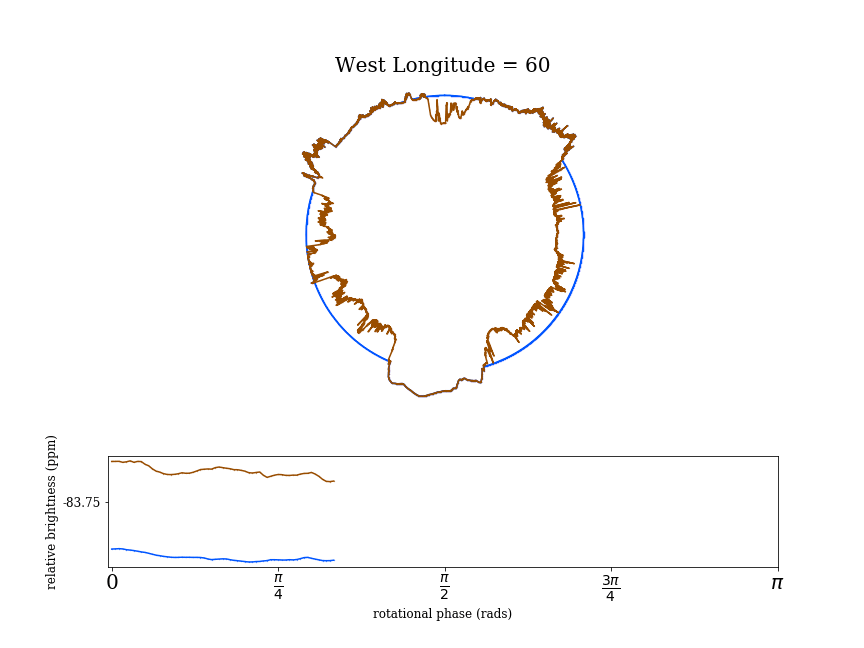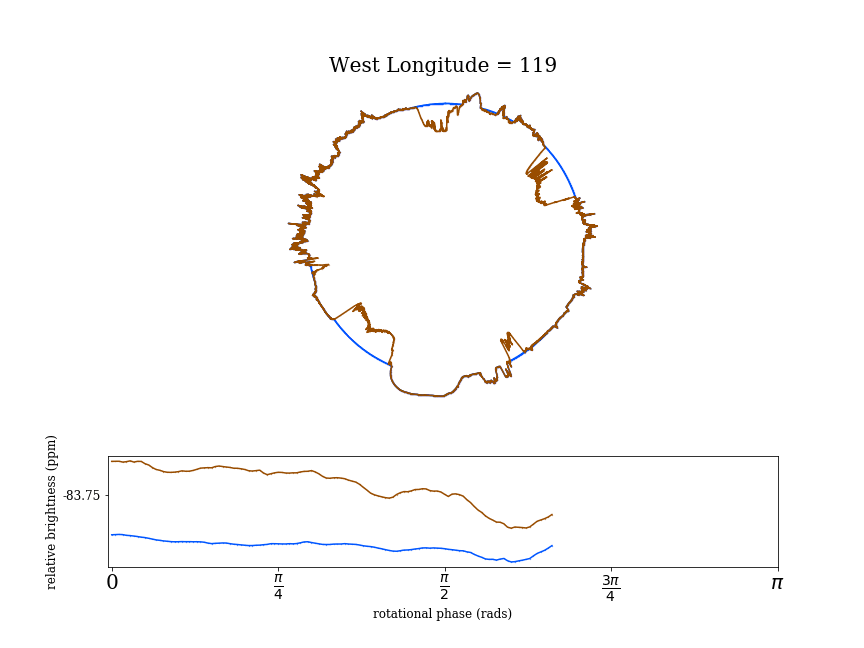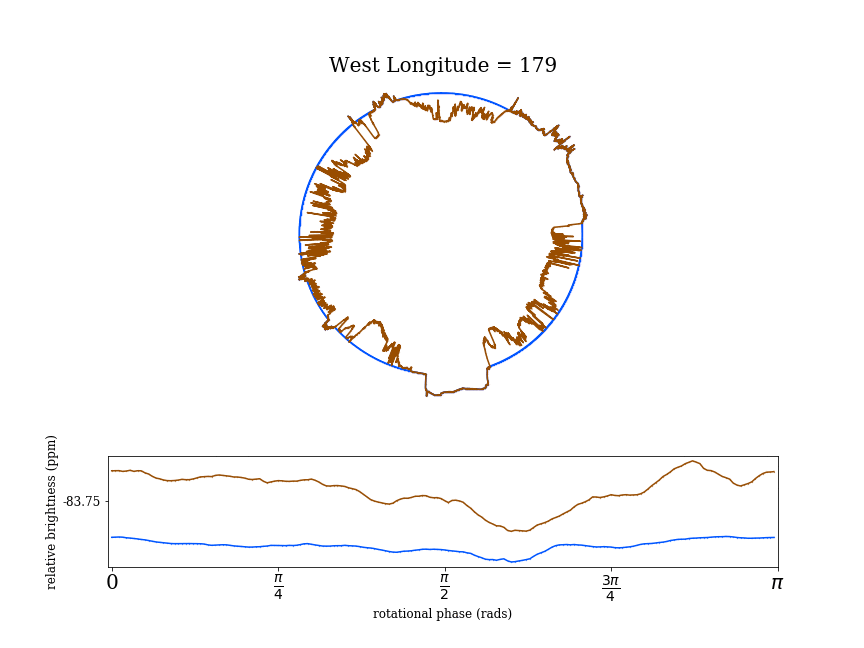
The authors carry out this calculation for each of the rocky solar system objects, and plot the bumpiness score against the amount of variation in the resulting transit (Figure 3). Out of the solar system objects, Mars is the bumpiest object, closely followed by dry Earth, and both have the largest variations in blocked light due to their surface features.
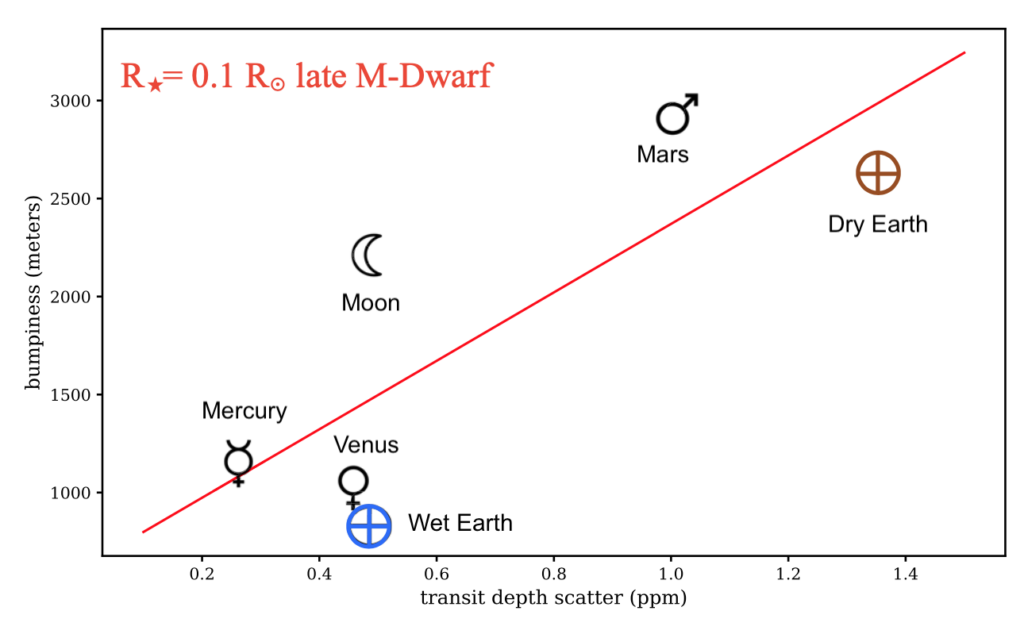
Figure 3: The bumpiness factor and resulting variation in transit depth calculated for the rocky solar system bodies, if they were passing in front of a low-mass star. Roughly, bumpier objects will have more variation in their transits. Image Credit: Adapted from Figure 6 from today’s paper
Exoplanets with texture
So could we see some exo-mountains in the near future? Unfortunately, we probably can’t make any topology measurements with currently operating telescopes. To resolve the difference between signals with and without surface features a really high precision is needed, and that’s not quite reached by today’s instruments. However, the next generation of “super” telescopes like the Extremely Large Telescope or Colossus could be up for the job! The authors calculate that these telescopes could identify planets with overall Mars-like bumpiness orbiting low mass stars, like white dwarfs. So it might just be a matter of time before we start mapping exo-topographies!
Astrobite edited by: Sasha Warren
Featured Image Credit: MPS/René Heller, WDW Magazine





Would be possible (& if of any use) to unwrap Figure 2 and place it on (say) a Mercator Projection of Earth?