Title: Consequences of dynamically unstable moons in extrasolar systems
Author: Bradley M. S. Hansen
First Author’s Institution: Mani L. Bhaumik Institute for Theoretical Physics, UCLA, CA, USA
Status: accepted to MNRAS [closed access]
The study of ‘exomoons’ — moons around extrasolar planets — has flourished in recent years. Though the existence of such systems has long been a theoretical expectation (and is a reasonable extrapolation of the abundance of moons in our own solar system), observing exomoons is understandably difficult, given the stark difference in size and mass between these moons and their host planets. Indeed, it was only in 2018 that the first exomoon candidate was observed. Since that point, observations of transiting planets have yielded more candidates, but the available samples have been limited to giant, Jupiter-like planets (for which transits are relatively easier to observe).
The formation of the closest-orbiting, rocky planets remains an open question in planetary science — some believe that such planets could form in-situ, meaning that they coalesce and grow close to the star, while others argue that these planets form in the outer disk and then migrate inward to their current positions. Giant impacts that can produce moons are a natural consequence in the former of these scenarios and are comparatively rarer in the latter, so observations of moons around rocky planets could be a smoking gun for the in-situ formation channel. However, observing moons around smaller, rocky planets (such as our own) is a challenging endeavor and direct observations will likely remain difficult for some time.
That said, indirect signatures of these moons might be observable today and such observations could shed light on the formation mechanisms of these compact planets, as is discussed in today’s paper. With this in mind, today’s paper focuses on the late time evolution of exomoon orbits around their host planets, accounting for different processes that result in various eventual outcomes for these satellites.
[Tides] spin me right round
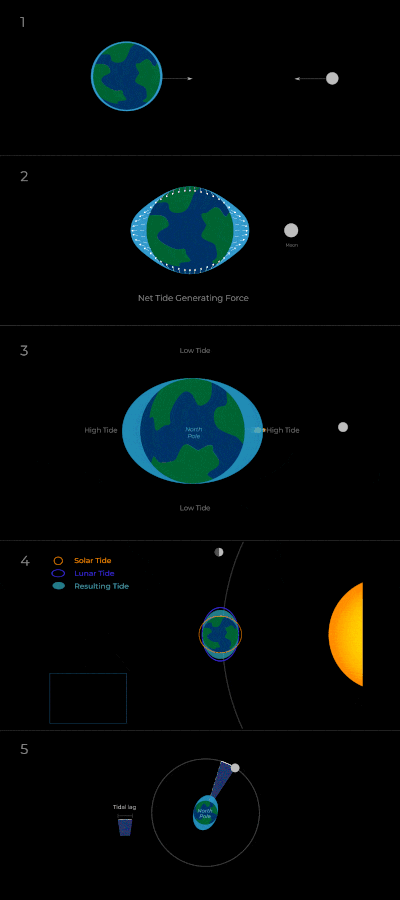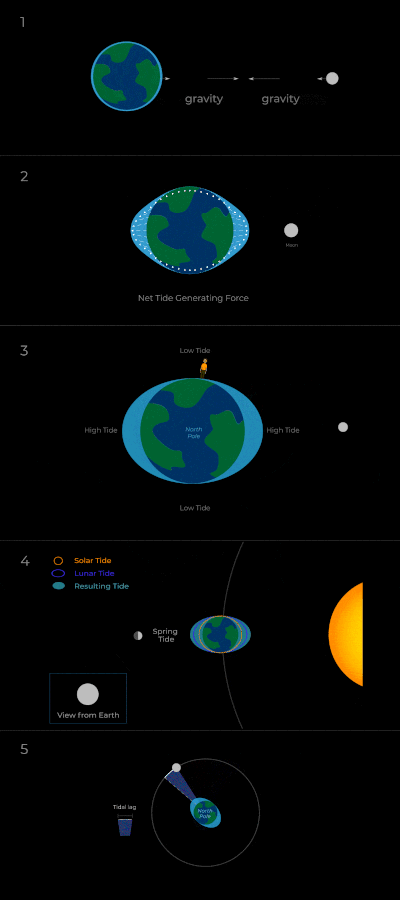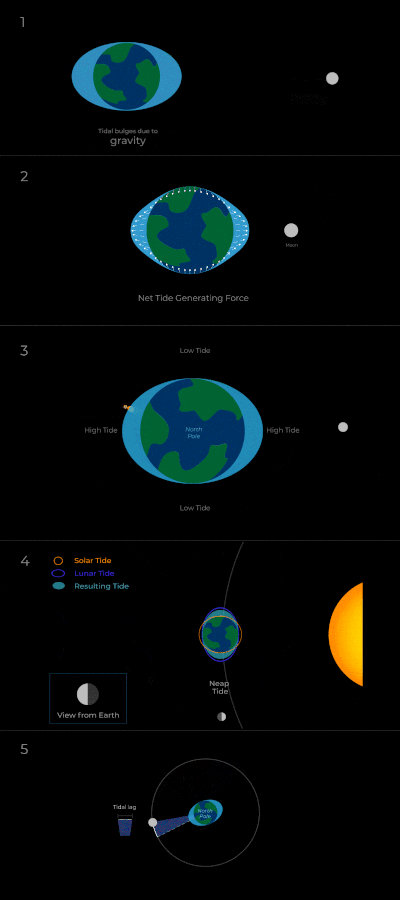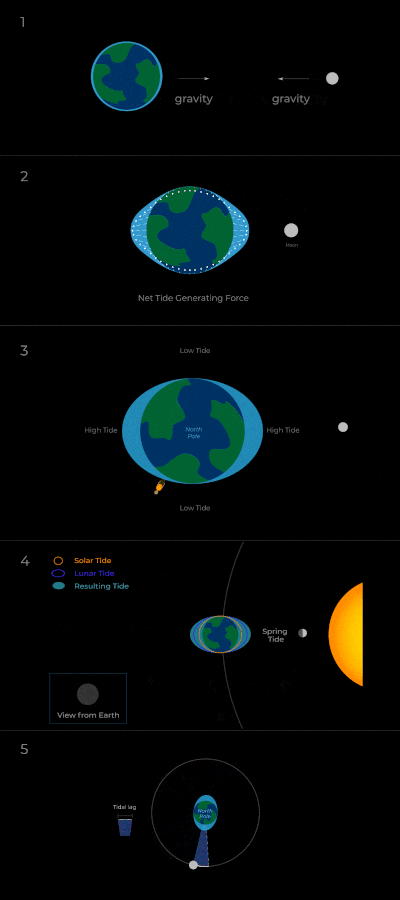
To study potential observational signatures, today’s author first studies the long-term behavior of moons in various configurations around their host planets. Conventional tidal theory dictates that the relative magnitude of a moon’s orbital speed around its planet and the planet’s spin determines how the moon’s orbit changes—i.e., whether it grows or shrinks. Tidal forces result from differences in the gravitational field experienced by objects across their extent (e.g., the side of the Earth closest to the Moon feels a stronger attraction to the Moon than the other side). Intuitively, we can think of this as producing a bulge in the planet along the line connecting the center of mass of the planet and the moon (see panels 1 and 2 in Figure 1).
However, real planets are more complicated than this—because of the planet’s spin and frictional forces within the body of the planet, the tidal effects of a moon on the planet produce a bulge that is slightly displaced (or misaligned) from a direct line between the two objects. For example, because the Earth rotates faster than the Moon orbits, the Earth-Moon bulge is displaced roughly 3 degrees (and the tide arrives 12 minutes later than we’d expect based on the Moon’s position). This in turn means that the resulting gravitational field of the Earth is deformed into an elliptical shape that includes this misalignment. Mathematically, because the tidal force results from variations (derivatives) in the gravitational potential, the misalignment produces a tidal force of the Earth on the Moon that acts at an angle, inducing a rotation—we call this a tidal torque. Conceptually, we can think of this as in panel 5 in Figure 1; i.e., when the planet spins faster than the moon orbits (so the bulge is carried ahead of the moon), the bulge attracts the moon and the moon attracts the bulge, causing the moon to orbit faster and the planet to slow its spin. In sum, this results in the following: if a moon orbits faster than its planet spins, the torque spins up the planet and this transfer of angular momentum draws the moon’s orbit in closer. The opposite happens when the moon orbits slower than the planet’s spin. However, this interaction is not limited to the moon-planet system: one can also make a similar argument for the effect of the star’s gravitational tides on the planet’s spin and thus the moon’s orbit (e.g., there is an additional tidal effect as displayed in panel 4 of Figure 1).
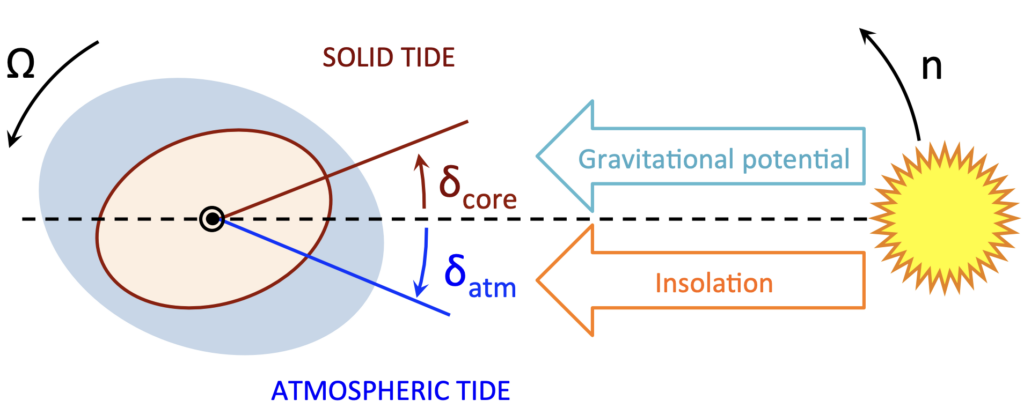
Today’s author then adds a third wrinkle to these two gravitational tidal processes: the effect of atmospheric tides. If a planet has a sufficiently thick atmosphere, the atmosphere will be heated by incident radiation from the star in a process known as insolation (see Figure 2). The variations in the heating rate between different sides of the planet and the heat transfer between different layers of the atmosphere drive winds and circulation of the atmosphere. Then, interactions between the dense, lower layers of the atmosphere and the surface of the planet (which, to a rough approximation, will rotate together) produce a torque that alters the planet’s spin. In fact, such a mechanism has been invoked to explain why Venus rotates opposite to its orbital direction, unlike the rest of the planets! Importantly, the atmospheric tides work in the opposite direction to the gravitational tides. See Figure 2 for a cartoon example of the gravitational and atmospheric torques induced by the host star on a planet. Taken together, these three effects—the gravitational tides of the moon on the planet and the star on the planet and the atmospheric tide—regulate the evolution of the planet’s spin and therefore drive the evolution of the moon’s orbit.
Setting up the equations for the evolution of the moon’s orbit and the planet’s spin with the above three processes, today’s author solves for the behavior of various moons over time. In Figure 3, today’s author only considers the gravitational torques to build intuition, starting with a system that models the Earth-Moon-Sun configuration. Beginning with the moon in the upper left corner of the Figure (where the orbital semi-major axis, x, is small and the planet’s spin, y, is large), the author demonstrates that over time the planet spins down and the moon begins to spiral inward as it reaches the synchronous orbit line—where the planet orbits the sun at the same rate as it spins. As they decrease the semi-major axis of the planet (colors going from black to green to blue), this evolutionary track accelerates, with the moon eventually spiraling into being tidally torn apart by the planet (in the smallest planetary orbits, the moon eventually gets close enough that the tidal force from the planet is stronger than its own self-gravity and it is destroyed in a tidal disruption event).
With this picture in mind, the author then adds in the effects of atmospheric tides, shown in Figure 4 for the same configuration as the green line in Figure 3. Because the atmospheric tides act opposite to the gravitational tides, their inclusion introduces new equilibrium behaviors. In the green and blue lines in Figure 4, the atmospheric tides drive the moon to spiral outward, rather than turning in towards the planet as before (black line), with the effect being more pronounced as the efficiency of the atmospheric tidal force increases (increasing Q). This means that some moons may ultimately be unbound and escape the gravitational influence of their host planet!
Catch me if you can
While modeling this behavior is interesting, this does not solve the problem of observability. In some sense, an escaping moon makes the task of observability with conventional techniques even more challenging. However, today’s author takes the analysis one step further, modeling what happens to these moons after they become unbound. When a moon becomes unbound as in these scenarios, it transitions to an orbit around the host star with roughly the same semi-major axis as the old host planet, meaning that the two will likely meet again. Integrating the orbits of various different unbound moons, today’s author finds that such a reunion is often contentious and ultimately catastrophic—the ejected moons all ended up colliding with the original host planet!
These collisions will likely produce debris, which then quickly becomes dust that works to absorb and reprocess starlight at redder wavelengths. This is usually termed an infrared excess and is common in young planetary systems, when there is lots of dust and collisions. However, as the stars age, such excesses are much rarer and indicate the presence of some other collisional, dust-producing process. Therefore, observing an infrared excess around an older star could be a signature of such a scenario: a terrestrial planet moon evolves to become gravitationally unbound but eventually collides with the host planet, producing a cloud of dust at later times in the star’s life!
Astrobite edited by Evan Lewis
Featured image credit: Composite from Marcin Wichary and NASA