One Plot to Rule Them All – A Review of the Skumanich Law

Title: Time Scales for Ca II Emission Decay, Rotational Braking and Lithium Depletion

Author: Andrew Skumanich

First Author’s Institution: High Altitude Observatory, National Center for Atmospheric Research

Status: Published in the Astrophysical Journal [open access]

Introduction

Gyrochronology — the study of deriving stellar ages from their rotation periods — is a relatively new subfield in astronomy, but has already greatly progressed our knowledge of stellar physics. This bite focuses on the first observations of this idea, published by Andrew Skumanich in 1972. Since then, the paper has garnered over 1500 citations, and even has a dedicated conference for the subfield. Summarized below are the paper’s three main findings.

Lithium Depletion

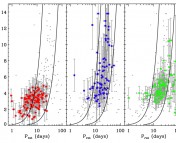
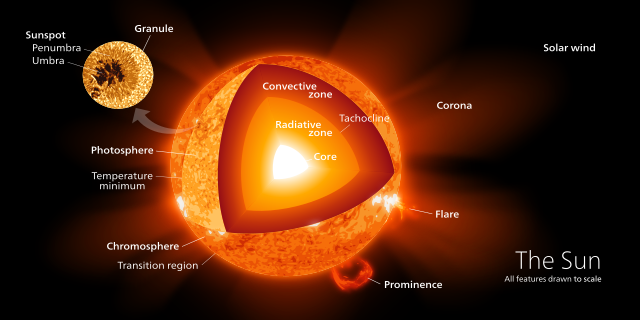
The first conclusion of this paper is in regards to lithium in stars. The lithium abundance of the stellar surface originates from the lithium content of the molecular cloud from which the star formed. The outer convective layer is cooler than the inner radiative layer, so the temperature in the outer layers isn’t hot enough to destroy the lithium in that region (see Figure 2 below for a visual of the stellar structure). However, during the first dredge-up phase (which happens when a main-sequence star evolves to a red giant), the convective layer expands to other layers, thereby mixing with the inner, hotter, radiative core and exposing the lithium to high enough temperatures to destroy the lithium. Therefore, as a star evolves into a red giant, we would expect the star to decrease in lithium abundance. Skumanich observed this in his sample, where the oldest object had the least amount of lithium. This relationship between lithium and age is modeled as and shown as the top curve in Figure 1.

Rotational Velocity

The next conclusion of the paper describes the rotational velocity of stars over time. All stars are born rotating due to the angular momentum of the protoplanetary disk in which they are formed. Once fusion turns on, stars spend most of their life on the main sequence burning hydrogen into helium in their cores. When the star begins to run out of hydrogen in its core, it expands to become a red giant. Throughout these stars’ lifetimes, they experience spin down, where their rate of rotation slows down when their magnetic field interacts with their stellar winds, causing the star to lose mass and slowing its rotation; the magnetic field therefore acts as a brake. This phenomenon is referred to as magnetic braking. In the paper, Skumanich observed evidence of this by measuring the rotational velocity of three objects — the Hyades, the Sun, and field stars in Ursa Major — with different ages. This is shown by the middle curve in Figure 1. He then derived a relationship between the rotational velocity () and age () to be .

Calcium+ Emission

The final finding of this paper pertained to Calcium emission in stars. Due to the small size of stars, stellar surfaces are spatially unresolvable, making it difficult to observe chromospheric activity (i.e. activity in the lower regions of the Sun’s atmosphere, just outside the photosphere; see Figure 2). However, by studying the surface of the Sun, we see two intense lines in the violet part of the visible spectrum referred to as the Calcium H & K lines. These strong lines, which can be observed with ground based telescopes, are indicative of strong stellar magnetic activity; in fact, the Wilson H&K project sought out to measure Calcium H & K lines in solar-like stars to study stellar activity. Skumanich’s paper analyzed this activity as a function of stellar age, and noticed that Calcium emission, and hence magnetic activity, decreases as a star ages. This relationship between Ca and age is modeled as and is shown by the bottom line in Figure 1.

Discussion

Thanks to this one paper, Skumanich provided a relationship to connect a star’s age to its lithium content, rotational velocity and Calcium emission. In summary, 

It is worth noting that since Skumanich’s paper, these relations have been greatly revised to include more data, and incorporate other complicated stellar physics. 

Stellar Ages

This paper’s findings had an incredible impact on stellar physics, especially in determining stellar ages. The age of a star is difficult to calculate. If the star is part of a cluster, one could plot stars on a colour magnitude diagram, fit isochrones to the distribution, and empirically determine the age. But this method requires that the star be part of a cluster, and breaks down for field stars. However, Skumanich’s paper gave us another tool to determine age by using the star’s rotation period.

While age is one of many properties of a star (other properties include mass or metallicity), it is the only property that allows us to study stellar evolution – and on a larger scale galaxy evolution – as a function of time. Without knowing a star’s age, it is difficult to fully understand the lifecycle of a star. 

We’re often taught that it’s rude to ask people their age. But when it comes to stars, astronomers are desperate to talk about ages.

Edited by: Abigail Lee 
Featured image credit: NASA/GSFC/STEREO