Gravitational Lensing Unveils an Ultramassive Black Hole In the Heart of Abell 1201

Title: Abell 1201: Detection of an Ultramassive Black Hole in a Strong Gravitational Lens

Authors: James. W. Nightingale, Russell J. Smith, Qiuhan He, Conor M. O’Riordan, Jacob A. Kegerreis, Aristeidis Amvrosiadis, Alastair C. Edge, Amy Etherington, Richard G. Hayes, Ash Kelly, John R. Lucey, Richard J. Massey

First Author’s Institution: Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham, DH1 3LE, UK

Status: Published in Monthly Notices of the Royal Astronomical Society [open access]

Lurking in the center of nearly every galaxy in the universe there is thought to be a supermassive black hole (SMBH), co-evolving with and influencing the dynamics of its host galaxy. But despite their massive influence and supposedly ubiquitous presence, modeling their masses can be extremely difficult for all but the nearest or most active galaxies. In today’s paper, a team of researchers employed a seldom-used technique for modeling the mass of a galaxy’s central SMBH known as strong gravitational lensing, and as a result may have found one of the largest black holes ever discovered, weighing in at a whopping 32.7 billion solar masses. For reference, there are less than 10 other known black holes thought to be more massive. Their work, beyond just producing evidence of this astonishingly large “ultramassive” black hole, explores the role that strong gravitational lensing may play in future surveys of black hole populations. As it turns out, such methods may help us learn about the relation between black hole mass and host-galaxy mass much further back in cosmic time than is currently possible.

The Why and How of Black Hole Mass Measurement

The idea that galaxies and their central SMBHs co-evolve is relatively new, but has become a central feature of galactic evolution models. This is not due to their direct effect on the gravitational dynamics of galaxies, which is thought to be miniscule, but is rather thought to be related to the ways such SMBHs can accrete and eject gas and stars in the central region of a galaxy, forming what are known as active galactic nuclei (AGN). As a result of this new paradigm in cosmology, studying the relation between the properties of central SMBHs and their host galaxies has become more important than ever. One of the most important relations currently studied in this field is the black hole mass versus host galaxy mass relation, as these parameters seem to be tightly correlated. But how do we actually infer these parameters, and where might our current methods fall short?

Galaxies, owing to their large and luminous profiles, can have their masses estimated in a variety of (conceptually) straightforward ways; one common method involves measuring all the light coming off of a galaxy and equating this luminosity to an underlying mass, which (very roughly speaking) works because we can estimate the light output of stars of a given mass. Another method involves examining the spectra of light emitted from different parts of a galaxy. The shifting of light spectra due to the velocity of stars, known as redshifting or blueshifting, allows us to infer the rotational velocities of certain galaxies, in turn giving an indirect measure of their total mass content. The typical range (specifically the standard deviation) of velocities across a galaxy is known as its velocity dispersion, often denoted $\sigma_{e}$ , and physicists will thus often focus specifically on the $M_{BH}-{\sigma_{e}}$ correlation in their studies (where $M_{BH}$ denotes the mass of the central black hole, and ${\sigma_{e}}$ denotes the velocity dispersion of the host galaxy, often used as a proxy for its total mass).

SMBHs, on the other hand, are exceedingly tiny relative to their host galaxies, and as their name suggests, are rather dark. Thus, measurements of their masses requires either observing the dynamics of objects moving close to them like stars, or observing the reverberation of signals as they travel through the dense gas of an AGN. The former method requires high resolution imagery or spectroscopy, limiting its use to local galaxies, while the latter requires that central SMBHs are “active”, introducing a bias towards measurements of a particular subset of all central SMBHs. If we want to build a full picture of the $M_{BH}-\sigma_{e}$ relation throughout the history of the universe, we need to measure these parameters for galaxies much farther away (and hence further back in time), while also trying to avoid selection biases like these as much as possible.

Figure 1: (Left) HST imagery of the target galaxy within Abell 1201. The close alignment between the target galaxy and the background galaxy causes a strong gravitational lensing effect wherein the background galaxy appears as a distorted arc and also as a small counter image even closer to the target galaxy. (Center) The same image after software removal of the light from the target galaxy, allowing the lensed galaxy to be seen in isolation. (Right) The expected appearance of the background galaxy before lensing, as reconstructed using the most-likely lens model produced in this paper’s analysis. (Adapted by me from Figures 1 and 2 in today’s paper).

In today’s paper, Nightingale et al. employ a less common method in this particular field: modeling the central SMBH’s gravitational lensing of its environment. As described in many previous Astrobites articles, gravitational lensing is a prediction of general relativity (GR) in which extremely massive systems can bend the path of light-rays from background objects like a traditional optical lens, ultimately distorting their appearance. While gravitational lensing is used to model the mass distributions of large systems like galaxy clusters, it can be more difficult to observe lensing due to black holes alone, as their smaller size means their lensing effect is pronounced (“strong”) only for objects extremely aligned with the black hole. In fact, this new work provides the very first complete estimation of a galaxy’s central black hole mass using strong gravitational lensing. Such a discovery was made possible by the particular circumstances surrounding their target object: the brightest cluster galaxy (BCG) within the galaxy cluster Abell 1201. This BCG happens to be aligned with a background galaxy which is distorted to appear both as a large arc around 2 arcseconds away from the BCG, and also as a smaller counter-image only 0.3 arcseconds away.

Bayesian Beliefs about our BCG

So how exactly did they go about their analysis? Using high-resolution imagery from the Hubble Space Telescope (HST) of their target in both visible and ultraviolet light, the team set to work on fitting various models to their data. Given their image, the team needed to know what underlying distribution of mass and light would be most-likely to reproduce both the distorted arc and the small counter-image. To calculate this “likelihood”, they employed a technique known as Bayseian model comparison, which incorporates not only how well a given model fits the data, but also penalizes models which require tuning more parameters—essentially a more rigorous version of “Occam’s Razor”. Each model incorporated different parameters based on whether it included a central black hole, how many light-profiles and mass-profiles were used to model the lens galaxy, the separation of matter and dark matter, etc. By comparing the “Bayesian evidence” of each model, the authors could directly compare how well they fit the data. For those interested in learning more about this process, the authors even provide a Jupyter notebook which explores how to perform strong lens modeling.

Figure 2: Simulation of lensed source using a model without (left) and with (right) and central SMBH at $10^{10}$ solar masses. The top two panels indicate that the inclusion of a SMBH has essentially no effect on the large arc, while the bottom two zoomed-in panels demonstrate how the inclusion of a SMBH affects the counter-image. Thus, the presence of the counter image allows a sensitive test between SMBH models and non-SMBH models. In their analysis, the inclusion of a SMBH matched the real data better in nearly all cases. (Figure 3 in today’s paper).

Figure 2: Simulation of lensed source using a model without (left) and with (right) and central SMBH at $10^{10}$ solar masses. The top two panels indicate that the inclusion of a SMBH has essentially no effect on the large arc, while the bottom two zoomed-in panels demonstrate how the inclusion of a SMBH affects the counter-image. Thus, the presence of the counter image allows a sensitive test between SMBH models and non-SMBH models. In their analysis, the inclusion of a SMBH matched the real data better in nearly all cases. (Figure 3 in today’s paper).

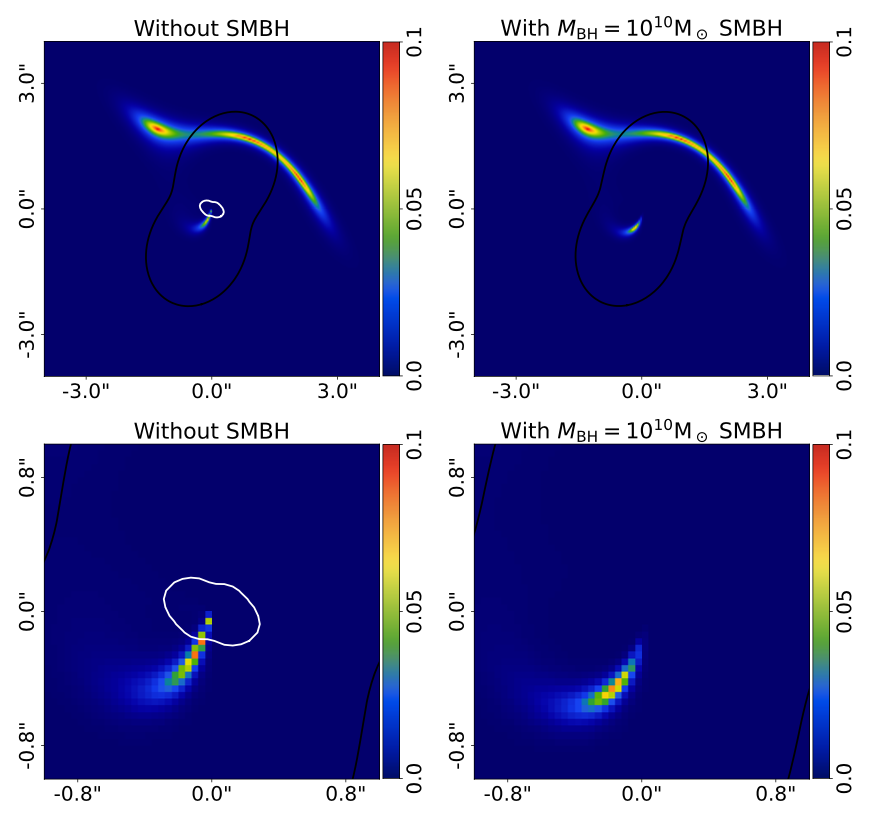
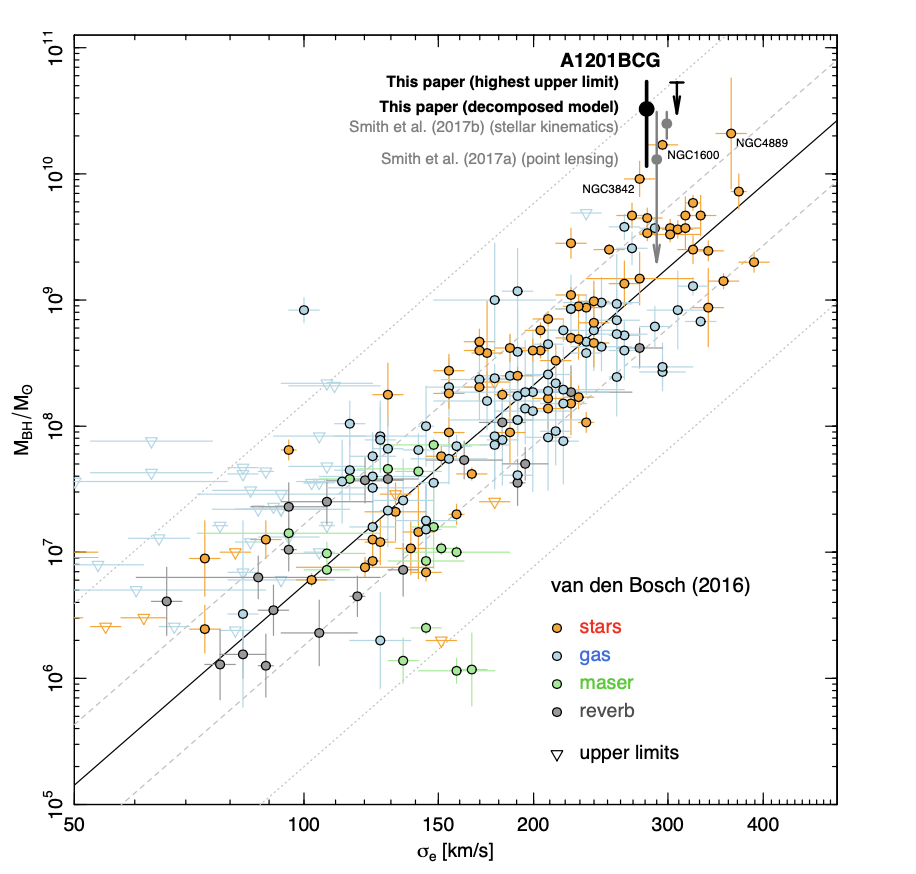
After performing their analysis, the research team found that in three out of the four main mass-profile models, the addition of a central black hole was greatly favored by the evidence. The one model in which the presence of a central black hole was not favored also required that the galaxy’s peak mass be offset from its peak luminosity by over 100 parsec, and so the authors considered this result unphysical. Upon receiving this evidence for a central black hole, it makes sense to ask: what black hole mass gives us the best agreement with our observations? In examining this question, the team explored the range of probable masses for their three main models, and found that they all estimate the mass of the central black hole to be within about 20-40 billion solar masses. Upon combining the probability distributions of each model, they quote a final predicted mass of $3.27\pm2.12\times10^{10}$ billion solar masses, putting this particular galaxy’s black hole mass in the extremely rare “ultramassive” range.

In the context of the aforementioned black hole mass versus host galaxy mass question, this result contributes to a small set of super- or ultra- massive black holes that are known to exist within the highest velocity-dispersion (and therefore highest mass) galaxies. Interestingly, many of these galaxies are 1.5 $\sigma$ -2.0 $\sigma$ higher than is expected given the mass of their host galaxies (where $\sigma$ denotes one standard deviation), whereas there are no known central black holes that are more than 1.5 $\sigma$ below the expected mass. Whether this is due to a real physical effect or is simply a statistical fluke is still unknown.

Figure 3: A plot of the $M_{BH}-\sigma_{e}$ relation as surveyed in Bosch (2016), with the new result from this paper added in (the black data points in the upper right). Given the velocity dispersion of the target galaxy denoted here as A1201BCG, the mass estimate in this paper puts the galaxy ~2 $\sigma$ away from the expected trend-line. The authors note that the presence of multiple excessively massive central SMBHs in this part of the graph without any corresponding low-mass outliers may indicate a break from the linear trend, but there is not enough data to make any firm conclusions yet. (Credit: adapted by the authors from Bosch 2016, figure 12 in today’s paper).

Figure 3: A plot of the $M_{BH}-\sigma_{e}$ relation as surveyed in Bosch (2016), with the new result from this paper added in (the black data points in the upper right). Given the velocity dispersion of the target galaxy denoted here as A1201BCG, the mass estimate in this paper puts the galaxy ~2 $\sigma$ away from the expected trend-line. The authors note that the presence of multiple excessively massive central SMBHs in this part of the graph without any corresponding low-mass outliers may indicate a break from the linear trend, but there is not enough data to make any firm conclusions yet. (Credit: adapted by the authors from Bosch 2016, figure 12 in today’s paper).

Cosmic Reflections

Returning back to the bigger picture, this work provides the first complete estimation of a galaxy’s central SMBH mass using strong gravitational lensing, a method which doesn’t require the presence of an AGN or confine our observations to local galaxies. In this way it outlines a possible future method for exploring the $M_{BH}-\sigma_{e}$ relation across cosmic time, which would greatly help astronomers and physicists trying to understand galactic evolution. However, the authors caution that the particular circumstances that allowed this analysis to be performed in the Abell 1201 system may not be common in nature, so it is yet to be seen how fruitful this method will be in the future. Regardless, it’s safe to say that this paper constitutes quite an (ultra)massive discovery.

Astrobite edited by Evan Lewis

Featured image credit: Nightingale et al. 2023

About the Author

About Lucas Brown

I'm a current master's student at Tufts University interested in cosmology, relativity, and gravitational physics. I am currently doing research on the stochastic gravitational wave background and pulsar timing arrays. Outside of physics I love playing piano, climbing, and spending time with my dog.

Gravitational Lensing Unveils an Ultramassive Black Hole In the Heart of Abell 1201