Title: Black-hole mergers in disk-like environments could explain the observed q−χeff correlation
Authors: Alessandro Santini, Davide Gerosa, Roberto Cotesta, and Emanuele Berti
First Author’s Institution: Universita degli Studi di Milano-Bicocca, Milano, Italy
Status: Submitted to Arxiv [Open Access]
First Position
Have you ever looked at a supermassive black hole and thought “Gee, this is great and all, but what I would really love is more black holes.” If so, you and today’s authors have something in common. They consider the scenario where black holes merge in the accretion disk around an active galactic nucleus (AGN). Most galaxies have a supermassive black hole at their center (yes, even our own) which tend to form disks of extremely hot matter as gas and dust spiral into their eventual gravitational demise. An AGN is a central supermassive black hole whose accretion disk is so energetic that it outshines its entire host galaxy.

The thought of black holes nestled in the AGN accretion disk is not new, but today’s authors consider it in light of a specific question: Can this spinning environment explain a strange phenomenon observed in black hole merger spins? Specifically, LIGO data has shown that the more uneven a pair of black holes are in mass when they merge, the greater their effective spin. This heretofore unexplained phenomenon is the subject of today’s astrobite: Can adding a rotating dance floor (the AGN accretion disk) explain the strange pattern in spins of a black hole merger ballet?
Pas De Deux
In order to talk about this phenomenon and black hole mergers in general we need to talk about spin, which in physics we describe through angular momentum, usually represented with a capital L. In a binary black hole merger, there are two kinds of angular momentum at play: the angular momentum of the black holes around each other as they spiral inward (called the orbital angular momentum, the do-si-do in my forced dance analogy) and the angular momentum of each black hole itself as it spins (the pirouette in my still forced dance analogy). Like regular momentum, angular momentum is conserved, so the resulting combined black hole will have a spin angular momentum equal to the sum of the 3 angular momenta that went into making it (2 spins and 1 orbital).
Astrophysicists decided that keeping track of these 3 different black hole angular momenta as they merged was simply too much work, so they chose to describe them all with a single number, called the effective spin. The effective spin is basically a weighted average of the 2 black hole spins relative to the orbital motion, where the average is weighted by the mass of the black holes. For example, if both black holes are spinning clockwise, and they are also orbiting each other clockwise, the effective spin will be near 1, see the fourth diagram in Figure 2. If they are both spinning counterclockwise and the orbit is clockwise, the effective spin will be near -1. If the black holes are spinning in opposite directions, the effective spin will be closer to zero, see the third diagram in Figure 2.
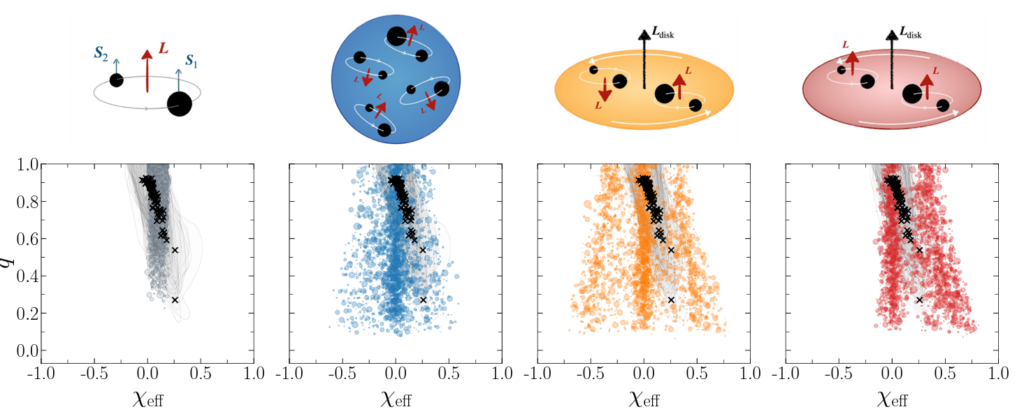
This effective spin, χeff, is the parameter that revealed the strange trend in LIGO data. The variable q is defined as the ratio of the masses of the black holes, and as q decreases (the masses become more uneven) χeff increases, which was unexpected to astronomers. The authors of this paper set out to determine how this can be explained. They point out that it has already been shown that mergers with more uneven mass ratios (higher q) tend to come from hierarchical mergers in dense environments. Hierarchical mergers occur when 2 black holes merge and then the new, bigger black hole formed goes on to merge again, and the process continues, creating a bigger and bigger black hole. The authors then pointed out that the accretion disks around AGNs are a promising location for these types of mergers, thanks to a phenomenon called migration traps, where essentially the fluid dynamics of the disk create areas where black holes will tend to congregate and merge. On top of all this, the accretion disk itself is spinning. This spinning causes black holes in the AGN disk to prefer to spin either in the same direction (aligned, see the rightmost diagram in Figure 2) or the opposite direction (anti-aligned, see the left black hole merger of the third plot of Figure 2) of the disk. This again is fundamentally due to the conservation of angular momentum, but you can also see it in our solar system. All of the planets rotate in either the same direction as their orbit or in the exact opposite direction (Uranus and Venus are the only ones to spin in the anti-aligned direction), but not in some random direction at a weird angle to the orbit. Therefore, the black holes in our accretion disk will prefer to be in these aligned or anti-aligned directions, and the authors hypothesize that this could be causing the correlation we observe.
Corps de Ballet
To test this hypothesis, the authors turned to computer simulations made of two sets of black holes. 20% of the black holes would undergo hierarchical mergers in an AGN disk, and thus have their spins fixed to either aligned or anti-aligned to the disk spin. The other 80% of the black holes would be more isolated binaries sitting outside the disk in the galactic field, and hence have no preferred direction, like plot 2 in Figure 2. The authors gave each type of black hole a mass based on a power law distribution and picked the number of times that a black hole in the disk will undergo hierarchical mergers from a Poisson distribution. This way, some black holes undergo more mergers than others, as they would in the real universe. Plugging all these parameters into a numerical relativity simulator (i.e. a computational program that can handle general relativity rather than Newtonian gravity) the authors were able to extract a hypothetical distribution for q versus χeff for these simulated black hole mergers.
The authors find a correlation similar to the one in the real data, and argue that their model, at least qualitatively, reproduces the observed correlation! You can see this in Figure 3.
Finale
The authors go very far out of their way to note that the model only agrees with the data qualitatively, i.e. they both exhibit similar behavior but not necessarily exactly the same trends. This could be an indication that the spinning environment around an AGN could be forcing black hole spins into alignment or anti-alignment, causing the observed trend in the data. However, the authors highlight the several simplifying assumptions they made in constructing this model. They didn’t do any sort of numerical fit to the data, only chose some reasonable values for their parameters and checked the resulting distribution. They also neglected to investigate many parameters for the sake of simplicity, such as redshift or total mass, which could be important in determining correlations. However, the authors want to make extremely clear a major qualitative conclusion: the resulting correlation is observed even if one doesn’t require that the black hole spins be exactly aligned or anti-aligned to the disk’s spin. Running the model again where the spins are only close to being aligned or anti-aligned yields the same qualitative results. This is a very promising sign for the model, as the spins not being perfectly aligned is a much more realistic scenario, meaning the model is a better match to the real universe. Thus, the authors urge follow-up with a more rigorous approach to extend this idea that they began experimenting with.
Why should we care about what causes this bias at all? The authors point out that if the relationship can be proven, i.e. we can demonstrate spinning disk environments cause this bias, then we can use it in the future to infer what environment black holes are in. Thus, if we see a population of black holes with a similar bias, it may be eventually possible to work out the properties of their surroundings! The analysis of binary black hole mergers through gravitational wave data is an extremely new field and already is giving us new insight into some of the most extreme environments in the universe. Only time will tell what will be uncovered as we continue to dive deep into LIGO and VIRGO data!
Astrobite edited by Yoni Brande
Featured image credit: Wikimedia Commons