Title: The Pedagogical Representation of Mass Functions with LEGO and their Origin
Authors: Stefan J. Kautsch, Dimitri Veras, Kyle K. Hansotia
First Author’s Institution: Department of Chemistry and Physics, Halmos College of Arts and Sciences, Nova Southeastern University, Fort Lauderdale, FL 33314, USA
Status: Published in European Journal of Physics [open access]
How is the Universe like a box of LEGOs?
Throughout the cosmos, little things far outnumber big things. In the asteroid belt, petite pebbles dominate over big boulders, just as smaller rocky planets are more prevalent than giant Jupiters. In our Milky Way, low-mass stars monopolize the stellar population, with the biggest and brightest constituting a small minority. Grand galaxies like Andromeda are rare compared to dwarfs like Sagittarius. These hierarchies tie our Universe together, constructing a cascading connection from the smallest scales to the absolute largest.
Mathematically, each of these astronomical hierarchies are remarkably similar. If we were to choose one of these systems — say, a population of stars — and make a histogram of the masses of the constituent bodies, we’d find that the shape of this histogram closely resembles that of other systems — like clusters of galaxies — on completely different scales. These histograms are broadly referred to as mass functions (see, e.g., this Astrobite and this Astrobite). In nearly every case, these mass functions take the shape of power laws, where the number of objects of a given mass is proportional to the mass raised to a constant power. The constant exponent is known as the power law index or power law slope and dictates the proportionality of bigger objects to smaller objects; if the power law index is -2, for example, this means that each time we cut the mass in half, the abundance of objects with said mass is quadrupled (i.e., multiplied by (½)-2 — as illustrated in Figure 1).

While mass functions might seem mundane, they’re packed with information. Mass is an incredibly important property for many astronomical objects — mass influences the habitability of planets, the lifetime of stars, and the structure of galaxies; thus, knowledge of the distribution of masses within a population is vital. Additionally, the change in a mass function over time can teach us how certain objects evolve, like the stars within a star cluster or within a whole galaxy.
But, like most things in astronomy, these mass functions are intangible. Sure, we can read in a textbook that stellar masses follow a power law, or we can even fit a curve to a sample of data, but we can’t actually reach out and hold these stars and weigh them and sort them into bins ourselves. As such, today’s authors propose a creative way to build physical intuition for mass functions: follow the LEGO brick road.
Building a mass function, brick by brick
Like most astronomical objects, LEGOs come in many shapes, sizes, and masses. Therefore, given an arbitrary LEGO set, one can straightforwardly piece together a LEGO mass function! While today’s authors use the “garmadon, Garmadon, GARMADON!” LEGO set (since it contains a shark model resembling their university’s mascot), any LEGO set should work for this experiment.
The authors sort the LEGO pieces by shape and by color and then used a lab-grade scale to measure the mass of one representative brick from each sorted group; assuming mass differences between bricks of a given group are negligible, one only needs to know the number of bricks in that group (listed in the instruction manual) to compute the total mass of the population. Each mass is measured three times and the values are averaged to reduce measurement error. The authors then construct a histogram of brick frequency vs. mass, choosing to use six equally wide mass bins, since this bin spacing gives the best fit to a power law.
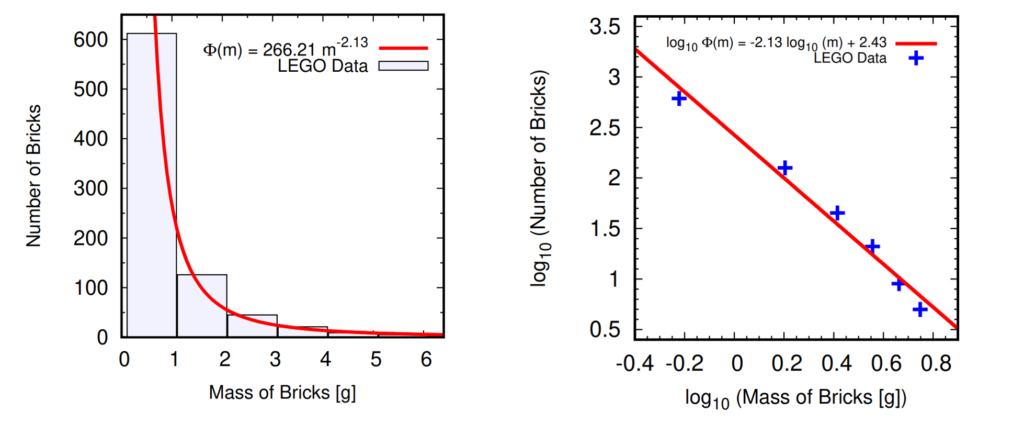
The authors find that a power law fits their data quite well, as shown in Figure 2; the fitted power law index of -2.13 has a standard error of 0.16, or a percent uncertainty of only 7.5%! The fit isn’t perfect — and could be improved by using a “broken” power law instead, where the low-mass data is fit with a different index than the high-mass data — but the errors are low enough to consider this experiment a success.
Piecing together a pedagogical payoff
The authors’ LEGO experiment is ideal for a classroom demonstration or for an independent lab assignment. Not only does this experiment provide hands-on, physical intuition for what a power law or a mass function actually looks like, it also demonstrates a number of key concepts in statistical analysis. By repeating the experiment with different random samples of LEGO pieces, one can examine selection bias — how does the sampling procedure affect the final results? In measuring the masses of the bricks, questions of measurement uncertainty naturally arise — how can one minimize error in the way the data is collected? And, in fitting a curve to the data, one must think critically about model selection — is a smooth power law really the best fit to the data, or would another curve be more appropriate? All of these questions have implications in quantitative fields far beyond astronomy.
The concept of a power law is also widely applicable. Yes, by better understanding mass functions we can better appreciate the building blocks of our Universe — how everything is connected, from the smallest dust grains to the largest galaxies. But, this LEGO experiment can also help us appreciate things closer to home. The distribution of biomass on Earth, for instance, follows a power law, with minuscule microbes outnumbering the biggest beasts. The sizes of lakes, the strengths of earthquakes, and even the distribution of wealth follow similar trends. Evidently, LEGOs can teach us a lot about the world — we just need to know how to connect the blocks.
Astrobite edited by: Catherine Manea
Featured image credit: astronomy.com and stock.adobe.com




Thanks, interesting post. From Cephalopods and Sunflowers to stars and galaxies, math rules.