Title: Disentangling the Black Hole Mass Spectrum with Photometric Microlensing Surveys
Authors: Scott Ellis Perkins, Peter McGill, William Dawson, Natasha S. Abrams, Casey Y. Lam, Ming-Feng Ho, Jessica R. Lu, Simeon Bird, Kerianne Pruett, Nathan Golovich, George Chapline
First Author’s Institution: Lawrence Livermore National Laboratory, 7000 East Ave., Livermore, California 94609 USA
Status: submitted to AAS
Lonesome Black Holes
Seeing the darkness is something that is a great mystery in modern physics, from dark matter to black holes. How do you see something that doesn’t emit light?
Current methods of detecting black holes include observing their accretion from surrounding matter, whether that’s supermassive black holes in the centre of galaxies, or black holes which are stealing matter from a stellar companion. Black holes which don’t have any glowing surrounding matter may have a black hole or neutron star partner to spiral into, releasing gravitational waves which we detect with LIGO, Virgo and KAGRA detectors. But lonely black holes sitting in the darkness are significantly harder to uncover. In the Milky Way, it’s expected that there are 100 million isolated and binary black holes that are born from dead massive stars. Of those, only ~50 black holes in binaries have been detected.
Twinkling lights
Fortunately, there’s a detection method that can fill this gap: microlensing. If an isolated black hole is located in front of a star or galaxy much further away, that background object’s brightness will vary with time as the light is lensed by the black hole moving in front of it. This is similar to a magnifying glass passing the star’s tiny pinprick of light, but instead the lens of the glass is the curvature of spacetime bending due to the black hole. Because of the magnification of the background object by the lens, it will appear to change in brightness, twinkling like fairy lights.
However, there are a few different kinds of objects that can microlens background stars. Black holes, white dwarfs, neutron stars, and free floating planets have all been found through microlensing. If we can know the mass of the lens, then we can more obviously characterise a lens as a black hole (usually 5-100 times the mass of the sun), but an individual microlensing light curve doesn’t carry any useful information about the mass of the lens without also knowing the astrometric shift in the lensed object, something we don’t have for many microlensing observations. However, studying a larger group of microlensing events can break the degeneracies present in individual lightcurves and classify lensing events and search for the hidden black holes in the dark. Today’s paper defines a framework for determining the class of individual detections and groups of microlensing events using probabilistic models and Bayesian statistics.
Looking at populations of Black Hole lenses
Different types of lenses will be distributed differently in the effects they create in the light curves that we detect. For example, there will be more black holes over a certain range of masses and more white dwarfs over a different range, this means the distributions of some of the measurements of the lensing profile, such as the angle between the image of the source from the actual source location, will be different because of correlations between these parameters and the lens mass.
This paper looks at 3 potential sources: free-floating planets (FFPs), stellar origin black holes (SOBHs), and primordial black holes (PBHs). Accounting for PBHs in the model separately to SOBHs allows this method to demonstrate a measure of the abundance of PBHs, which could provide an explanation for dark matter or evidence for the first black hole seeds in the early universe. They construct four simulated universes each with the same number of mock microlensing events for FFPs and SOBHs, but each with a different number of PBHs. For each of these universes, the distribution of the distances and the kinematics of the events are the same, but there is a different distribution of lens masses caused by the varying fraction of PBHs.
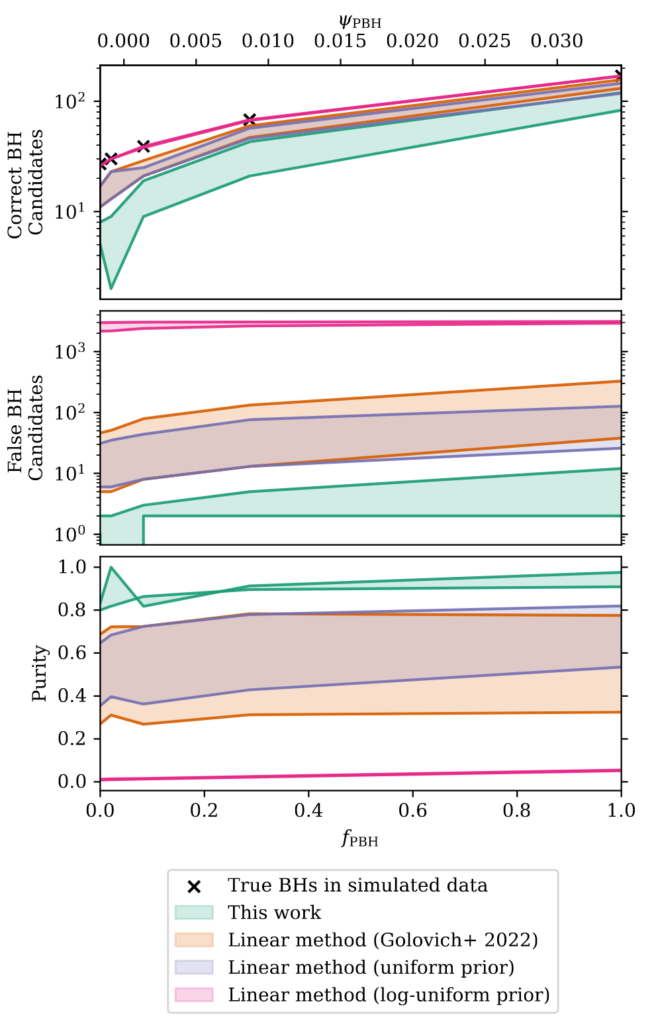
Using these mock events, they construct a probability of events belonging to a certain class for each universe. If you assume a fixed group of certain types of lenses (meaning a fixed mock universe and lens mass distribution), and you know the profiles of the microlensing light curves that are likely to be produced by each of those different lens types, you can say how probable it is that a microlensing event is caused by a specific type of object. Their method reliably classifies most of the true black hole events from each population’s mock events, as shown in Figure 2. While their method has fewer correct black hole candidates, or “true positives”, than previous methods, their identified population of black holes has much fewer false BH identifications, therefore a much higher purity of detection.
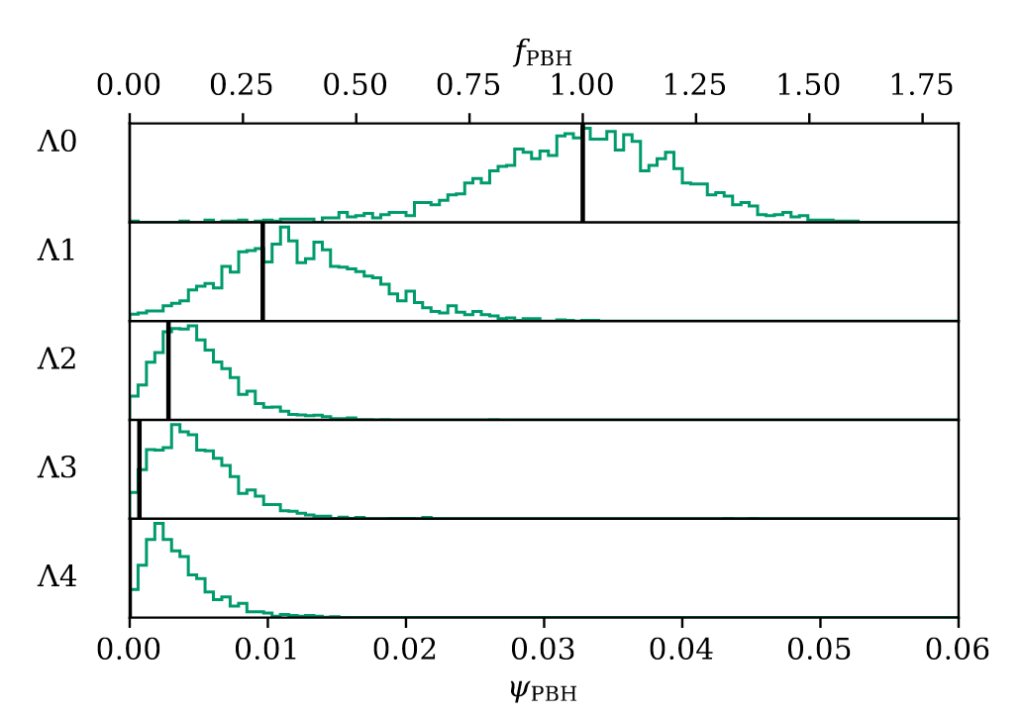
Alternatively, if you have a group of microlensing events and a model for the universe, you can say how probable it is that you are observing events in that universe. When drawing a group of events from their four mock universes, they characterise how well they can recover the fraction of PBHs from these groups of events, as seen in Figure 3. The probability of the fraction of PBHs follows the true value, meaning if there really were lots of PBHs in the Milky Way that match these models well, we could say that PBHs exist with high confidence. If there is a smaller fraction of PBHs, then we would be able to place upper limits on what we can detect.
The future of black hole microlensing surveys
The next step for the authors’ statistical framework is to test it with real photometric measurements for microlensing from the OGLE project, a survey of more than a billion stars for time-domain astrophysics. Combining this method and real observations with more realistic model universes and more sophisticated simulations of PBHs, SOBHs, and other types of lenses, this could tell us more about the BH populations alone in the wild. Pairing these results up with astrometric measurements that will come from the Nancy Grace Roman Space Telescope in the next few years will provide even more knowledge about the kinds of black holes twinkling stars (or fairy lights?!) in the night sky.
Astrobite edited by Samantha Wong
Featured image credit: Jimmy Chan, modified by Storm Colloms




There seems to be a problem with the video.
You might be able to refresh the page and see if that works 🙂
“In the Milky Way, it’s expected that there are 100 million isolated black holes that are born from dead massive stars. Of those, only ~50 have been detected.” Where does the 100 million estimation and the ~50 number of detections come from?
Sorry for the delayed reply Dabed! That’s a great question, and it involves some keen science to make the estimates of number of black holes in the Milky Way. This estimate comes from measuring the density of ‘heavy’ elements in the galaxy. Because we know that the original elements in the universe were mostly Hydrogen and Helium and a tiny bit of Lithium after the big bang, the rest of the elements in the galaxy will have been produced in stars. Past Iron, any heavier elements can’t be made in stars but have to have come from supernovae explosions. These elements will be ejected back into the gas in the universe, and eventually formed into the next generation of stars. If we measure the chemical composition of the gas and the current stars in our galaxy, we can deduce the number of supernovae that have produced that fraction of heavy elements. Given that a certain fraction of these supernovae came from massive enough stars to form black holes, we can use the estimated number of supernovae to get this number of black holes.
I actually made a mistake in this sentence, as we predict the total number of Milky Way black holes to be 100 million, including both isolated and binary (and ternary!) black holes. The number of detected black holes in the Milky Way mostly then comes from black holes observed in x-ray binaries and through eclipsing black holes passing in front of stars. I’ve updated the article to reflect this mistake, thank you for spotting it!