- Title: Weak lensing using only galaxy position angles
- Authors: Lee Whittaker, Michael Brown, Richard Battye
- First author’s institution: University of Manchester, UK
Gravitational lensing is the deflection of the trajectory of a photon by gravity, and it is a natural consequence of the theory of General Relativity. A photon that would normally travel in a straight line bends its trajectory when it passes near a massive object. One of the wonderful things about gravitational lensing is that it helps us understand the properties of dark matter in the Universe. This paper is concerned with a regime called “weak lensing” and with finding new methods to measure this effect.
To understand what we mean by weak lensing, consider the following example. You look at the sky and you see a galaxy. Behind that galaxy, at higher redshift, there is another galaxy, which we will assume that looks just perfectly round as an example. The photons from the background galaxy travel through the Universe to us and along the way, they encounter the foreground galaxy, which deflects them a little bit from their original path. As a consequence, when we see the galaxy in the background, it no longer appears round. Lensing has changed its shape to make it look more elliptical. The picture below shows a slightly more complicated example, where there is an ensemble of background galaxies being lensed by a cluster of galaxies. A cluster is a dense place in the Universe where many galaxies are grouped together with dark matter. Lensing by the cluster makes the shapes of the galaxies in the background look more elliptical around it.
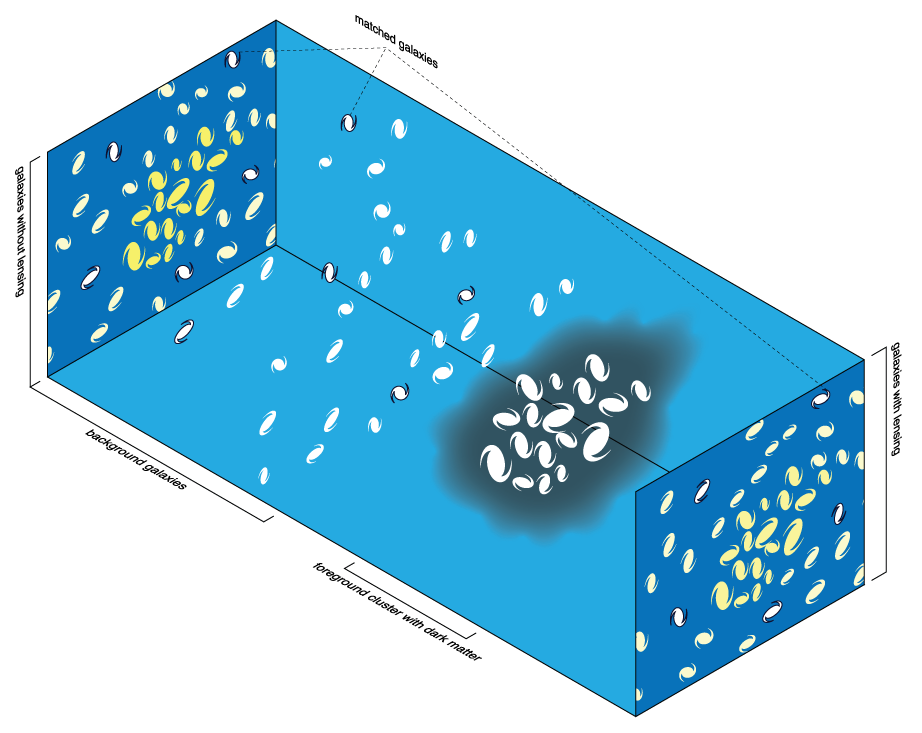
Gravitational lensing by a cluster of galaxies (the black blob). Photons from the galaxies in the background (projected to the left of the figure) are deviated from a straight path, making the background galaxies look more elliptical around the cluster when we see them from the right. You can locate some specific examples in the galaxies with black contours and see how lensing changes their ellipticities and orientations so that they look like they are wrapping around the cluster (projected in yellow).
In the figure above, you can see that because background galaxies change their ellipticities due to gravitational lensing, and because they do so in a preferential direction, they also change the direction in which they are pointing. Typically, in a case as described in the figure above, one would be able to measure the mass of a cluster by measuring the ellipticities of the galaxies in the background. Because lensing is “weak”, many galaxies are needed to obtain an accurate measurement. The authors of the paper propose that we need not measure ellipticities of galaxies, which are very hard to obtain; instead, they suggest that the same information can be obtained from the orientation angles of galaxies and construct a statistical method to achieve this goal. In addition, they suggest that measuring the orientation angle of a galaxy is easier than measuring its ellipticity, which requires a precise calibration and an exquisite understanding of the properties of the telescope that took the image.
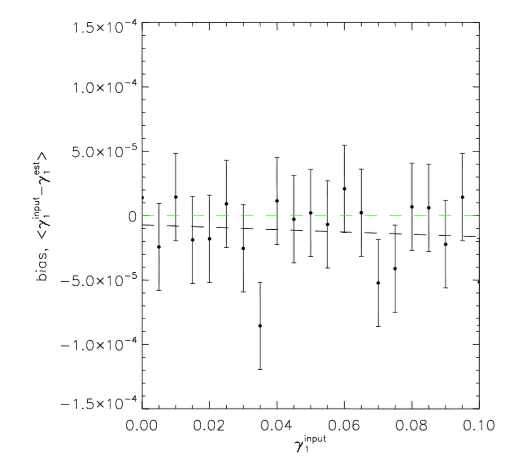
A test of the input shear and the difference between the input and recovered shear. This test shows that the method of measuring galaxy orientations to recover the shear works very well. (Fig. 3 of Whittaker et al.)
To test their method, the authors use both simulations and observations. First, they simulate a set of galaxies that have been lensed. The degree of lensing is described by the “shear”, gamma, which represents the change in the original ellipticity of the galaxy after its been lensed. They simulate galaxies that have been sheared by a known amount and apply their proposed method of measuring orientation angles to retrieve the shear. In the figure to the right, the points are the simulated data. The green line is the ideal result and the black line is the best fit to the points, which is overall consistent with zero within the uncertainties.
The authors also work out some modifications to their method when position angles cannot be measured perfectly. While in this case there is a systematic deviation from the true shear (“noise bias”), it can be accounted for. One important aspect of the method they propose in this paper is that it not only uses position angles, it also requires knowledge of the overall properties of the shapes of galaxies. This means that they need to know how many galaxies there are with a given ellipticity.
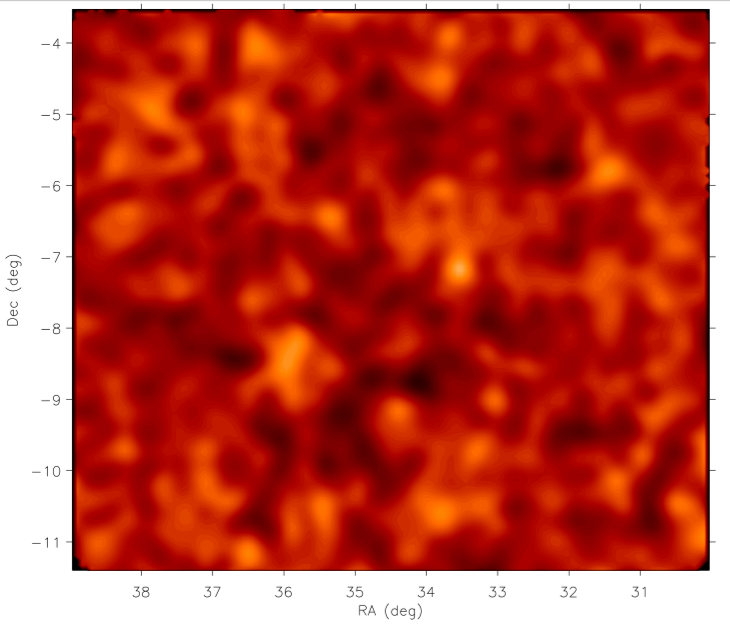
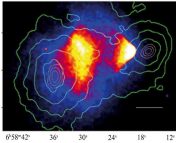
A map of the matter (dark and luminous) that is lensing background galaxies in one of the CFHTLenS fields using the position angle method. Because lensing is due to all the matter, dark and luminous, it helps us understand what the Universe is made of. (Fig. 15 of Whittaker et al.) From black to yellow we go to higher mass densities and more lensing.
Once the method has been validated, they run it on a cosmological simulation, a simulation of the distribution of dark matter in the Universe, and on real data from the CFHTLenS, which maps the ellipticities of galaxies across large areas in the sky (see this astrobite). In both, they attempt to reconstruct the distribution of matter by applying their method and also by applying the more common method of measuring galaxy ellipticities. They find that the two methods are consistent with each other and that the position angle method gives better constraints on the reconstructed matter field. In the case of the data, this amounts to a 20% smaller uncertainties for the position angle method. The figure to the left shows the reconstructed mass density field from the CFHTLenS.
We are at the verge of many interesting applications of weak gravitational lensing. This ability to locate dark matter lets us understand more about the properties of the Universe. In the upcoming years, many telescopes will dedicate a large amount of their time to measure the shapes of galaxies and to map the matter in our Universe. This paper proposes a new method for reconstructing a map of matter in our Universe, by using position angles of galaxies. It is only the beginning.