Title: A New Approach to Observational Cosmology Using the Scattering Transform
Authors: Sihao Cheng, Yuan-Sen Ting, Brice Ménard, Joan Bruna
First Author’s Institution: Department of Physics and Astronomy, The Johns Hopkins University, 3400 N Charles Street, Baltimore, MD 21218, USA
Status: Submitted to arXiv
Neural networks have seen a lot of hype in astronomy and cosmology recently (even just on this site! See these three bites). However, it may be that the neural networks used to classify images in typical machine learning applications are overkill. To quote the authors of today’s paper, “the cosmological density field is not as complex as random images of rabbits.” Today’s authors propose using a method called the “scattering transform” to take advantage of the best parts of neural networks with none of the limitations.
Non-Gaussianity Insanity
The standard cosmological lore states that early on the universe underwent a phase of inflation that is responsible for laying down the initial conditions of the large-scale structure we see in the universe today. These initial conditions were very nearly Gaussian, or white noise like static you might see on old TVs. The fluctuations of this noise produced the initial seeds of structure formation (for more, see these two bites about the Planck CMB analysis). Gravitational evolution caused these seeds to grow, and, eventually collapse into dark matter halos, filaments, and the rest of the cosmic web where galaxies and matter live today. Cosmologists jargon-ize the fact that the cosmic web looks nothing like white noise by saying that the density field today is “Non-Gaussian”, a term that applies to any deviation from Gaussianity.
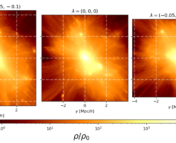
The distinction between Gaussian and Non-Gaussian is important because our standard analysis tool in cosmology is the power spectrum. The power spectrum measures the clustering of matter – or, roughly, how likely it is to find clumps of dark matter separated by a certain distance scale, but it only contains all the information in the density field if the field is perfectly Gaussian. Cosmologists want to squeeze as much information juice out of the cosmic lemon as they can, so they need a way to capture not just the Gaussian information, but also the Non-Gaussian information. The need for this extra information is illustrated in Figure 1, where each row shows an identical power spectrum and the density field it corresponds to, which are clearly quite different. The question then becomes – how to go beyond the power spectrum?
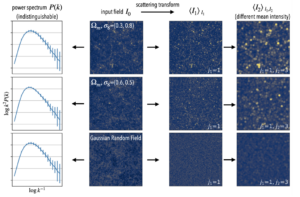
Figure 1: Identical power spectra (first column) for different density fields (second column, with associated cosmological parameters) and the result of applying the scattering transform (third and fourth columns). Figure 3 of today’s paper.
Neural Networks – What’s the big deal?
One way to go beyond the power spectrum is with Convolutional Neural Networks (CNNs) – the kind that sort pictures of cats from those of dogs. CNNs have the potential to extract information that the power spectrum just can’t see – the Non-Gaussianity. Recent applications of CNNs to learn cosmological parameters have shown great potential. Put simply, a CNN learns by guessing a label for an input set of (labelled) training data and comparing it with the true label. That label might be a category (cat or dog) or a cosmological parameter value. By running cosmological simulations where we know the true cosmological parameters, it is possible to train a CNN on the simulated density fields so that when we hand it a new cosmological parameter it gives us the full, Gaussian and Non-Gaussian, density field!
However, CNNs are not without their own issues. Namely, training can be expensive and, more importantly, robustness can be a big problem. Robustness, in this context, means that if the CNN is given an image that is different from one that was in the training set, it may catastrophically fail in classifying it. This is illustrated in Figure 2 for a neural net image classifier (specifically Google’s InceptionV3 trained on the ImageNet dataset) that very confidently misclassifies a slightly altered image of a cat (that was not in its training set) as guacamole! To be fair to CNNs, there are techniques out there to guard against such so-called “adversarial examples” (such as rotating images during training), but this extreme example illustrates that robustness can be an issue with CNNs for data that is even subtly different from the training data.
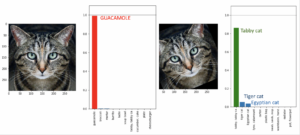
Figure 2: Adapted from the blog by the first author of this paper describing adversarial examples and their challenge to robustness. The y-axis shows the probability that the image belongs to a certain category, some of which are listed on the x-axis. For ease of viewing a horizontal line at probability of 1 and labels have been added.
A Smattering of Scattering
Today’s paper proposes using a different technique to capture Non-Gaussianity, and to do it robustly. This method is called the scattering transform, which is based on the concept of wavelets (kind of like a more general Fourier transform). Without going into the details of the scattering transform, it suffices to say the authors have applied it in such a way that it takes advantage of the fact that the universe is homogeneous and isotropic. The scattering transform has very similar essential features to those of CNNs – it can therefore also access Non-Gaussian information in a similar way. However, this is not a machine learning method in the usual sense – meaning there is no need to train it on data! This fact means the scattering transform doesn’t have to worry about the cosmological equivalent of sneaky guacamole-cats that it didn’t happen to see during training – this is the source of its robustness. The scattering transform is actually an estimator, and is closer to the power spectrum in terms of computational efficiency.
The authors put this method to work in analyzing weak gravitational lensing sky maps to infer the two cosmological parameters Ωm and σ8, which, respectively, describe the amount of matter in the universe, and the amplitude of the power spectrum (roughly how much structure there is). These parameters are typically degenerate in power spectrum analysis, meaning it is hard to constrain both of them using just the power spectrum, which is the workhorse of the standard analysis in cosmology. However, by exploiting Non-Gaussian information, the scattering transform can place tighter constraints on the values of these parameters than the power spectrum can. These constraints are shown in Figure 3, where it is clear that the scattering transform outshines the power spectrum, and also that it performs comparably to the CNN, but comes with the added benefit of robustness!
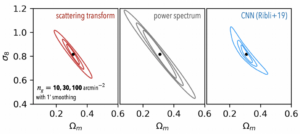
Figure 3: Parameter constraints on Ωm and σ8 using the scattering transform (left), power spectrum (center), and CNN (right). Nested contours correspond to different noise levels added to the data (bottom left). Figure 6 of today’s paper.
The end of neural networks?
Clickbaity title and feline-avocado dips aside, this is not the end for neural networks. However it is a great example of how knowing your problem well can strengthen cosmological parameter constraints without sacrificing robustness to a CNN. With modern cosmologists fretting about several parameter tensions, including the Ωm– σ8“tension“, the ability to extract Non-Gaussian information, and do it robustly, will be crucial to improving our understanding of the universe.