Authors: Marika Asgari, Indiarose Friswell, Mijin Yoon, Catherine Heymans, Andrej Dvornik, Benjamin Joachimi, Patrick Simon, Joe Zuntz
First Author’s Institution: Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
Status: Submitted to MNRAS
Much like Voltron, different observational probes of cosmology are powerful on their own, but are at their strongest when combined together. This power comes from the ability to obtain better constraints by breaking parameter degeneracies, a jargon-y phrase we will unpack the meaning of in today’s bite.
Combination Station
The ΛCDM model – the standard model of cosmology – tells us all about the large-scale distribution of matter in the universe with just 5 parameters. However, we cannot directly measure the matter distribution directly since it is dominated by dark matter which produces no observable signal. Instead we have to turn to tracers of the dark matter, or observational probes. One such tracer is gravitational lensing of light from some background source by matter between us and the source. Another is the positions of galaxies themselves and their clustering. Whereas the lensing signal is a direct tracer of the matter distribution, galaxies are what are referred to as biased tracers, since they form only in very high-density regions – i.e. dark matter halos. So what we actually measure when we are trying to constrain cosmological parameter values is not the matter distribution at all, but rather the lensing and galaxy clustering signals.
Given a measured catalog of galaxies and a measured sky map of the lensing signal the quantities we actually measure are correlation functions (see also this bite) of these spatial distributions. At its core, a correlation function tells you how much more likely over random chance you are to find two objects separated by a fixed distance. In this case our objects are lensed photons (aka “cosmic shear”) and galaxies, but there is one more signal we can construct from our other two – this is the so-called “Galaxy-Galaxy Lensing” (GGL) signal. GGL is essentially a measure of cross-correlation between the matter and galaxy distributions, and is measurable when you have two populations of galaxies – a background population that acts as the source of gravitational lensing, and a foreground population that traces the matter responsible for the lensing signal.
So what do we do with all of these signals? In order to pump the maximum amount of information possible out of observational data, modern surveys such as DES employs a combined-probes analysis. A single observational probe can often only measure a combination of parameters of interest. Suppose probe 1 can only measure xy2, but probe 2 can measure xy. By dividing the measurement of probe 2 by probe 1, we can obtain y, which then allows us to find x. If we only had one probe, we wouldn’t be able to separate the parameters, and therefore could not know either. This is exactly the situation we solve (i.e. “breaking degeneracies”) by using measurements of the same parameter from multiple probes!
A complication to the degeneracy-breaking picture arises for combining galaxy clustering and lensing, however. On large scales, it really is as simple as the division described above, as the galaxy correlation function is simply a constant factor (termed the “bias” b) multiplied by the matter correlation function measured by lensing. But on small scales this relationship no longer holds – the bias now becomes “scale-dependent” (a piece of jargon that will be important for later!), and some complicated function is necessary to connect the galaxy correlation function to the matter correlation function. How do cosmologists deal with this complication?
Scale Cuts vs. Systematics
In an ideal world, cosmologists would be able to cook up a model that can describe the correlation function on any scale. Unfortunately, this is not possible in our universe due to the complicated physics of galaxy formation and impacting the inability of the correlation function to describe these small scales. There have been many attempts to parameterize the effect of galaxy formation on these small scales, but the choice of modern analyses (like that of DES) is to simply impose a scale cut – in other words, just ignoring the measurement of the correlation function below a certain scale. While this reduces the information that can be used to constrain cosmological parameters (resulting in a larger overall statistical error in the final result), the idea is that this cost is worth it in order to avoid modelling complicated galaxy physics.
In the last decade or so, several estimators have been proposed to try to incorporate scale cuts into the correlation function signal you actually measure on the sky. Today’s authors provide an update on an older estimator put forth to model cosmic shear, modifying it to instead describe galaxy clustering and GGL. In computing the correlation functions from a given set of cosmological parameters, one has to perform an integral. The estimator today’s authors use (the Ψ statistic) applies a weight to the integrand function that downplays the effect of small scales in the final correlation function. Figure 1 shows the impact of this estimator on the integrand function in the bottom panel as a function of multipole moment ℓ – which can be thought of as the inverse of the angular scale θ. The fact that the Ψ statistic is zero at very large and very low ℓ (very low and very high θ) means that the Ψ statistic is not sensitive to these scales. As further proof that this is true, the fact that the colored lines (representing two different models of scale dependent bias) are the same as the black line (constant scale-independent bias) in the lower panel for the Ψ statistic means that it is insensitive to the scale-dependent way galaxies trace dark matter. This is meaningful when compared to the usual galaxy clustering correlation function w(θ), which in the upper panel is clearly sensitive to all θ and changes noticeably between scale-dependent and scale-independent bias.
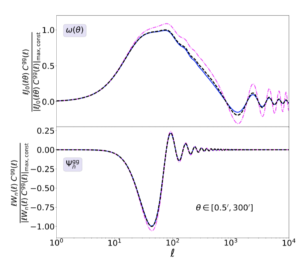
Figure 1: The function used to compute w(θ), the galaxy angular correlation function in the standard analysis (top) and the function used to compute the corresponding measure of galaxy clustering using the modified statistic Ψ (bottom). Here ℓ can be thought of as ~1/θ. Taken from Figure 5 of today’s paper.
So the authors have shown that using a new statistic (Ψ) in computing the correlation function means we do not have to think about scale dependence of tracers. How does this impact the final constraints on parameters we care about? Well, the authors show that not using Ψ, but rather using the standard correlation function analysis with scale cuts will produce a systematic error using the standard analysis. This systematic error is relatively small, but is reduced when Ψ is used – and the authors show in Figure 2 that there is essentially no downside in using Ψ, in terms of statistical error budget. Figure 2 shows parameter constraints quantified in terms of the matter overdensity parameter Ωm and the amplitude of the matter fluctuations σ8, both cosmological parameters that are constrained by the standard lensing and clustering analysis that the authors also try to constrain using Ψ. The size of the constraint contours for the standard analysis and the analysis using Ψ look almost exactly the same size – this means that by switching estimators the authors are hardly losing any information about the underlying cosmology.
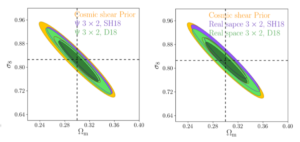
Figure 2: Constraint contours for the matter overdensity parameter Ωm and the amplitude of matter fluctuations σ8 – taken from Figure 11 of today’s paper. Though there is a slight offset in the contours between the modified (left) and standard (right) estimators, the areas and axis ratios are essentially the same. Here the SH18 and D18 contours correspond to two different choices of scale-dependent bias models, and the yellow contour represents the impact of cosmic shear, which the authors did not explicitly compute, so it is included as a prior.
Putting the “precision” in precision cosmology
Today’s paper shows that extremely careful consideration of your modelling process is necessary to unlock the full potential of your data. By changing the way they measure correlation functions, today’s authors showed they can reduce systematic errors in constrained cosmological parameters using the standard analysis. In the modern era of precision cosmology, any reduction in systematic errors improves a cosmologist’s understanding of their model – which makes other systematic offsets in constrained parameters, like the Hubble constant tension, all the more exciting!