Authors: Jens Stücker, Andreas. S. Schmidt, Simon D. M. White, Fabian Schmidt, Oliver Hahn
First Author’s Institution: Donostia International Physics Centre (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastian, Spain
Status: Submitted to MNRAS
Famously confusing to some, tides act to move part of an object relative to its center of mass. But, at least in the context of large-scale structure, we can explain that – sort of – and the authors of today’s paper can simulate it! Tidal fields, besides affecting our oceans, also play a role in the cosmic web. Tides can affect collapsing dark matter halos and the resulting galaxy formation inside them, so it is important to include them in our structure formation models!
You may have heard that on large scales (>100 Mpc), the universe is homogeneous and isotropic. However, on the scale of individual halos, gravitational tidal forces play a significant role in the dynamics by stretching and compressing matter. This deformation of matter picks out a preferred direction, introducing anisotropy. In ordinary N-body simulations, it is very challenging to separate out the effects of tidal fields from the full non-linear dynamics, as the tidal fields are constantly fluctuating. In particular, it is hard to know how much of the halo’s shape is due to the tidal field. The goal of today’s paper is to isolate the effect of the tidal field on halo shapes.
Stirring in some anisotropy
The authors of today’s paper isolate the effect of the tidal field by riffing on a technique called separate universe simulation. Separate universe simulations exploit the fact that a large-scale overdense region looks a lot like a universe with a higher value of ΩK, the curvature density parameter. We know today that in reality ΩK is very close to 0 (i.e. we live in a flat universe), but by changing the curvature in this way we can isolate the effect of large-scale overdensities in a way that is not possible in a flat universe.
The upshot of this is that you can run cosmological (N-body) simulations with a different cosmology (specifically a different curvature) to look in detail at the relationship between large-scale overdensities and smaller-scale ones. These earlier separate universe simulations were isotropic (i.e. symmetric under rotation), but today’s paper is the second in a series that takes this idea one step further by including anisotropy. The authors modify the simulation code GADGET to incorporate a large-scale tidal field in an analogous way to how changing the global curvature acts like a large-scale overdensity. They do this by changing the cosmological expansion from the isotropic expansion of our universe to one that has a preferred direction – in this case the z-direction.
Stretching and squashing
The tidal field in these simulations is parameterized in terms of the eigenvalues λ of the deformation tensor, which we need to unpack the meaning of. To think about the tidal field, it helps to think about the moment of inertia of a a ball of clay. The tidal field acts to deform our clay ball into a 3D object with three axes specified by the x, y, and z components of the moment of inertia. For the most symmetric of objects, i.e. a sphere, the moment of inertia components in the x,y, and z directions are all the same – this is essentially the case of an isotropic tidal field.
What today’s authors are doing is stretching our sphere into an (American!) football shape along the z-axis. Both the x and y components of the moment of inertia are going to be the same as for the sphere but the z-component of the moment of inertia will be larger than the sphere’s. How much larger is quantified by the eigenvalue in the z-direction (λz), which you can think of as the “stretch factor” – this is negative even though the moment of inertia z-component is larger, but this is just a mathematical convention. By stretching our sphere into a football, the authors have mimicked exactly the action the tidal field takes in the negative λz case! Similarly in the positive λz case, imagine squashing the sphere to produce a new pancake-like object. We can consider arbitrary combinations of squashing and stretching by the tidal field in this way for whatever funky 3D object you can come up with, which will in general have x, y, and z components in its moment of inertia.
The authors put a face on the tidal field right off the bat with some simulated halos (Fig. 1). Stretching or compressing (along the z-axis) occurs due to the large-scale tidal field, and clearly affects the overall dark matter halo shape. Here the “stretch factor” λz of 0.1 corresponds to a cosmological expansion that is about 10% faster in the z-direction than in the isotropic case. The previous paper in the series focused on large-scale forces, but here the authors have included smaller-scale forces between simulation particles as well, which have been modified to include the effect of the tidal field.
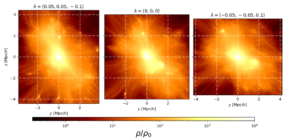
Figure 1: Here the same halo is shown in three different simulations with three different large-scale tidal fields. Left: A tidal field corresponding to a “stretch” in z Center: the case of no tidal field Right: a tidal field opposite to the “stretch” i.e. a “squash” in the z-direction. The colorbar shows overdensity (density divided by the mean) (Figure 1 from today’s paper)
Tidal (mis)alignments
The authors find that halos are sensitive to the external large-scale tidal field both in their inner and outer regions. One way they look at this is by comparing the moment of inertia tensor for halos to the tidal field. To do this they first define their halos using R200c, a proxy for the virial radius, and the corresponding virial mass proxy M200c (where (4π/3) M200c/R200c3 = 200 x ρcrit). Then, by considering many so-defined halos in their simulation, the authors find that the alignment of the halos with the large-scale tidal field is stronger for more massive halos. i.e. more massive halos are stretched more by the tidal field.
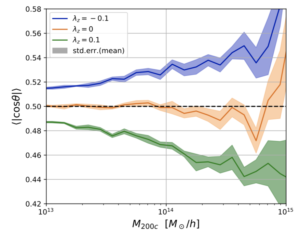
Figure 2: The impact of the tidal field on halo alignments. The value of the alignment between the tidal field and the halo as measured by |cosθ| (θ is measured between the z-axis and the halo axis with largest moment of inertia component) as a function of the virial mass proxy M200c. Here different tidal field configurations are shown for the stretched, squashed, and isotropic configurations with errorbars generated from simulations with different sets of initial conditions. The dashed line shows the expectation from random alignments. (Figure 5 from today’s paper)
The authors also quantify in more detail the misalignment between the halos and the tidal field. They measure the angle θ between the axis of the large-scale stretching/squashing due to the tidal field (the z-axis) and the halo major axis (as determined by the halo moment of inertia). This is shown in Fig. 2. They find that on average, for the isotropic case, the halo alignments are consistent with random alignments. However, for the stretched configuration, the long axis of the halos point more towards the stretching direction than in the case of random alignment. Similarly, for the squashed configuration, the long axis points farther away from the squashing axis, with respect to the case of random alignment. They emphasize that this shows a clear causal relation between large scale tidal field and galaxy alignment.
Why go to all this trouble?
Weak gravitational lensing observations are one of the primary drivers of large-scale structure constraints on cosmological parameters. However, weak lensing observables are sensitive to the tidal field, so tidal fields could be probed directly using lensing data, potentially giving better constraints on key quantities like the dark energy equation of state and matter density parameters. Beyond this, there is an important physical effect called intrinsic alignment in which galaxies are rotated by the tidal field toward or away from nearby large-scale structure. This is a story for another bite, but failing to include this effect in observations can lead to the wrong answer for the cosmological parameters we care about! For this reason, an isolated laboratory for testing out tidal fields like the simulations in today’s paper can be very helpful. Understanding non-linear physics is always going to be a little messy, but creative methods of simulation can help tide-y it up!