Title: H0 tension or T0 tension?
Authors: Mikhail M. Ivanov, Yacine Ali-Haı̈moud, and Julien Lesgourges
First Author’s Institution: Center for Cosmology and Particle Physics, Department of Physics, New York University, New York City, USA and Institute for Nuclear Research of the Russian Academy of Sciences, Moscow, Russia
Status: Submitted to arXiv [open access]
One of the most prominent issues in cosmology is the so-called “Hubble Tension”. It represents an unsolved issue in cosmology: Measurement of the Hubble constant H0, which tells us how fast the Universe is expanding, do not agree with each other. Observations of the cosmic microwave background (CMB) made by the Planck satellite suggest a value of 67.4 ± 0.5 km/s/Mpc, while observations of supernovae and cepheids by the SH0ES team suggest a higher value of 73.5 ± 1.4 km/s/Mpc (see this astrobite as well as this one for a description of H0 measurements with cepheids and supernovae). This tension between these measurements is a problem for the cosmological standard model In this model the two measurements should coincide. If they are not the same, the standard model might need to be adjusted. However, the authors of today’s paper discuss the possibility that the Hubble tension is actually caused by prior assumptions in the measurement analysis, in particular the assumed temperature of the CMB.
The mean temperature of the CMB – well-known but not measured by the Planck satellite
The Planck satellite measured the CMB anisotropies. These are the variations in the CMB radiation relative to the mean. Cosmological parameters, including the Hubble constant, influence the observed size and magnitudes of these variations. They can, therefore, be inferred from these anisotropies. To obtain the Hubble constant though, an additional parameter is needed – the mean temperature T0 of the CMB today.
The original fluctuations in the CMB are entirely independent of T0. Therefore no measurement of T0 was obtained by the Planck collaboration. In these cases, where the determination of a quantity depends on another parameter whose value cannot be directly determined, astronomers often use so-called “priors”. These are an assumed probability distribution of parameters, which incorporate our assumptions and pre-existing knowledge on them. Usually, the prior corresponds to the probability distribution of a parameter obtained by a different survey. With these, the “posterior”, which is the probability distribution of the desired parameters, can be estimated.
In the case of Planck, T0 was assumed to be T0 = (2.72548 ± 0.00057) K. This impressively precise measurement was obtained by a combination of balloon-borne and satellite probes like the FIRAS instrument on the COBE satellite. Using this T0, Planck could then estimate H0.
Exchanging priors and posteriors
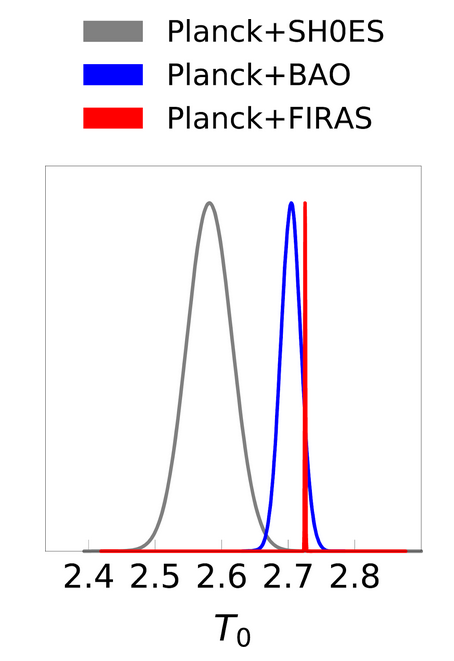
The authors of today’s paper turn this process around. They use H0 from SH0ES as the prior for Planck to obtain T0. The resulting probability distribution for T0 is shown as the grey curve in Fig 1., alongside the very tight constraint of FIRAS alone on T0. The T0 from the combined Planck and SH0ES measurements is in strong tension to the FIRAS measurement. So, instead of having very different values for H0 in Planck+FIRAS and SH0ES alone, we could have very different values of H0 in Planck+SH0ES and FIRAS alone. Consequently, there might not be a Hubble Tension, but instead a T0 Tension.
An independent referee: Baryon-Acoustic Oscillations
To decide between the different T0 measurements, the authors employed an independent referee: Baryon-Acoustic Oscillations (BAOs). BAOs are fluctuations in galaxy and matter densities that originate from density waves in the early universe. Due to these fluctuations, galaxies are denser at specific scales. From measuring these scales and the distance to the overdense galaxies, H0 can be estimated independently from the SH0ES and Planck measurements. The authors used the H0 from BAO observations with the BOSS survey, which they combined with the Planck data for an independent estimate of T0 (blue curve in Fig 1). This T0 is consistent with the FIRAS measurement and in tension with the result from Planck + SH0ES. Therefore, it seems, as if the FIRAS measurement is closer to the real value than the Planck + SH0ES T0.
Why not measure T0 directly?
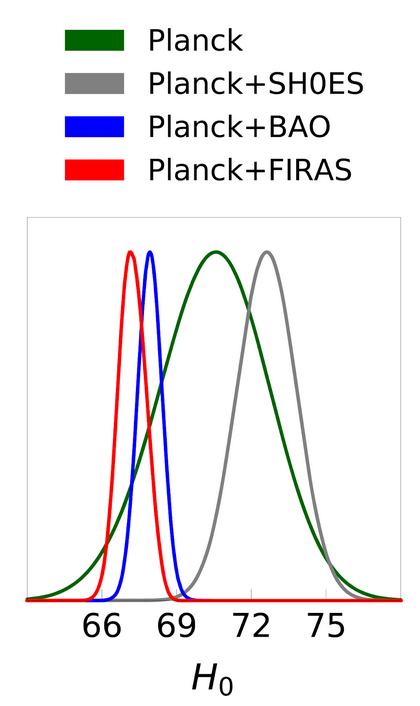
As mentioned before, it is not possible to measure the CMB temperature directly from the primordial anisotropies of the CMB. However, the authors show how to still infer T0 from just the Planck data. Their approach relies upon the fact that the CMB is distorted on its way to us. This distortion can be due to gravitational lensing or the integrated Sachs-Wolfe (iSW) effect. Lensing deflects and magnifies CMB photons, while the iSW effect causes CMB photons to lose a little energy when passing through gravitational potentials in an expanding universe. These effects depend on the temperature of the CMB and can, therefore, be used to constrain T0. From this measurement, H0 can then be determined without any external priors. The result for H0 is shown in Fig 2 as the green curve. However, the constraints on the T0 measurements are quite broad. Therefore, the H0 measured just from Planck data agrees both with the FIRAS and the SH0ES measurement. So while it is in principle a reasonable approach to use a prior-independent estimate of T0, it cannot really discriminate between the FIRAS and SH0ES values.
So, what do we learn from this analysis?
In conclusion, the authors showed that the Hubble tension can also be expressed as tension in CMB temperature T0. It could, therefore, be solved when a higher T0 is assumed as prior for estimating H0 from Planck data. However, this explanation seems unlikely, as BAO measurements support the lower T0 value. Nevertheless, the analysis showed that the solution to the Hubble tension might not be a change in the cosmological standard model, but rather a careful examination of the assumptions and priors that influence the measurement of H0.



Thank you for your article, but you used an outdated term: For the last couple of years, the “Hubble” constant has been named the “Hubble–Lemaître” constant, to bring terminology in line with the person, Georges Lemaître, who actually discovered it. For example, please see the following article on the same topic as yours: https://academic.oup.com/mnras/article-abstract/486/4/5046/5487522?redirectedFrom=fulltext
Hi, thank you for this comment! There is indeed some confusion regarding the correct term for H0. The International Astronomical Union (IAU) recommends using the term “Hubble Constant” when referring to H0. This is in line with the paper we discuss in this article. To honour Lemaîtres correct interpretation of H0 as expansion rate of the Universe and the creation of the Big Bang theory, the IAU has instead voted in 2018 to rename the “Hubble Law” (The redshift of galaxies in the local Universe is proportional to their distance) to the “Hubble-Lemaître-Law”. To learn more, you can have a look at the press release by the IAU regarding the name change of the “Hubble” law, and their background information here: https://www.iau.org/news/pressreleases/detail/iau1812/
I have one question regarding the SNe measurements. As was recently discovered, the 1a SNe have at least two origins: white dwarfs accreting matter and white dwarfs collision. The SNe resulting from white dwarf collisions cannot be used as standard candelas, however they cannot be distinguished from the accreting white dwarf. When a high-z SNe are searched, with increasing z rise the number of SNe caused by white dwarf collisions (because they are brighter, so easier to observe). If the dataset are not corrected to this rising number of SNe caused by white dwarf collisions, the measured H0 is shifted to higher values. Are the datasets corrected in this way?
The velocity distance Law should be more deserving-ly named the Hubble-Robertson law since Howard Robertson was the first to express the v = Hr relationship using Hubble and Humason ‘s data. Or better yet the “Friedmann-Hubble-Robertson-law” in order of the chronology. Just a thought