Authors: Adam G. Riess, Stefano Casertano, Wenlong Yuan, Lucas M. Macri, and Dan Scolnic
First Author’s Institution: Space Telescope Science Institute, Baltimore, USA and John Hopkins University, Baltimore, USA
Status: Published in ApJ [open access]
The “Hubble Trouble”
The Hubble constant H0 describes the rate at which the universe expands today. It is a fundamental parameter of the standard model of cosmology, the ΛCDM-model, which is well supported by a range of observations. However, in recent years there has been a controversy surrounding H0, called “Hubble Trouble” by popular media and “H0 Tension” by scientists. It comprises the discrepancy between measurements of the Hubble parameter by the Planck satellite (67.4 ± 0.5 km/s/Mpc ) and in the local universe (72.04 ± 2.67 km/s/Mpc). Up to now, this discrepancy was less than 3σ and could still be explained by a statistical fluke. In today’s paper, however, Adam Riess and his co-authors reduced the error bars on their measurement of H0 in the local universe and found that the discrepancy to the Planck measurement increases to what they call “beyond a plausible level of chance”. This could imply that the standard model is wrong and needs to be extended!
How to measure the Hubble Constant?
To understand how H0 was measured more precisely in today’s paper, let’s review how it is measured in the local universe in the first place. For this, “standard candles” are needed, which are sources with known luminosity. From this luminosity, the distance can be inferred by how bright they look — if they are fainter, they are farther away. With the distance D, the Hubble constant can then be calculated as H0=c⋅z/D, where c is the speed of light and z the redshift of the source, i.e. by how much the spectrum of the light source is shifted due to the expansion of the universe.
One popular kind of standard candles are a type of supernovae, the SN Ia. These supernovae all have the same intrinsic luminosity, so if they are at the same distance, they should all appear equally bright to us at their peak. So, from the peak apparent brightness, the distance to the supernova can be estimated. We can infer this peak apparent brightness from the light curve of the supernova, which is the time variation of its brightness . However, these light curves and therefore the distance relation must be calibrated with some SN Ia with known distances. And this is where Cepheids come in.
Cepheids are variable stars with a special relationship between their periods and their maximal luminosity, their so-called period-luminosity relation. Astronomers have measured this relationship very well with Cepheids in the Large Magellanic Cloud (LMC), and use it to measure the distance to Cepheids in the galaxies hosting the SN Ia calibrators. With these calibrators, the distance to other SN Ia is measured and H0 is calculated.
Nonetheless, there is one source of uncertainty in the observation of the Cepheids: While the Cepheids near SN Ia calibrators are observed by the Hubble Space Telescope (HST), the Cepheids in the LMC are usually observed with ground-based telescopes, as it is cheaper than observations from space. The ground-based observations use slightly different observational frequencies and are affected by the atmosphere. Therefore, these observations are not directly comparable to the HST measurements and introduce a 1.4 –1.8% error.
New Observations – Old Problem
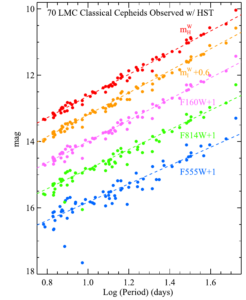
Figure 1: Measurements of the Period-Luminosity relations for the Cepheids in different wavelengths. The x-axis shows the logarithm of the cepheids’ period and the y-axis shows the apparent brightness in magnitudes, with lower values indicating a brighter star. Each color corresponds to different observed wavelengths. The dots are the measurements of the individual Cepheids, while the lines are the best-fit period-luminosity relations. Figure 3 in the paper.
To find H0 with higher precision, we need to get around this problem. Therefore, the authors of today’s paper use new observations of 70 Cepheids made directly with the HST. They measured the brightness of the Cepheids at different wavelengths, along with their periods to find a more precise period-luminosity relation. Figure 1 shows their measurements, along with the period-luminosity relations the scientists find for different wavelength bands.
With these new relations, the authors measure H0=74.03±1.42 km/s/Mpc (see Figure 2). This means that the results still do not match Planck’s low value. Even worse, because the error is reduced from 2.4% to 1.9%, the tension to Planck is increased to 4.4σ. Consequently, the H0 Tension is stronger!
This suggests that the standard model might not be the right description of the universe after all. Figure 2 mentions different possible new models which might explain the tension, among them additional dark energy in the early universe or new neutrino species. These additions could solve the tension and open the way to new physical models and theories!
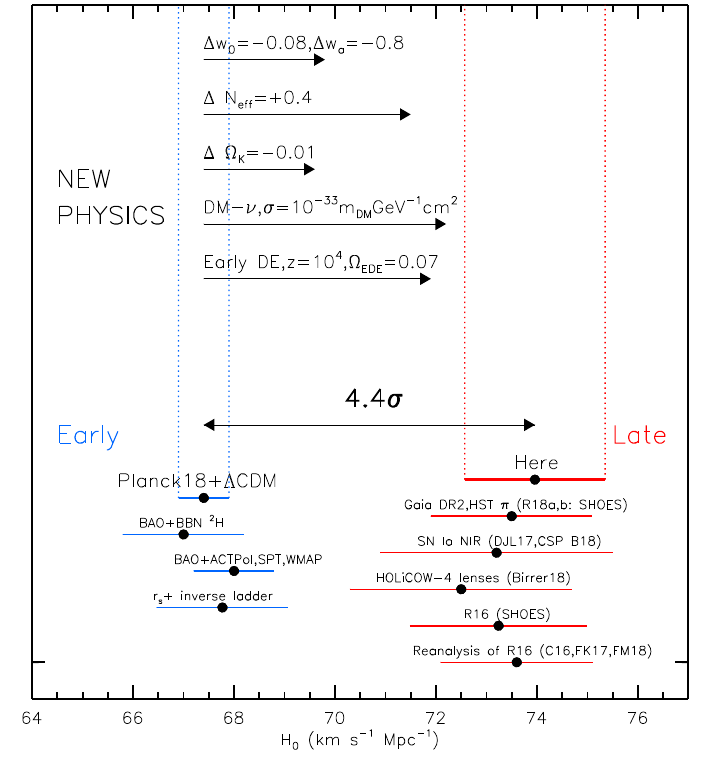
Figure 2: Different measurements of the Hubble constant in the early (blue) and local (red) universe. The measurements are significantly different from each other, which suggest that the current cosmological standard model is not correct. The new measurements (labelled “Here”) have the biggest tension to the early universe measurement. Above the measurements, the effect of different extensions to the standard model are shown. They are (top to bottom) a time-varying dark energy, additional neutrino species, a curved universe, interactions between dark and normal matter and additional dark energy in the early universe. Figure 4 in the paper.
What’s next?
The next step to study the H0 Tension is to continue measuring the Hubble constant with increased precision and see if the tension persists. The current uncertainty is caused mostly by the SN Ia calibrators, but future SN Ia observations will reduce it further. Also, more independent measurements of the Hubble constant are on their way, for example using strong gravitational lensing or the tip of the red giant branch. All in all, we seem to be on the brink of exciting new physics, so stay tuned for the next results on H0!



