Title: High accuracy on H0 constraints from gravitational wave lensing events
Authors: Paolo Cremonese & Vincenzo Salzano
First Author’s Institution: Institute of Physics, University of Szczecin, Wielkopolska 15, 70-451 Szczecin, Poland
Status: Open access on the arXiv
A Multi-Messenger Approach to a Cosmological Tension
The Hubble constant (H0) is an important cosmological parameter that governs the rate of expansion of our universe, and for which a value has not yet been universally agreed upon. This conundrum has been dubbed the “Hubble tension,” and has been covered in many previous astrobites articles (see here, here, here, here, and here). The Hubble tension boils down to how independent measurements of H0 can be made very precisely, but H0 values inferred from studying the “early” universe significantly disagree with H0 values inferred from studying the “late” universe. (What the phrases “early” universe and “late” universe mean is covered in more detail here.)
The statistically significant disagreement between H0 measurements has led to a call for further alternative and independent ways to measure H0, especially as we wait for more sensitive next-generation surveys (such as Euclid and the Square Kilometre Array, SKA) to become operational. The authors chose to study the possibility of constraining H0 by using gravitationally lensed observations of gravitational waves (GWs) and electromagnetic (EM) signals emitted by a single source. That was a dense sentence, so let’s take a step back!
Gravitational waves are ripples in space that result from accelerating objects; GW signals from the merger of compact objects (such as two neutron stars) are strong enough for observatories to detect. Our “ears were (first) opened” to the GW universe in 2015 with LIGO. Two years later, in 2017, the astrophysical community found EM counterparts to a GW detection, heralding a new era of multi-messenger astronomy, where astronomers can study a single source via its different types of radiation (“multiple messenger signals”). With GW and EM counterparts, a value of H0 can be derived independently from the aforementioned “early” universe and “late” universe measurements. In fact, such a measurement has already been done (covered in this astrobite!), although it is worth noting that this measurement, despite being consistent with other measured values, doesn’t add much information to the Hubble tension debate because of its large error bar.
A Lensed Look into the Universe
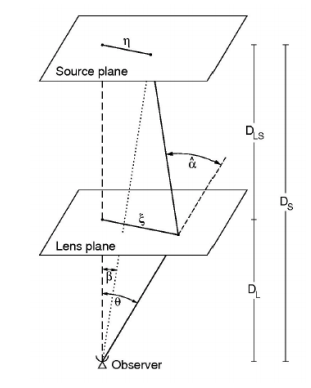
Nonetheless, GW and EM counterpart signals might still provide useful constraints on H0 if they are gravitationally lensed. In a gravitationally lensed system, signals from a background source follow different paths around a foreground lensing source. Figure 1 shows us what a gravitational lens system looks like. The time delays between these signals depend on whether the radiation is in the EM or GW regime; the difference between the time delays is called the “arrival time difference.” Typically, the gravitational lensing of EM signals can be studied geometrically, but for low frequency lensed GW signals where the mass of the lens is small enough, wave optics approximations must be made. (As a side note, there was recently speculation about whether a gravitationally lensed GW signal had been detected, covered in this astrobite. Spoiler alert: it was likely just a “spooky cosmological coincidence.”)
The authors show that the arrival time difference between lensed GW and EM signals also depends on cosmological parameters such as H0. In order to investigate how precisely this difference can constrain H0 values, they calculate the arrival time difference for a large set of input cosmological parameters—the matter density parameter, H0, and the dark energy equation of state parameter—and two different mass models for the gravitational lens. Both a “pessimistic” (present-day) scenario and an “optimistic” (future-day, like with SKA) scenario for the rate of GW detection by pulsar timing array observatories were considered. These two different scenarios were important for determining uncertainties on the calculated arrival time difference—the smaller the uncertainties, the more sensitive arrival time difference observations would be to H0 values.
When assuming a standard ΛCDM cosmological model, the authors find that even one single lensing event in the “pessimistic” scenario would provide fundamental information about H0 with errors comparable to other H0 measurements available today. For the “optimistic” scenario, the uncertainty on H0 would be better (smaller) than present-day measurements by two orders of magnitude. Relaxing cosmological background assumptions, such as models where the dark energy equation of state parameter is not -1, greatly increases the uncertainty on H0 measurements. A higher number of observations would be necessary to reduce the uncertainty, which would be difficult considering the low probability of lensing event detections. Still, the results are exciting—multi-messenger gravitational wave signals can, in the near future, provide a measurement of H0 with uncertainties comparable to present-day measurements.