- Title: Towards Realistic Progenitors of Core-Collapse Supernovae
- Author: W. David Arnett, Casey Meakin
- First Author’s Institution: Steward Observatory, University of Arizona
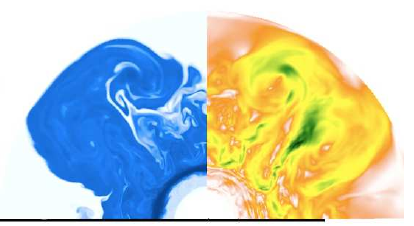
An "eruption" of turbulent instabilities occurring about 11 minutes into the simulation of a core-collapse supernova. The blue side depicts the mass fraction of Si (showing where nucleosynthesis products have spread) and the right side depicts the velocity of material. From Figure 4 of Arnett & Meakin 2011.
I promised to write more about supernovae after I posted my brief introduction to these explosions and the influence they have on the universe, so I couldn’t pass up this new work by David Arnett, who has been a major figure in supernova research since the mid-1960s, and postdoc Casey Meakin.
The basic model of a core collapse supernova goes as follows. Stars more than about eight times the mass of our sun live very short lives (less than about 50 million years) as main sequence stars that burn hydrogen in their core. Once these massive stars have fused most of the hydrogen in their cores to helium, they leave the main sequence and move on to burning helium in their core…. and then they burn carbon… and then oxygen, and so on until, finally, they are left with an iron core. This evolution leaves behind a mantle of H, He, C, etc. shells in an “onion skin” structure. Once an iron core is achieved, the process ends because Fe is at the peak of the curve of binding energy and fusing Fe into heavier elements will not yield more energy. Chaos then breaks loose in the star as it has lost its source of supporting pressure, and the resulting explosion (a “core-collapse” supernova) releases about ergs (
J) of energy.
This basic sketch only begins to describe the complexity of the later stages of the star’s evolution and the explosion physics. Chapter 15 of Carroll and Ostlie’s ubiquitous textbook, “An Introduction to Modern Astrophysics” is filled with more details, but core-collapse supernovae are not yet perfectly understood.
Arnett and Meakin’s latest work improves our understanding of core-collapse supernovae by simulating the evolution of a progenitor star near core-collapse hydrodynamically in two-dimensions. In this way they can study the mixing that occurs between the shells in detail. This mixing is the result of a number of advection (large-scale flow) and diffusion (random, small-scale motions) processes due to, for example, pulsating bursts of energy injected by nuclear burning.
The simulation starts with the initial conditions of C, Ne, O, and Si burning shells as predicted by another simulation (obtained by them via private communication; i.e. not yet published) for an evolved 23-solar-mass star a mere hour away from core-collapse. These chosen initial conditions are one-dimensional (i.e. spherically symmetric), but turbulent instabilities begin to develop about 6 minutes into the simulation. The simulation calculates the evolving temperature, pressure, velocity, chemical composition, etc. of each point in the model in response to these processes.
Because computational power is limited, the quality of a simulation in reproducing observed phenomenon depends on the accuracy of the approximations that are made to the fundamental laws of physics acting on particles below the resolution of the simulation. The authors argue that the turbulent mixing exhibited in the figure above clearly demonstrates why a 1D (spherically symmetric) model would be insufficient to describe the structure of the supernova progenitor. The instabilities present in the progenitor are expected to have significant effects on the explosion physics as well as the properties of the remnant star – many researchers are studying the “kick” velocity expected for neutron stars born from supernovae.
The authors argue that a three-dimensional simulation necessary to truly model the physics of the explosion is within the reach of current computational facilities. To illustrate the need for 3D simulations, they discuss past simulations in 1, 2, and 3 dimensions that produced qualitatively different hydrodynamic results (convection topologies). This is primarily due to the effect that artificially constraining motion to a lesser dimensionality has on the conservation of angular momentum in the system. For example, cyclones are produced in a 2D simulation that would not be stable in 3D. They discuss a number of other frontiers for improvement as well, such as allowing for contraction of the iron core. For all the progress that Arnett and (many) others have made in simulating supernovae in the past several decades, there is plenty more work to be done.



Trackbacks/Pingbacks