Title: The Milky Way has no thick disk
Author: Jo Bovy, Hans Walter-Rix, David Hogg
Lead Author’s Institution: Institute for Advanced Study
It is written in The Standard Lore of Astronomy – a leather-bound book professors keep under their desks – that stars in the disks of spiral galaxies have a bimodal distribution of scale heights. Let’s back up a bit and explain exactly what I mean by that. To a decent level of approximation, most of the stars in disk galaxies are contained within a 2D sheet of stars. The stars orbit within a plane defined by the angular momentum vector of the galaxy. However, that’s not the whole story. Disk stars also have a component of their orbits in the vertical direction. Taken as a whole, the population of disk stars exhibit a distribution of vertical heights, characterized by a scale height, h. For a population of disk stars with a single scale height, the probability of finding a star at a given height z above the disk is proportional to exp(-z/h). Thus, the statement I made earlier, that stars in disk galaxies are characterized by a bimodal distribution of scale heights, implies that disk galaxies are really composed of two different kinds of disks: a thick disk and a thin disk. Disk stars at large heights (and thus likely members of the thick disk) are generally observed to be old and metal-poor. Stars in the thin disk, like the sun, are generally younger and have a metallicity comparable to the sun. Today we will be discussing a paper that comes to the conclusion that the notion of a thick disk and a thin disk is actually a poor approximation to the true distribution of disk stars. The authors of this paper propose that stars in the disk have a smooth and featureless distribution of scale heights.
This conclusion is based on data from the G-dwarf sample in the SEGUE survey. SEGUE – the Sloan Extension for Galactic Understanding and Exploration – uses the Sloan telescope (of SDSS fame) to obtain spectra of stars in the disk and halo of the Milky Way. From these spectra, one can infer the spectral type, iron metallicity, and abundances of other common elements. In particular, it is very instructive to look at the iron metallicity relative to the sun, [Fe/H], and the α-element abundance relative to iron [α/Fe]. Alpha elements like C, N, O, and Ca, are produced in triple-alpha reactions in the cores of red giant stars. The iron abundance gives an observer information about the age of the star, since older stars were born in an epoch when a large fraction of the heavy elements in the universe had yet to be synthesized. The α element abundance hints at the star formation history of a stellar population, since α elements are produced in large quantities relative to iron by core-collapse Type-II supernovae, which only occur in young stellar populations, but are produced at much lower levels relative to iron in Type-Ia supernovae, which do not occur until a stellar population is old enough for a significant population of white dwarfs to emerge.
In a previous work, Jo Bovy and collaborators binned stars in ([Fe/H],[α/H]) space and found that stars within each bin are well characterized by a single scale height. This observation is interesting, since presumably all of the stars that formed with a particular abundance pattern did so at roughly the same period in galactic history. This is also a very useful observation, since it allows one to infer how much stellar mass is in stars with a particular scale height. In principle one knows from stellar population synthesis models how much total stellar mass is associated with a number count of G type dwarfs and one can correct for the selection bias and limited volume of the SEGUE survey, which probably missed many G dwarfs in the survey volume. Of course, the devil is in the details, and modeling uncertainties imply that any error in the completeness correction and stellar population synthesis modeling could significantly change the authors’ results.

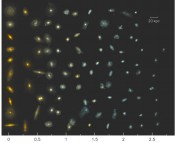
The distribution of stellar mass in the disk of the Milky Way (here plotted in terms of stellar mass surface density) as a function of vertical scale height. The average of the sample is plotted as a black line, and individual data points from mono-abundance stellar populations are plotted as circles colored according to the abundance of α elements.
Ignoring that caveat, the final result is striking. The authors calculate the surface density of stars in the disk of the milky way at the solar circle Σ(R0), as a function of scale height, h. This result is plotted as a black solid line above. The individual data points are the average mass surface densities and scale heights for each subsample in ([Fe/H],[α,Fe]) space and are colored by the α-abundance relative to iron. Stars that are α-enhanced tend to have large scale heights, while stars with α-abundance consistent with solar ([α,Fe] ~ 0) tend to have relatively small scale heights. If one looks only at α-abundance, there do appear to be two populations. However, closer inspection, and weighting stellar counts to infer the stellar mass distribution, reveals that stars have a smooth distribution of scale heights. Most of the mass is in stars small scale heights, traditionally associated with the thin disk. A smaller portion of the mass is in stars with large scale heights, traditionally associated with the thick disk. However, there is also a population of stars with intermediate scale heights, with no clear break in the mass distribution at any scale. Thus, assuming the modeling uncertainties have been correctly accounted for, there is no thick or thin disk, only a single, more complicated disk composed of stars with a range of scale heights.