Title: “Galaxy,” defined
Authors: Beth Willman & Jay Strader
First Author’s Institution: Haverford College
Words about Words
“The classification of astronomical objects is more than a semantic pursuit. Words matter. The terminology we choose to describe our research affects how appealing and accessible it sounds to funding agencies and the public. Words also dramatically affect the research community’s ability to draw global conclusions from diverse sets of astronomical objects.”
Astrobites is about communication, and about words. We aim to dissect jargon and parse technical details in order to report the essence of a scientific result. It is unusual to see a journal paper that so cogently states the importance of clear communication in science, one that specifically draws attention to the words we use. Willman and Strader, the authors of the paper discussed in today’s Astrobite (from which the above quote was taken), investigate a fundamental question that is all about words: just what, exactly, is a galaxy? How does one define such a class of objects? I clearly remember asking one of my undergraduate professors “What is the official scientific definition of a galaxy?” and then being overwhelmed by the long list of explanations, conditions, and caveats. My conclusion was that it was impossible to come up with a single definition: “you’ll know one when you see one” appeared to be the only answer, and that seemed neither scientific nor satisfactory to me. There is such a range of galaxy properties – spiral vs. elliptical, bulge-dominated vs. disk-dominated, interacting vs. isolated, bright vs. dim, large vs. small, the list goes on. Is there in fact a single, underlying thing that separates this diverse zoo of objects from others such as star clusters? The authors provide strong evidence to say: “yes, indeed.”
Galaxy, Redefined
Previous attempts at defining a galaxy have often appealed to size, dynamics, and/or complexity of stellar populations. However, it is becoming clear that there is no single dividing line in any of these categorizations; for example, there are objects classified as globular clusters (GCs) that are larger (in terms of mass in stars) than some very small dwarf “galaxies.” A more common recent definition appeals to the presence of dark matter: a galaxy contains it, while a star cluster such as a GC does not. However, this method of classification is based on a theory, not a physical law, and thus lacks generality. To address the shortcomings of these ideas, the authors boldly propose the following physically motivated definition:
“A galaxy is a gravitationally bound collection of stars whose properties cannot be explained by a combination of baryons and Newton’s laws of gravity.”
This formulation avoids a direct dependence on any particular model – including relying explicitly on cold dark matter (CDM). Of course, it is also fully compatible with a CDM model, in which case the definition simplifies to “A collection of stars that includes dark matter,” but its generality is both aesthetically and practically appealing. In the remainder of the paper, Willman & Strader examine two diagnostics that can be used to help classify borderline objects, then examine several classes of such objects, including those previously classified as dwarf galaxies and globular clusters
Am I a Galaxy, Doc? What’s the Diagnosis?
The most straightforward way to test if an object is consistent with Newton’s laws of gravity is to conduct a kinematic study, i.e. to analyze the motions of the constituent stars (and gas) that make up the system. Assuming that the system is in dynamical equilibrium – that the magnitude of the total potential energy is equal to twice the kinetic energy – a so-called “dynamical mass” can be derived*. Let’s do this to order of magnitude: the total kinetic energy (KE) of a system of total mass M is just ½M<v2>, while the potential energy (PE) is GM2/r by Newton’s law of gravity (G is the gravitational constant). For a spherical system in which objects have random orbits, the velocity dispersion (the standard deviation of the distribution of velocities in the system) describes the stellar motions very well, so use this for <v2>. Then, given the size of the system r, solve 2 KE = PE to get Mdynamical ~ rv2/G. This dynamical mass can then be compared to the total mass present in stars, gas, and stellar remnants (i.e. the total “baryonic mass,” or observable mass). The baryonic mass can be estimated in a number of ways: if the system is fairly nearby, the individual luminosities of the brightest stars can be measured, and then converted into stellar mass using an assumed distance, stellar population model, age, and stellar mass-to-light ratio. The gas content can generally be directly observed, typically in the radio; estimating the mass in stellar remnants requires more complicated modeling, but can be inferred using the same age and stellar population models used to determine stellar mass. Then if the total baryonic mass is significantly less than the dynamical mass, Newton’s laws are not happy with just the baryons, the definition is satisfied, and the system is a galaxy!
But not so fast. The above calculation is subject to several caveats, some of which are discussed by the authors of this paper. For example, some of the stars whose velocities are measured might not actually be bound to the system, and their higher velocities would cause the dynamical mass to be overestimated. Or, if the system contains few, dim stars, the measurement uncertainties might be such that both galaxy and star cluster interpretations are tractable. Stellar masses could also be underestimated if there were a large number of compact objects, such as white dwarfs or neutron stars, which went undetected. Perhaps another diagnostic of a system’s mass and size – of its potential well – is needed.
Wishing in the Potential Well
Willman & Strader suggest what might at first glance seem to be a very unusual way to probe a system’s potential well: the spread in metallicity (specifically, in the ratio of iron to hydrogen, [Fe/H]) amongst the stars in that system. As discussed by Nathan in this excellent Astrobite, the size of a galaxy’s potential well determines what fraction of material ejected by supernovae the galaxy is able to retain. Iron is produced in both Type Ia and Type II supernovae; if a system is unable to retain any of that iron, each generation of stars will have about the same metallicity and there will be almost no spread in [Fe/H]. Conversely, a large spread in [Fe/H] implies that successive generations of stars were more and more enriched, and thus that the system was able to retain some fraction of the material in supernovae ejecta.
The authors use publicly available [Fe/H] measurements and a Bayesian Markov Chain Monte Carlo algorithm (see this guest Astrobite for a great introduction to Bayesian analysis) to fit metallicity distributions to 40 systems (16 dwarfs and 24 GCs, by previous classification) to derive σ[Fe/H], the spread in metallicity for each system. They plot σ[Fe/H] vs. the absolute magnitude MV of the system in Figure 1, which is the main scientific result of the paper. Remember that magnitudes decrease for brighter objects, so the plot shows dimmer systems on the left and brighter systems on the right. The globular clusters and dwarf galaxies form two clearly separate populations in the figure. The former, in red, all (but two) lie at the very bottom of the plot: these systems did NOT retain much iron at all! The latter, on the other hand, show significant [Fe/H] spreads, indicating that they were able to retain supernova ejecta. The authors conclude from this analysis that σ[Fe/H] > 0.2 and MV > -10 indicates a galaxy classification by their new definition. Interestingly, the two GCs that lie above the trend, M54 and ωCen, have been previously suggested to be the disrupted cores of dwarf galaxies, and this diagnostic provides additional evidence that this may have indeed been the case (although there are a number of other considerations; see the paper for full details).
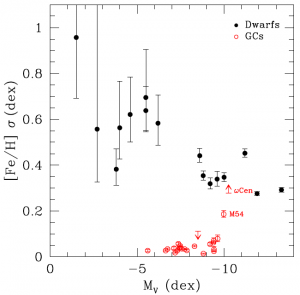
Figure 1: Spread in metallicity vs. brightness (which increases towards the right) for previously identified globular clusters (red) and dwarf galaxies (black). Metallicity spread σ indicates enrichment of successive stellar generations, and thus a deeper potential well that requires more than baryons and Newtonian gravity to explain. The authors propose that systems with M_V > -10 and σ > 0.2 should be classified as galaxies.
The authors go on to consider several classes of objects in detail, including “ultra-faint dwarfs” (UFDs; those fainter than MV~8), ultracompact dwarfs (UCDs; -13 < MV < -9 and sizes between 10-100 pc), “tidal dwarfs” (objects formed in the tidal interaction of two larger galaxies), and GCs. Broadly, they find that GCs as a population fail both of the above diagnostics for galaxy classification, and that UCDs cannot be unambiguously classified with kinematics alone. However, the few UFDs with reliable kinematics and metallicities are consistent with their definition of galaxy. They also point out that there are many candidate UFDs that, if confirmed to be galaxies, would increase the number of known galaxies at the low-luminosity end of the distribution by a huge factor. This could have profound implications for galaxy formation and cosmology.
What’s Next?
Having proposed and vetted a new definition of a galaxy, the authors conclude with a laundry list of suggested observations, which includes challenging but feasible measurements such as metallicity determinations of GCs in M31, studies of [Fe/H] spreads in faint UCDs and large GCs to probe systems near MV~10, and further observations of UFDs to probe galaxy formation in the low-luminosity regime. But will the new definition stick? Only time will tell. Perhaps the next generation of astronomy students will get a satisfactory answer when they ask their professors “What is a galaxy?”
*This type of analysis of bound systems, which is also referred to “virial” analysis, is extremely common in all areas of astronomy, and relies fundamentally on the simple form of the virial theorem; see this excellent web page for more.





One of the most clear, simple and well-written astrobites…