For many physicists, the fireworks on this fourth of July felt not like a testament to the birth of the United States of America, but rather to the birth of a new particle. That morning, the European Organization for Nuclear Research (CERN) verified the tantalizing rumors by announcing the discovery of the elusive, long-sought Higgs boson at a 99.9999 percent confidence level. If that’s not worthy of a fireworks display, I’m not sure what is.
The previously theoretical Higgs boson is an elementary particle that plays a crucial role in endowing particles with mass. It is a quantum — a particle manifestation — of the Higgs field, a field that permeates the entire universe. Every massive particle couples to this field to some degree, and it is this coupling that gives the particle mass. In a universe without mass, particles would bounce around aimlessly at light speed — there would be no galaxies, no planets, and no human beings.
This particle is truly fundamental to the universe as we know it. It’s the last of the major particles to be detected in the Standard Model: the unified theory that describes all known subatomic particles and the forces that mediate their interactions.
While fundamental to matter, the Higgs boson has remained undetected for so long for good reason. Once it forms through particle collisions in the Large Hadron Collider (LHC) it only exists for a billionth of a billionth of a billionth of a second before rapidly decaying through a series of unstable particles. So how do we know it was ever there in the first place? Particle physicists record the end results in order to reconstruct the entire particle cascade.
This may seem like a daunting task, but it can be done. Particle physicists first calculate the expected background, or the total signal from decays due to currently known particles. If there is an excess signal above this background, at a specific energy, this indicates a new particle that wasn’t included in the expected calculations (and thanks to Einstein, this energy also indicates the mass of the particle).
In order to detect the Higgs boson signal above the noise, we collide particles countless times and build up the signal from the decay. Particle physicists require that this extra signal be “five-sigma” above the expected background to count as a new particle.
Previous Results
Now you may be thinking: sigma what? A “sigma” — technically a standard deviation (but it’s usually represented by the greek letter sigma) — is a measurement of how unlikely a result is based on what you have assumed. Say we want to know if a coin is fair, with equal probability of flipping heads or tails. Flipping it twice and getting tails both times doesn’t mean the coin is weighted — it’s random noise. We’re within one-sigma of fair. But flipping the same coin 100 times and getting tails every time would be a signal many sigma away from fair — your assumption that the coin was fair has been disproved, and you have detected that the coin is weighted.
Particle physics follows certain statistical laws. The decay path the Higgs boson (as well as any other particle) follows is known within a certain margin of error. We have to account for this error in order to evaluate our results correctly. The background we observe from particle decays follows certain probabilities, but they’re still random decays. To find the Higgs, we “assume” that it isn’t there, and calculate what we expect to see. Then we look for a deviation from what we expected strong enough to disprove our initial assumption.
After just one or two collisions, we might see a spike above our expected background, but that doesn’t mean we’ve seen the Higgs — it could just be noise, like the coin that flipped tails twice. But the more times you flip the coin, the closer to 50 percent you should flip heads, and the lower the statistical fluctuations.
The rule of thumb in physics is that one-sigma means the result could be due to random fluctuations, while three-sigma counts as an observation. In order to claim a discovery, however, particle physicists require a five-sigma result, or a confidence level of 99.9999 percent. At this level, the chance that the result is erroneous due to random statistical fluctuations is only one in a million. Those are pretty good odds.
Last December, CERN announced a few preliminary results (see a previous astrobite). The ATLAS experiment detected a slight excess above the expected background energy at 126 GeV. The significance of this result was 2.5-sigma, or a confidence level of 98 percent. The CMS experiment noted an excess energy at 127 GeV. This significance was smaller at 1.9-sigma, or a confidence level of 94 percent. The results from December were promising, but with such low confidence levels were not final. A definitive answer required more data … data that we finally have.
Without Further Ado … The Higgs boson!
As of the fourth of July, both the ATLAS and CMS detectors found a signal between 125 and 126 GeV at the five-sigma level. In other words they claim this discovery with a 99.9999 percent confidence level. It’s even more promising because both experiments found the signal independent of each other.
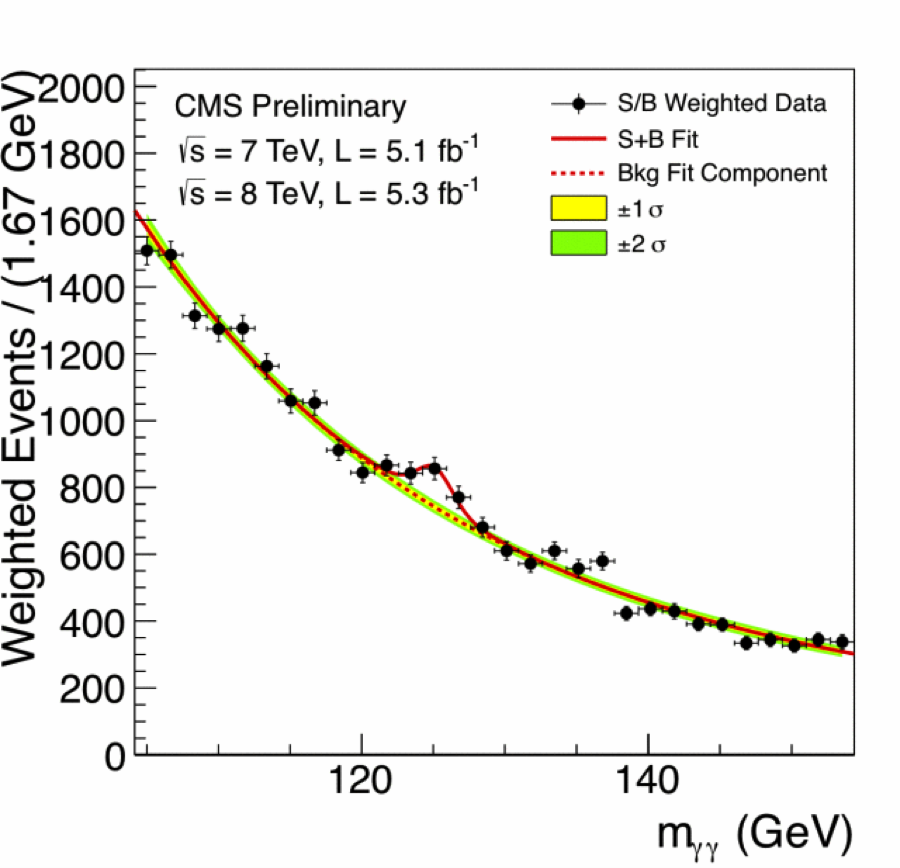
Figure 1 – Results from the CMS experiment. The slight excess energy at 125 GeV is seen at the five-sigma level. Photo credit: http://cdsweb.cern.ch/record/1459463
This excess energy is certainly the discovery of a new particle. And the energy it is located at matches our predictions for the Higgs boson. This $10 billion effort involving 6,000 researchers and a 26 km underground tunnel has finally seen the footprint of the Higgs boson. It is an incredible triumph where experiment proves theory true, and is the first step in truly understanding the concept of mass in the universe. It is but one example of the potential we have to understand the vast complexities of the universe driven by pure curiosity.



Trackbacks/Pingbacks