• Title: Sizes of Protoplanetary Discs after Star-Disc Encounters
• Authors: Andreas Breslau, Manuel Steinhausen, Kirsten Vincke, Susanne Pfalzner
• First Author’s Institution: Max Planck Institute for Radio Astronomy
• Status: Accepted for Publication in Astronomy & Astrophysics

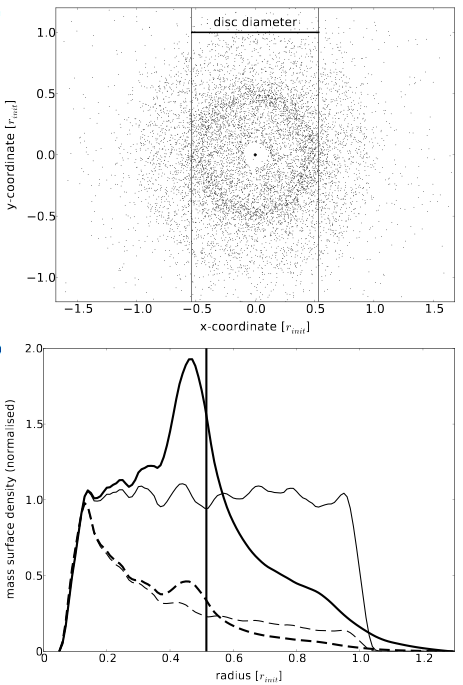
Fig 1: (Top) Face-on view of a simulated disk after an encounter with a mass ratio of 1 and a periastron distance of 2 r_init. The vertical lines show the measured size of the disk. (Bottom) Initial (thin) and final (thick) particle density (solid lines) and mass density (dashed lines) of the disk. The vertical line shows the point of steepest mass density decrease.  (From Breslau et al. 2014)

Close Encounters of the Stellar Kind

Stars often form in clusters, where the chances of a close encounter with another star are high. “Close encounter” just means that the passing star comes close enough that its gravity significantly affects the motion of the other star. The distance between the two stars at their closest point during the encounter is called the periastron distance, and these “close” encounters can occur at periastron distances of tens or even hundreds of AU.

The protoplanetary disk of gas and dust that surrounds a young star can be affected by the gravity of the passing star and will often end up smaller than it was before the encounter. For example, the density of material in our own Solar System drops off greatly past about 30 AU. Since the Sun formed in a cluster, this truncation might have been caused by a stellar encounter after the Sun’s disk had formed but before the cluster dispersed. According to previous models, the other star needed to come within about 100 AU to truncate the Sun’s disk at 30 AU.

This disk truncation scenario has been studied by various theorists in the past, who modeled what happens to a disk during an encounter between equal-mass stars and found that disks are typically truncated to about 1/2-1/3 the periastron distance. The authors of this paper wanted to explore a much larger parameter space and determine what relationship the final disk size has to the mass ratio of the two stars and the periastron distance.

Simulations and Results

The authors ran over 100 N-body simulations of a disk of particles experiencing an encounter with another star. Each simulation had a different stellar mass ratio and periastron distance. The authors restricted their parameters to ensure their systems were realistic. For example, they chose from a range of mass ratios based on values estimated by observing young dense clusters in our solar neighborhood. They also chose periastron distances that were small enough that the disks were perturbed but not so close that the disks were destroyed, because unaffected or completely absent disks wouldn’t be very helpful to their investigation.

Disk edges are fuzzy and don’t have clear cutoffs, so the authors had to define what they meant by ‘disk size’ before they could measure it. For this paper, they defined the disk radius as the distance from the star at which they measured the steepest drop in mass surface density (see Fig 1). You can see the resulting measurements of final disk size vs. periastron distance for several different mass ratios and different initial disk sizes in Fig 2.

From their simulation results, the authors derived the following simple relationship between final disk size (r_disk), stellar mass ratio (m₁₂), and periastron distance (r_peri):

r_disk = 0.28 m₁₂^-0.32 r_peri.

Notice that according to these results, the finial disk radius does not depend on initial disk radius! The only caveat is that the disks in these simulations never grow in size. For example, the equation above might predict that the final disk size should be 150 AU, but if the initial disk size was 100 AU, it will still be 100 AU at the end of the simulation.

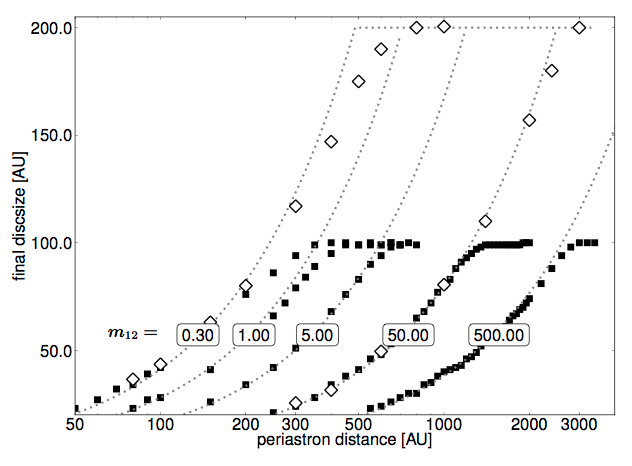
Fig 2: Final disk radius vs. periastron distance for simulated disks with initial radii of 100 AU (black squares) and 200 AU (white diamonds) for different mass ratios. (From Breslau et al. 2014)

What Does It All Mean?

Disks are truncated through gravitational perturbations in two ways. Some dust is removed by the passing star, but other dust  simply moves inwards as its angular momentum is transferred to the passing star. The authors show that this second effect is more significant than mass removal in truncating disks by noting that some of their simulated disks got smaller with no loss of mass. They also compared their results with the commonly-used approximations from previous equal-mass star studies and found that these approximations tend to overestimate the size of the truncated disk. However, the authors did confirm previous results that a disk like the Solar System could be truncated to 30 AU with a 100 AU periastron encounter with an equal-mass star, supporting the theory that the Solar System may have been affected by a stellar encounter. They also show that a larger or smaller mass star could be the culprit depending on its periastron distance.

The new ALMA observatory will let us measure disk sizes to much greater accuracy and allow us to study their dependence on mass ratio and periastron distance. This paper will prove very helpful in understanding those results and the encounter history of observed disks.

• About the Author

About Erika Nesvold

I'm a graduate student in the Physics Department at the University of Maryland, Baltimore County. I do my research at NASA/Goddard Space Flight Center with Marc Kuchner. I'm writing a model of debris disks to understand the way disks and planets interact, which will help us find exoplanets using images of disks. My model includes collisions, so I spend a lot of my day thinking about asteroids smashing into each other.

Related posts:

Stellar Flybys and Damping Disks: How to Excite an Exoplanet Stealing from the Solar System: the Effects of a Stellar Fly-By Mercury’s surprising density: What about magnets? Wreaking Havoc with a Stellar Fly-By