- Title: An Independent Method for Determining the Age of the Universe
- Authors: D.E. Winget, C.J. Hansen, J. Liebert, H.M Van Horn, G. Fontaine, R.E. Nather, S.O. Kepler, & D.Q. Lamb
- First Author’s Institution: The University of Texas at Austin
The Debate over the Age of the Universe
The first observational evidence that the universe had a finite age came through Edwin Hubble’s observations of galaxy redshifts in 1929, along with the theoretical framework produced by George Lemaitre two years before. For the next seventy years, there raged a debate as astronomers continually tried to nail down the exact age using a couple of main methods. Allan Sandage and Martin Schwarzschild measured the age through the study of globular clusters. As the most massive stars evolve the fastest, they studied this Main Sequence turn-off to determine the age of the cluster and thus infer the age of the universe. This method tended to give an age of the universe around 18 Gyr. Various measurements of Hubble’s Constant also supplied ages because the inverse of the Hubble Constant gives an age. Allan Sandage and Gerard de Vaucouleurs were the primary debaters over this value, arguing for 50 km/s/Mpc and 100 km/s/Mpc, respectively. These two values correspond to an age range between 10 and 20 Gyr.
In today’s Astrophysical Classic, we hark back to 1987 and the introduction of a new method of cosmochronology (dating the universe) through the use of white dwarf stars.
A New Approach
97 percent of stars become white dwarfs, all the stars with an initial mass less than eight solar masses. When white dwarfs form as part of a planetary nebula, they are very hot. As they are no longer undergoing fusion in their cores, they radiate heat away and slowly cool off. The authors realized that you could use the temperature of white dwarf stars to measure primarily the age of the Galactic disk, and secondarily the age of the universe.
Consider a star that was formed on the main sequence at the earliest possible time and became a white dwarf. This white dwarf star would now have a temperature that sets a lower limit on the temperature of all possible white dwarf stars because it has been cooling off the longest. If you look at the temperature distribution of white dwarf stars, there should be a cut-off at this low temperature. From this, with some assumptions we will go through momentarily, you can extract the age of the universe.
The Known White Dwarfs
Figure 1 shows the observed white dwarf luminosity distribution. The authors took the known white dwarfs and determined luminosity from the measured temperature. Using distances determined from proper motion measurements, they were able to determine the luminosity distribution: the number of white dwarfs per cubic parsec per bolometric magnitude. Recall that the bolometric magnitude is the magnitude accounting for all of the electromagnetic spectrum. You can see in Figure 1 how the distribution increases before a sudden drop-off around a luminosity of -4.5. To prove this drop-off is real, the authors ran a few tests. They first looked for a correlation between the proper motion and the absolute magnitude. The goal here was to prove that a unbiased sample of white dwarfs was being used. If there was a correlation, it would indicate that the proper motion survey was missing the faintest white dwarfs, which would artificially cause the drop-off seen in Figure 1. Finding no correlation, the authors conducted the same test for M dwarfs from the same catalog. Finding no correlation either, they also confirmed that the M dwarf sample showed no shortage of stars between an absolute magnitude of 16 and 18, indicating that the drop off shown in Figure 1 in that range can be trusted.
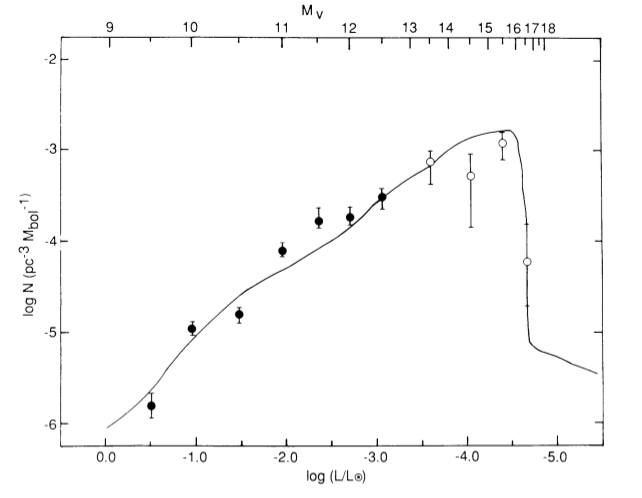
Figure 1: The luminosity distribution of white dwarfs. The abscissa shows the luminosity (bottom) and the absolute magnitude (top). The ordinate is the luminosity distribution, the number of white dwarfs per cubic parsec per absolute magnitude. The data points show the observed distribution while the line shows the accompanying theoretical calculation for the distribution.
The Theoretical Distribution
The authors then turned towards constructing a theoretical luminosity distribution that would match the observations. This model converts from a particular luminosity to an age. These models account for most of the relevant physics, including convection, Coulomb interactions, and crystallization and composition of the core of the white dwarf.
However, the reproduced luminosity distribution also depends on the mass distribution of white dwarfs. The mass distribution is important because the cooling rate depends on the surface area which can radiate away heat, and the surface area depends on the mass. White dwarfs are strange in that the more massive they are the smaller they get. So the most massive white dwarfs will cool the slowest. The authors used the currently known mass distribution, which peaks around 0.6 solar masses.
From these models, they produced the theoretical distribution which is shown as the solid line in Figure 1. This gives an age of the white dwarf population of 9.0 ± 1.8 Gyr.
Calculation of the Age of the Galactic Disk and Universe
To get the age of the Galactic disk, the amount of time white dwarfs spend on the Main Sequence must be added to the white dwarf age. The calculations above indicate that the dominant white dwarf mass at the drop off is 0.8 M⊙. Based on the available models of how much mass is lost going from the main sequence to becoming a white dwarf gives an initial mass between 2 and 4 M⊙ for these stars. The typical time for a star of that mass to be on the Main Sequence is 0.3 Gyr, giving the total age of the Galactic disk to be 9.3 ± 2.0 Gyr.
Finally, to determine the age of the universe from these calculations, the interval between the big bang and the formation of stars in the Galactic disk must be added. While there were many competing models of this time, they all gave an age around 1 Gyr. This gives a final age of the universe using white dwarf stars to be 10.3 ± 2.2 Gyr.
Implications
When this paper first appeared, it was unique in the way that it measured the age of the universe. While giving an age that was at the lower end of the currently debated ages, it made the strong point that the age of the universe was still up for discussion. As the first author recently told in an interview with NPR, the results presented in this paper were upsetting to some astronomers because it disagreed with their numbers.
Nowadays, the Planck satellite has measured the age of the universe to be 13.8 Gyr using the cosmic microwave background. And the value of Hubble’s Constant is about 71 km/s/Mpc. So while the results in this paper, as well as the values mentioned in the beginning, are off from the currently accepted value, the debate and process of determining the age of the universe is a good reminder of the workings of science. Multiple independent methods gave different results, which motivated astronomers to keep searching for a believable number.



Trackbacks/Pingbacks