Title: Testing the white dwarf mass-radius relationship with eclipsing binaries
Authors: S. G. Parsons, B. T. Gänsicke, T. R. Marsh et al.
First Author’s Institution: Department of Physics and Astronomy, University of Sheffield, UK
Status: Accepted to MNRAS [open access]
Look outside your window. Can you see the Sun? If it’s night-time, just pick a random star instead. Our Sun one day will become a white dwarf star, and the chance that the random star you’ve picked will follow the same path is over 95%. White dwarfs are by far the most common final evolutionary state for a star. The famous supernovas actually only occur when a star is massive enough to burn elements heavier than helium in its core, and that is usually not the case. What happens instead is that the star can only produce elements up to carbon and oxygen, and then nuclear reactions in the core cease to occur. With no release of energy to counteract the gravitational force, the carbon-oxygen core will contract more and more until it becomes degenerate. This degenerate core is essentially the white dwarf, which becomes visible when the outer layers of the star are ejected on its final breadth of hydrogen burning in outer shells.
What does it mean to be degenerate?
Degenerate matter occurs in stars when the density is so high that all the electrons are cramped in lower energy states. But there’s a catch: due to the Pauli exclusion principle, only two fermions, e.g. electrons, can occupy the same energy level. So other electrons end up in higher energy states and cannot move to already filled lower energy levels. This makes degenerate matter very resistible to compression, and is in fact what keeps white dwarfs from collapsing.
Degenerate matter has a really cool property: the pressure does not depend on temperature. This is because the kinetic energies of these electrons that cannot move to lower states of energy are quite high, and the rate of collisions between electrons and other particles is quite low, so the electrons essentially travel at the speed of light. The pressure on the gas depends on this speed. As the speed of light is the fastest the electrons can travel, adding heat will not change the pressure at all. This has an effect somewhat counter-intuitive. As the only way to increase pressure is by adding mass, when you increase pressure you also increase gravity and make the particles become spaced closer together, so the object becomes smaller. In other words, the more massive the white dwarf, the smaller its radius. As a consequence of this weird property of degenerate matter, there’s a relationship between a white dwarf’s mass and its radius, so that if you know one you can estimate the other and the other way around. But how accurate is this mass-radius relationship? Today’s paper authors decided to test!
Obtaining mass and radius independently
Despite being widely used, the mass-radius relationship remained untested observationally until this paper. That is because there aren’t many ways to estimate the mass of a white dwarf without relying on this relationship at some point. What the authors realised is that we can use eclipsing binary stars for that. Eclipsing binaries orbit in a plane which intersects our line of sight, allowing us to detect dips in light when the stars transit in front of each other. For these objects, we can combine photometric and spectroscopic measurements to estimate the mass and the radius independently.
The shape of the eclipses of the white dwarfs by their companions, which in this paper are all main-sequence stars, gives us two pieces of information: the width and the duration of the eclipses. However, there’s an issue: we have three unknown quantities, namely the orbital inclination and the radius of each star. So we need one more piece of information to be able to determine all the unknowns.
The authors suggest different methods, but what works best in their sample is to use the gravitational redshift estimated from spectroscopy. As the gravity in white dwarfs is really high (about 350,000 times the gravity of Earth!), light gets shifted a measurable amount towards the red when it exits the white dwarf, as it was delayed. The amount of redshift depends on the mass and radius of the white dwarf. Combining that with Kepler’s third law, we obtain a relationship between the white dwarf’s radius and the binary inclination. All we need is to estimate the radial velocity semi-amplitudes for both stars, hence the necessity of spectroscopy, which was also used to constrain the effective temperature of the white dwarf. Going back to Kepler’s third law with the estimated inclination, we can also estimate the mass of the white dwarf.
So the combined fit of the light curve and the radial velocities of both stars, together with Kepler’s law and the known relation for gravitational shift, give us the mass and the radius without having to recur to the mass-radius relationship. Just the independent measure we needed!
The results
Figure 1 shows the comparison between the values the authors obtained with the theoretical models for different temperatures. Black lines are for the more common C/O core white dwarfs, while green lines are for white dwarfs with a He core. He-core white dwarfs are less massive and are formed when the outer envelope is lost by the progenitor star before helium is even ignited. They would be formed by lower mass stars that do not achieve conditions to burn helium, but the Universe is not old enough for them to have evolved off the main sequence just yet, so this objects are explained by some form of enhanced mass loss (such as binary evolution). As the analysed white dwarfs have different temperatures and core compositions, is difficult to define how the results agree with the theory based on this figure.
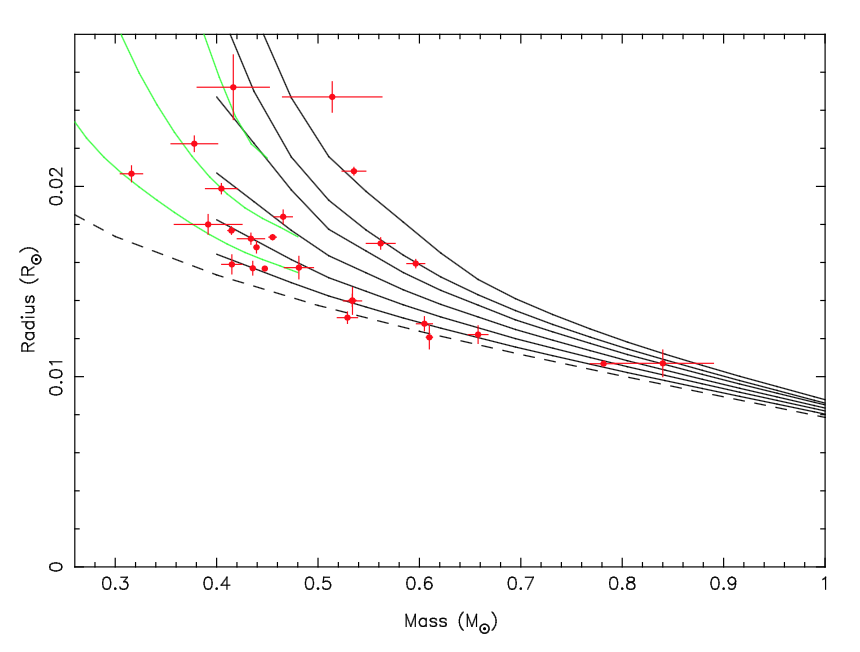
Figure 1: Comparison between mass and radius obtained from observations, represented by the red data points, and theoretical mass-radius relationships for different effective temperatures. Black lines assume a C/O core and green lines assume a He core. [Adapted from figure 9 in the paper.]
Instead, the authors analyse what we see in Figure 2, which is the ratio between the radii estimated observationally and using the mass-radius relationship as a function of mass. Below 0.5 solar masses, the authors assume both a relationship assuming a He core and a C/O core. The first result is that white dwarfs with masses below 0.5 solar masses are more consistent with a He core, which agrees with our theories of stellar evolution. However, this is the first time we have direct observational evidence for that.
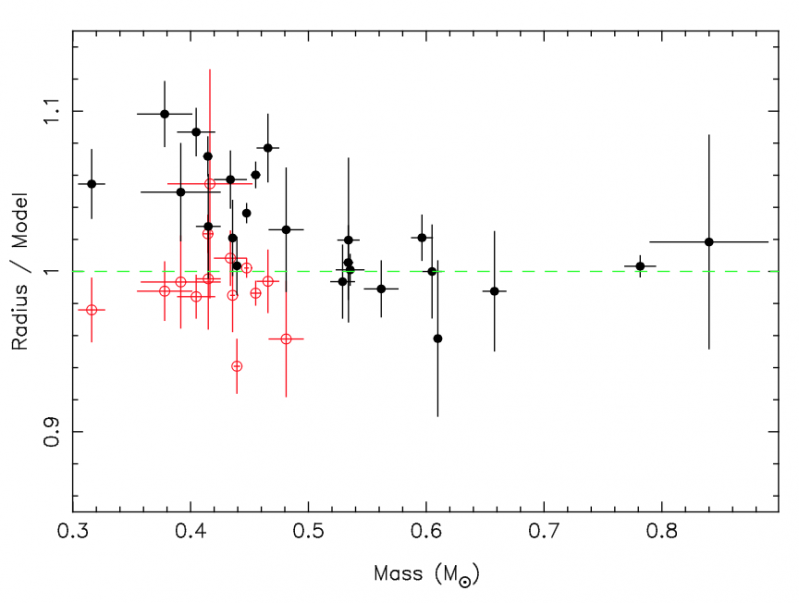
Figure 2: Ratio of the estimated white dwarf radii to theoretical predictions as a function of mass. Below 0.5 solar masses, black points assume a C/O core white dwarf and red points assume a He core white dwarf. Almost all radius measurement at this range are more consistent with He core. [Figure 10 in the paper.]
Another interesting test the authors made was to compare surface gravities obtained from their fit to the spectra and derived from the mass and radius obtained from the light curves. Fitting spectra is the most widely used method to obtain the physical parameters of a white dwarf, so testing this independently is important to check we are basing our science in correct estimates. As Figure 3 shows, in most cases there’s excellent agreement between the results, but there are a few outliers where the spectral fit overestimates the gravity. In most of these cases, this disagreement can easily be explained by contamination from the companion. There’s one exception where the white dwarf dominates the spectrum so contamination from the companion is not enough to cause the discrepancy, but for this one the discrepancy is only at a 2-sigma level. Additional broadening mechanisms, such as magnetic fields, might be the cause for that.
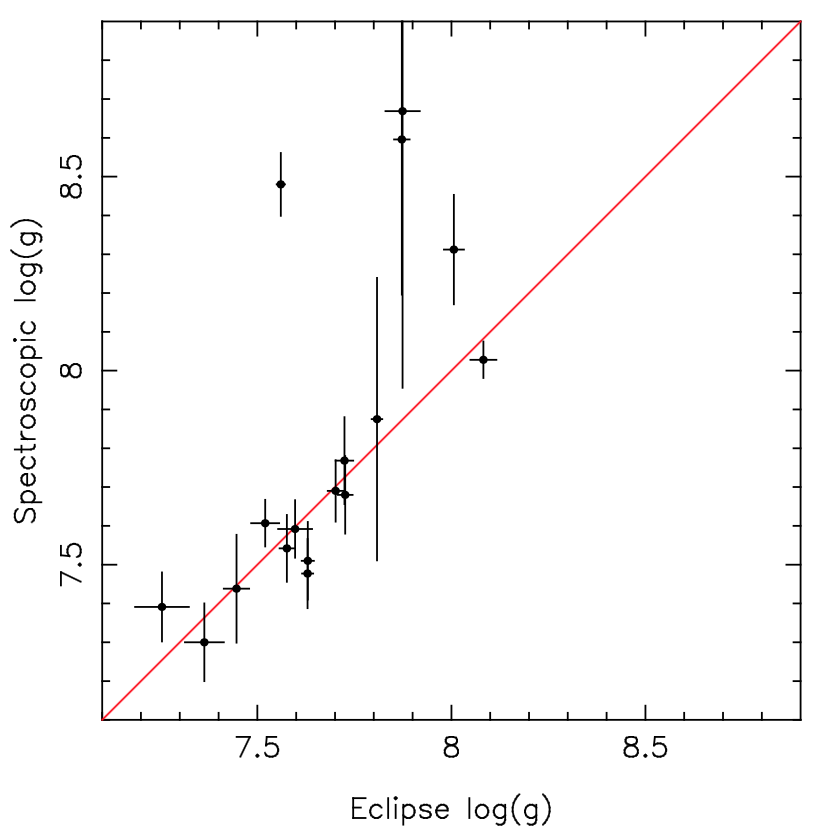
Figure 3: Comparison between surface gravities estimated from spectral fits, and those computed from the mass and radius values obtained from the light curves. [Figure 13 in the paper.]
Why does it matter?
The authors came to conclude that both our mass-radius relationship and spectral modelling are quite good at estimating the properties of white dwarfs. This result is important not only for those directly interested in white dwarfs, but has also implications for cosmology. The radius of a white dwarf is related to its cooling rate, which depends on its surface area. As you can read on this bite, the cooling times of white dwarfs can be used to estimate the ages of different stellar populations. The mass-radius relationship also sets an upper limit to the mass of a white dwarf, which is an important result to the study of type Ia supernovae, which in turn are used to measure the expansion of the Universe.
Now that we know that our theoretical models are doing a good job, we can keep doing cool science with them!



Trackbacks/Pingbacks