Title: A Predicted Astrometric Microlensing Event by a Nearby White Dwarf
Authors: P. McGill, L. C. Smith, N. W. Evans, V. Belokurov, & R. L. Smart
First Author’s Institution: Institute of Astronomy, University of Cambridge
Status: accepted to MNRAS Letters (open access on arXiv)
White Dwarfs (WDs) are pretty incredible objects. For starters, most of the stars you know will become WDs. The Big Dipper? All of its stars are on track to become WDs. The North Star? Another future WD. Oh, and our very own Sun? You guessed it! On the sure path to White Dwarf-dom.
But WDs aren’t awesome just because they are common. They also seem to defy basic logic: the more massive they are, the smaller they become! This mind-bending fact is a direct consequence of the reason they exist in the first place: electron degeneracy pressure (here’s a broader review of how WDs form). Back in the 1930s, Subrahmanyan Chandrasekhar derived the basis for the currently accepted mass-radius relation for WDs (see figure 1), which also led him to calculate what is known today as the Chandrasekhar limit, or M=1.41 Solar masses, above which a WD cannot exist. In reality once this mass limit is reached, the WD explodes in a type Ia supernova. (Quick aside: for those of you deciding how to travel to your next conference, note that Chandrasekhar did much of this work while travelling from India to England by boat).
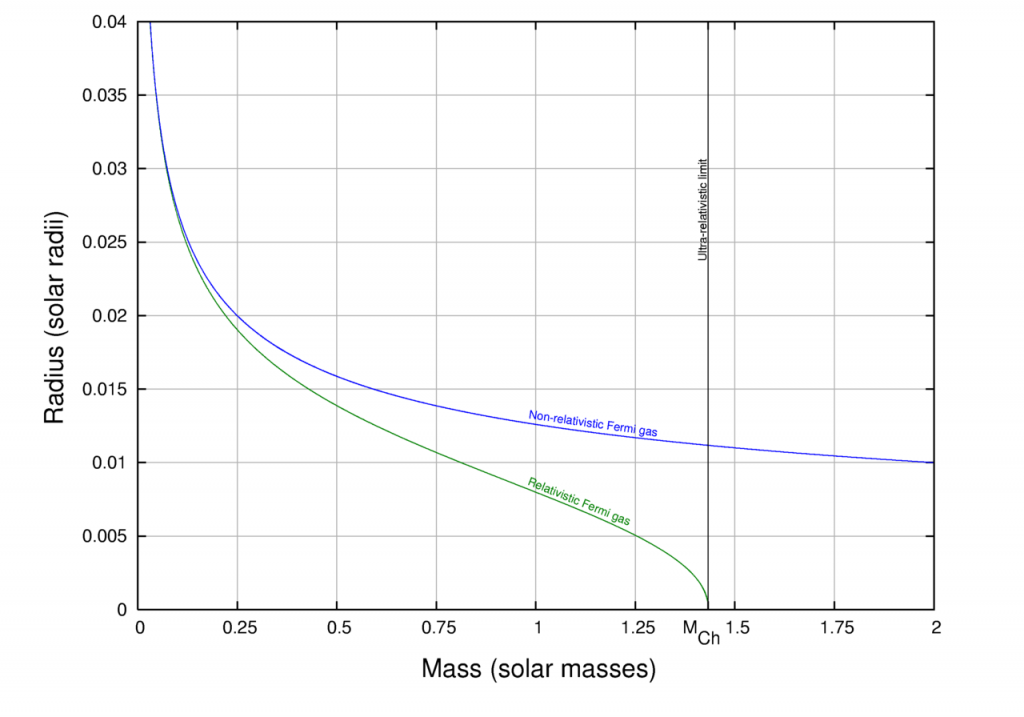
Figure 1. Chandrasekhar’s critical correction to the WD mass-radius relation, which took into account the effects of relativity and predicted the upper mass bound for WDs at 1.41 Solar masses. Chandrasekhar’s model is plotted in green compared to the previously accepted non-relativistic model in blue (credit: Wikimedia Commons).
We know nowadays that the mass-radius relation (MRR) is a bit more complex than Chandrasekhar’s initial formulation. Complicating factors include the fact that WDs aren’t fully degenerate like Chandrasekhar assumed (for instance, some are known to have dense atmospheres of non-degenerate Hydrogen or Helium), and they are expected to behave differently in isolation than they do when found in a tight binary. These complications lead to variations of up to 15% between different MRR models.
The obvious way to resolve these discrepancies is to measure the masses and radii of a bunch of WDs in both tight binaries and in isolation and compare them to theory. Unfortunately, this turns out to be exceedingly difficult. Most ways of measuring the masses of WDs rely on theoretical assumptions and empirical models of WD structure, which in turn rely on knowing the radius of the WD, so they aren’t much help here. One of the most successful attempts at obtaining independent measurements to date made use of WDs in eclipsing binaries (check out this Astrobite!), but as mentioned before, WDs in binaries are expected to behave differently than those in isolation. The challenge, therefore, is to find a way to measure the mass of a WD in isolation.
Microlensing to the rescue!
One of Einstein’s first predictions from general relativity was that light should bend around massive objects like stars. This quickly turned from a hypothesis into one of the first triumphs of relativity when Arthur Eddington confirmed Einstein’s prediction during the solar eclipse of 1919 (see figure 2). The term Microlensing is used nowadays to describe the bending of light around stars or compact objects like black holes, neutron stars, or WDs.
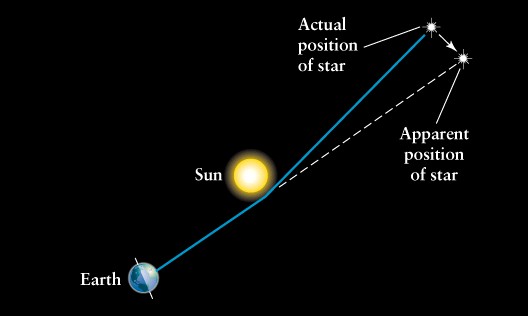
Figure 2. The effect of gravitational lensing due to the Sun’s distortion of space-time on the trajectory of photons from a distant star, and the resulting shift in the apparent position of the background star as viewed from Earth (image credit: Andy Bohn).
So how does microlensing help with our WD mass conundrum? Einstein used the well-known mass of the Sun to predict how the image of a background star would shift due to lensing – so all we need to do is reverse the logic. If we can find a WD that happens to pass right in front of a background star, and if we can measure by how much that background star’s apparent position shifts due to gravitational lensing, we can use this to determine the mass of the WD.
There’s just one slight problem with this approach: you have to find a nearby WD which passes almost directly in front of a far away background star. And to make matters even worse, you need a telescope that’s sensitive enough to pick out the position of the background star when the much brighter lensing WD is almost exactly in front of it.
A one-in-13,000 opportunity
The authors of today’s paper used the Tycho-Gaia Astrometric Solution catalogue (aka TGAS) which provides very high-accuracy velocity data for potential lens stars, and cross matched it with all of the stars in the Gaia Data Release 1 (DR1) source catalog to find any microlensing events that would happen within Gaia’s remaining lifetime. After combing through over 13,000 candidate lens stars, the authors were able to find one promising microlensing event for Gaia to detect! It turns out that we’re in for a treat on November 11th, 2019: LAWD 37, one of the closest known WDs to the Sun at only 4.6 parsecs away, will pass within a fraction of an arcsecond of a background star (with the somewhat less catchy name: Gaia Source 5332606346467258496), as shown in figure 3.

Figure 3. The candidate WD LAWD 37 approaching the background source star over the past two decades. Left: an image from SDSS from 1998. Right: an image from the Dark Energy Camera from 2016, showing the WD much closer to the background source. The blue dotted line in the inset shows the expected trajectory of LAWD 37 (the wavy up-and-down motion is due to the Earth’s parallax!). They are expected to reach closest approach on November 11th, 2019 (Figure 1 from the paper).
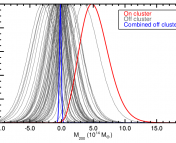
The authors calculated that this encounter should cause the apparent position of the background source to shift by about 3 milliarcseconds (see figure 4) – a shift big enough for Gaia to detect (if you’re thinking that 3 milliarcseconds sounds really small – you’re right. It’s about how big a typical pickup truck would look from Earth if you parked it on the Moon). With this data, we should be able to determine the mass of LAWD 37 to within 3%, providing us with our desired test of the MRR of WDs in isolation.
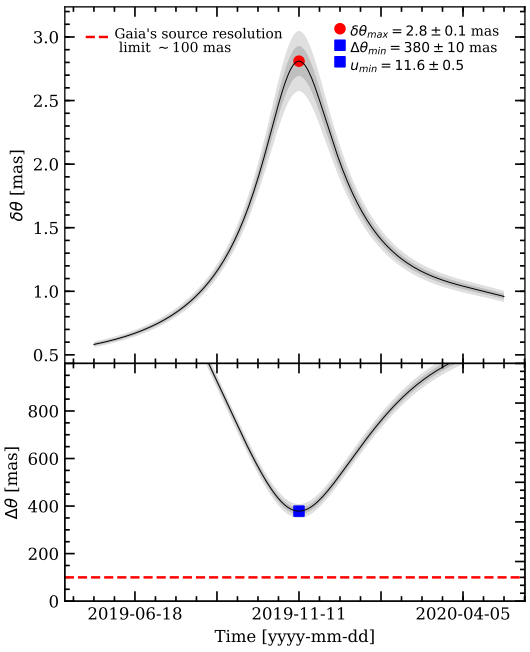
Figure 4. Top: the shift in the apparent position of the background star as a result of the gravitational lensing by LAWD 37, as a function of time. Bottom: the angular separation between the background source and LAWD 37 (Figure 2 from the paper).
So hopefully by now you’ve marked your calendar with “WD microlensing” on November 11th, 2019 (assuming you won’t be too busy watching this). But aside from this specific finding, today’s paper also demonstrates the power of using microlensing to measure precise masses of astronomical objects. Thanks to Gaia’s recently published second data release (DR2) from April 25th, we expect to be able to identify many more candidate microlensing events, allowing us to make precise and independent mass measurements for a wide variety of stars and compact objects. Testing the famous WD MRR is just one example of many exciting applications these measurements could have.