Title: KIC 2856960: the impossible triple star
Authors: T.R. Marsh, D.J. Armstrong, and P.J. Carter
First Author’s Institution: University of Warwick, Coventry, UK
Status: Accepted to MNRAS
Binary stars are extremely common in the universe, and many of them further reside in triple star systems. Further, because of the close orbits of many binary systems, they are often observed to eclipse, which gives astronomers extremely detailed information on both stars. However, third stars in triple systems tend to be at longer orbital separations, lessening the likelihood of all three bodies eclipsing. But thanks to Kepler’s continuous coverage, a number of multiply eclipsing triple systems have now been observed. KIC 2856960 is one of them—or is it?
KIC 2856960 was first identified as a binary system in 2011, with the main pair eclipsing every 0.258 days. But in 2012, a secondary, deeper dip was found, which lasts about one day every ~204 days. This “dip” is actually the complicated series of dips seen in Figure 1, as the close binary passes in front of some other object. These dips could have been caused by a planet orbiting the binary system, but in 2013, a different group proved that the third object must be a star. They did this by finding variations in the orbital period of the binary, variations caused by the changing light travel time as the binary orbits a third star.
No one had attempted to model what the orbits, masses, and radii of these three stars could be to match the observed light curves from Kepler, and so the authors of this paper dove in.
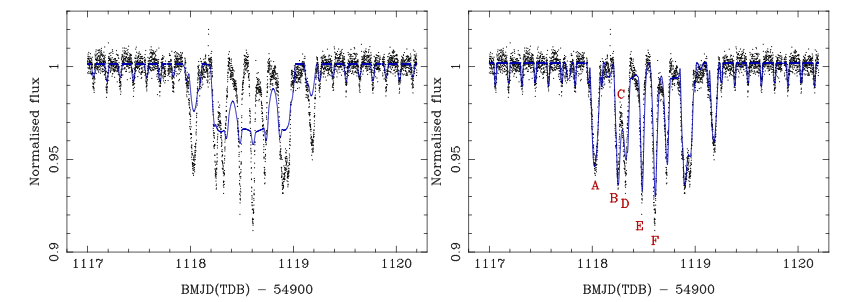
Figure 1. Kepler light curves shown in black, both panels. Models are shown in blue. The small variations on the edges are the close binary’s eclipses, while the larger dips in the middle are due to a geometrically complicated scenario where the binary crosses a third star. The left panel shows the best fit triple star model, which is a poor fit. The right panel shows the same basic model, but ignores Kepler’s laws. This produces a much better fit, but has the unfortunate drawback of breaking the laws of physics. Credit: Marsh et al., 2014.
Because the binary eclipses so many times, yielding extremely precise data, the authors focused only on the binary’s orbit at first, ignoring the large dips. They explained that they hoped to lock down as many parameters as possible for the binary system, leaving less parameter space to explore when they moved on to the triple. They were able to improve on past work, partially due to the accumulation of more data as Kepler continued to observe, but mostly thanks to short cadence Kepler data unavailable to previous groups. They strongly confirmed the earlier findings that the binary is in orbit around a third star.
The authors next attempted to model a triple star system, but found that even their best fit is quite poor (see Figure 1, left panel). It is also astrophysically impossible, yielding a radius for one of the stars of 1.29 R☉ (reasonable), but a mass of 10-5 M☉ (impossibly small density; this star would completely overflow its Roche lobe). The authors did manage to achieve a statistically good fit (Figure 1, right panel), but only if they ignored Kepler’s laws. This is, of course, also physically impossible, but they argue that this “solution” allows them to qualitatively investigate the problems with the triple star solution. Specifically, it shows that the data requires a longer binary separation than is physically possible in the three star model, especially to explain the double dips labeled B-C-D in Figure 1, and repeated at roughly 1119 on the x axis. Put very simply, the dips last too long for any physically possible three star system.
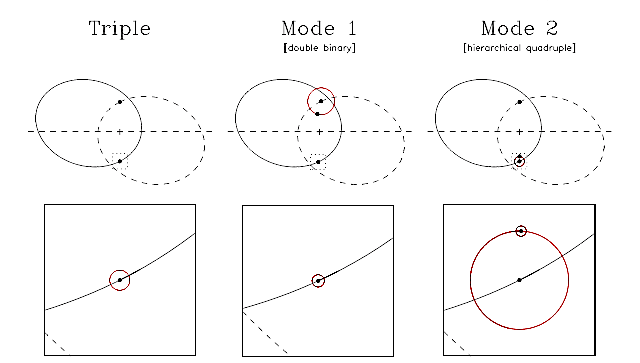
Figure 2. Three different orbital modes considered in this paper. In all cases, the observer is located at the bottom of the figure and plus signs indicate the center of mass of the system. The lower panels are a 10x magnified view of the dotted box, centered around the close binary. In the left two panels, the orbit of the center of mass of the close binary is shown by the solid ellipse. In the left panel (triple system), the orbit of star 3 is shown by the dashed ellipse. In the middle panel (double binary), “star 3” is a second binary, and the dashed ellipse shows the orbit of the center of mass of that binary, with the red circle showing the orbit of “star 3” around a fixed point on the ellipse. The right panel shows a hierarchical system, where the close binary (orbit given by the tiny red circle in lower panel) orbits a third star (orbit given by the large red circle in lower panel/red circle in upper panel), and this triple (moving on the solid ellipse) in turn orbits a fourth star, (moving on the dashed ellipse). Credit: Marsh et al., 2014.
A way around this problem is to introduce a fourth star into the model. Either “star 3” can be replaced by a second binary, or the first, close binary can orbit a third star, and that triple system can in turn orbit a fourth star. This second method is called a hierarchical quadruple. Both models have the effect of slowing the relative speed between the close binary and the more distant star, allowing the long transit time seen in the Kepler lightcurves. See Figure 2 for a representation of these different model scenarios.
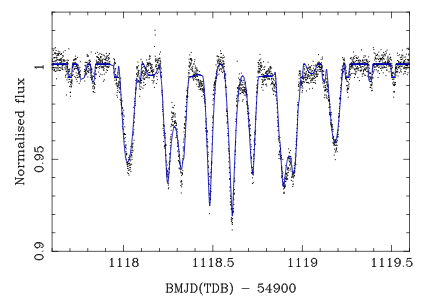
Figure 3. Best fit quadruple model plotted in blue over black lightcurve data. This model additionally allows the epoch of the close binary to vary, which improves the fit, but results in the close binary model eclipses arriving too early compared to the data. Credit: Marsh et al., 2014.
These quadruple models yield reasonably good fits to the data, and are physically possible, which is an improvement over the triple model! The double binary model provides slightly more reasonable results than the hierarchical model. But the authors caution that there are still unresolved problems. First, the models yield uneven radii for the stars in the close binary (2.5-4x difference in radius). This is a problem because the lightcurve depths indicate that the two stars must be of similar brightness, so it is hard to imagine a scenario where these two unevolved, low-mass, main sequence stars end up with such different radii. Another problem is that even the best quadruple model fit is not a great fit to the data. By opening up more parameters (remember that the authors originally fixed the close binary’s orbital parameters based on data excluding the big dips), they achieved a better total χ2, but at a cost: the close binary’s model eclipses now arrive too early when compared to the data (see Figure 3 for their best fit, though the scaling means the eclipse timing offsets aren’t really visible on the plot).
The authors admit that even their best model cannot tell the whole story of this system. But it’s a pretty interesting story so far!




Has it been considered whether the fourth body could be a planet? If it has not eclipsed any of the other three, can we be sure that it is a star?