Title: How low can you go? The photoeccentric effect for planets of various sizes
Authors: Ellen Price, Leslie Rogers, John Johnson, Rebekah Dawson
First Author’s Institution: California Institute of Technology
I often think that all 3,000+ exoplanets that have been discovered are a lot like most people’s facebook friends. C’mon… Do you actually know all 3,000 of them? But who can blame you. You met them once years ago and now there isn’t enough time in a day or month or even in a year to comb through everyone’s profile and figure out whom you care about and whom you don’t. Well it seems like exoplanet scientists are having a similar problem. According to the Exoplanet Orbit Database, there are 3,303 planet candidates. For planet candidates, the following is true:
- The Kepler Mission has observed each planet passing in front of its parent star and has obtained a light curve (see transit method)
- From each light curve, scientists can determine each planet’s radius and orbital period
- Additional observations must be done in order to confirm each planet’s existence and/or to get additional planet properties.
A planet’s radius and orbital period gives us about as much information as looking at someone’s profile picture. You get a general feeling for it’s size and hotness. Ideally, though, we’d like to know how dense the planet is, and how it moves around its parent star. For that, bullet #3 indicates we’d need additional observations. Like vetting through facebook friends, it’s just not practical or physically possible to try and follow up all 3,000+ planets to determine whom we care about and whom we don’t. In fact, for some of the more distant Kepler planets, not even the world’s largest telescopes could obtain data with high enough precision to derive a parameter such as orbital eccentricity. Therefore, it would be infinitely more practical if we could figure out a way to strip out more than just planet radius and orbital period from the Kepler light curves. In today’s astrobite, Price et al. do just that by discussing a new technique to determine eccentricities of planets from Kepler transiting exoplanets, which they have coined the “photoeccentric effect”.
Photoeccentric Effect
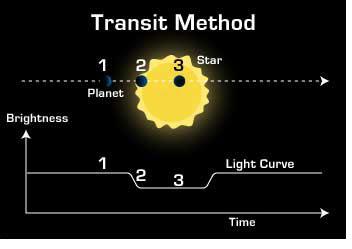
Figure 1. Cartoon drawing of the transit method taken from JPL. The numbers above represent key states in a transit when the planet is 1) out of transit, 2) in ingress 3) in transit. If we kept going, (4) would be in egress and (5) would be out of transit again. Because the light curve is a function of time, we can measure the time spent in each of these phases.
For those who are new to the transit method let’s quickly revisit some jargon. Looking at figure 1, there are three main events we want to internalize: 1) before the planet approaches the star it is “out of transit”, 2) when the planet is passing into/out of the disk of the star, it is in “ingress/egress” and 3) when the planet is in front of the star it is “in transit”. The planet in figure 1 has a perfectly circular orbit (zero eccentricity). Now, imagine stretching the planet’s orbit toward you in attempt to increase the eccentricity and think about how that might affect the planet’s light curve. As it turns out (and like everything in life), those slight deviations in the light curves can be described by a set of equations and voilà! The photoeccentric effect was born. Well… Not that easy. A little more magic is required to actually figure out the eccentricity from the equations. The good news is, this technique was proven to work on Kepler’s biggest (think jupiter-sized) planets two years ago by two of the authors on this paper (Dawson & Johnson). Price et al. take that same technique and try to figure out if we can pin down eccentricities of some of the smallest sized planets. Because let’s face it, those are the only ones we care about anyways (kidding!!).
Methods
In order to calculate the eccentricity, Price et. al. define a parameter, g, which describes how much a light curve deviates from the ideal, circular-orbit light curve shown in Figure 1. The parameter, g is a function of eccentricity, e, and ω, the argument of periastron (g(e, ω)). It is also a separate function of six different parameters we should be familiar with by now: transit depth, ingress/egress duration, transit duration, orbital period, radius of the star, semi-major axis of the planet (g(δ, τ, T, P, R*, a)). Now we have two equations and eight unknowns. So what do we do? Cry? No! Because we already said that δ, τ, T, P, R*, and a can all be measured directly from the light curve and our parameter g, can be determined. Now we just have one equation g(e, ω) with two unknowns. Price et. al. use Bayesian statistics to nail down the eccentricities. I refer the reader to this astrobite, which gives a great break down of Bayesian statistics for those that are interested.
Results
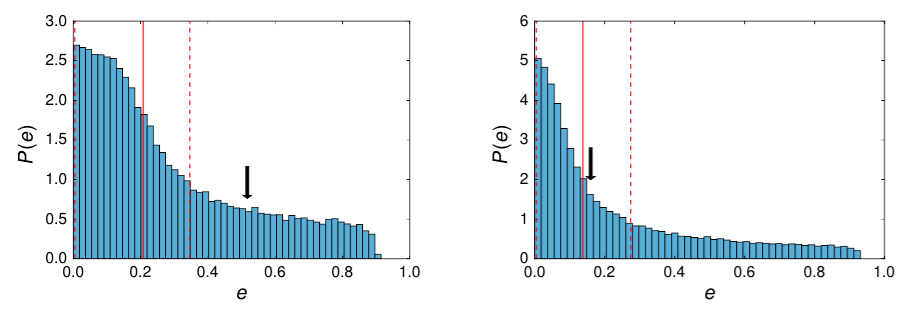
Figure 2. To the right are the results for HAT-P-2b and to the left are the results for GJ 436b. P(e) is the posterior probability distribution (see Bayesian statistics). The arrows represent the known eccentricities for each planet and the red dashed lines represent the range of statistically viable eccentricities derived from the Price et. al. model. If the model worked correctly, the measured value should fall somewhere in between the red dashed lines. Main point: Price et. al. accurately determines eccentricity for GJ 436b but not HAT-P-2b.
Price et. al. find that for smaller and smaller planets, the uncertainty in their calculation of eccentricity increases. Why is this? Well, for smaller and smaller planets, the light curve starts to resemble a useless flat line and it gets more and more difficult to determine δ, τ, T, P, R*, and a. And because we used those parameters to determine g, it directly effects our calculation of eccentricity. Figure 2 shows results for the cases of two different planets: HAT-P-2b (left) and GJ 436b (right). In both figures the arrow indicates the known value of the eccentricity. If our statistics was correct, the measured values should lie within the red dashed lines, which represent statistically viable solutions of the eccentricity. Therefore, Price et. al. were able to get eccentricities for GJ 426b but not HAT-P-2b. They ultimately find that their method works well for both very large eccentricities and very small eccentricities (GJ 436b has a low eccentricity), but not well for intermediate eccentricities (HAT-P-2b).
In the end this is a fantastic result. We are one step closer to unraveling the wealth of information that might be hidden deep within our 3,303 facebook friendly exoplanets.