Title: Atmospheric Mass Loss During Planet Formation: The Importance of Planetesimal Impacts
Authors: H. Schlichting, R. Sari & A. Yalinevich
First author’s affiliation: MIT
Paper status: submitted to Icarus
Earth and its Atmosphere
Do you know what the mass of Earth’s atmosphere compared to the planetary mass is? It’s about one in a million. Only one in a million. In comparison, Venus – often called Earth’s sister planet, because it is very similar to Earth in mass and radius – has an atmosphere-to-planet ratio of about ten thousand. As a curious Astrobite reader, you might be thinking: “Interesting. Go on and tell me the reason for it!” At this point, I have to disappoint: there is no clear answer to the question yet. Nevertheless, there are multiple hypotheses. An attractive explanation is that Earth’s atmosphere used to be more massive in the past – as suggested by Venus’ atmosphere – but was depleted later. The authors of today’s featured paper assume that impacts of the Earth by small objects caused a reduction of the atmosphere’s mass. The exciting part of their work is that they figure out what size of impactors are potentially best in reducing the atmosphere. If you are curious about the physics behind their study, read the next paragraph; if you only care about their result, go straight to the conclusion. (Warning: you will miss some useful conceptual considerations that are relevant for exoplanets as well.)
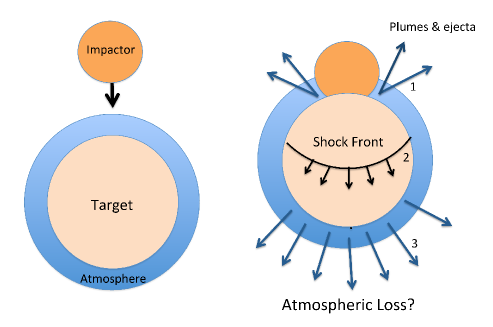
Figure 1: Impact of a massive object impacting a planet. After the collision, atmospheric mass is lost close to the impact as well as on the other side through a global shock propagating through the planet.
Large and small impactors trigger different forms of atmospheric loss
The authors seek to get a rough estimate of the best impactor size based on the dominant processes and under several assumptions, without getting lost in too many details. Let’s go through the fundamental scenarios that can happen step by step. If you want to eject mass from an atmosphere through a collision, the impactor must pass through the atmosphere and reach the surface of the planet. It is known from previous studies that the relevant physical quantity in this process is momentum, and thus mass and velocity. Impactors would have a distribution of velocities, but neglecting higher velocities is fine for their purpose of a rough picture.For simplicity, the authors assume the same velocity for all impactors of roughly the threshold velocity not to be captured by the gravity of the planet (the so called escape velocity ). The chosen velocity is motivated by the fact that most objects with masses much higher velocities would just fly by the planet. The impactors must have a minimum mass
to eject part of the atmosphere. By assuming that the impactors are of similar density
and using
, they reformulate their expression in terms of minimum size
. Objects have to be at least
in radius, otherwise they are destroyed in the atmosphere before they can hit the ground.
Now, there are giant and small impacts. In Figure 1, you can see a sketch of an impact with a massive object that produces a giant impact. The impactor passes through the atmosphere, collides with the surface and ejects material close to the location of impact. To simplify the calculations, the authors assume that the entire atmosphere has a constant temperature (physicists say the atmosphere is isothermal) and that no energy is “lost” by heat in the flow through the atmosphere (in physical terms, the process is adiabatic.) In the sketch, the impactor is so massive that it induces a strong shock that travels through the entire planet and causes a loss of the atmosphere on the other side of the planet. This scenario is called global atmospheric loss. In contrast, smaller impactors are not strong enough to induce a shock propagating through the planet. They cannot cause a loss on the other side, and only produce a local loss close to the impact location as seen in Figure 2. Although a single small impact ejects less mass from the atmosphere, the sum of many small impacts could produce significant total mass loss. Taking into account the above assumptions, an interesting question is: what impactor size causes the highest atmospheric mass loss compared to the impactor’s mass? To test this, the authors consider impacts of fixed size and study how much total mass in impactors is needed to get rid of the entire atmosphere.
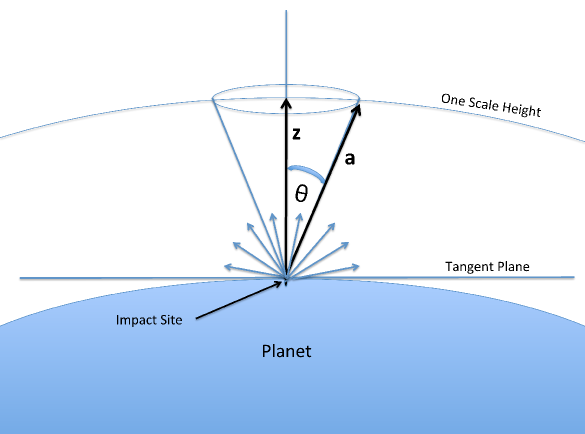
Figure 2: Illustration of mass loss by an impact with a small body. Assuming all impacting bodies have the same density, but different sizes, the larger ones are more massive. The relevant distance to consider for loss is the distance between the location of impact (impact site) from the reference height of the atmosphere (scale height). The larger theta is, the larger the distance becomes and the more mass and correspondingly a larger radius is needed to eject mass in that direction.
What do they find out, what does it mean?
Surprisingly, they find that small objects that are km in radius, which is only slightly larger than the minimum size to eject part of the atmosphere (
), are most efficient in reducing the atmosphere (see Figure 3). Based on this result, the authors suggest that Earth lost most of its atmosphere while it was still forming, when plenty of small km-size bodies flew around and impacted the Earth. According to the authors it could very well be that today’s atmosphere mass corresponds to the equilibrium between the delivery of new material to Earth by small objects and the amount of mass that got ejected by small impacts. Also, the relatively small amount of material ejected from the planet by these small bodies could also explain why there are no signs of a global magma flow, which would be expected if the atmosphere got lost during a giant impact. To summarize, it is fair to say that – regardless of whether this happened in Earth’s atmosphere – it is certainly interesting that small impactors are so efficient in ejecting planetary atmospheres. With respect to the young field of exoplanetary (atmospheric) science, it contributes an important new aspect to take into account for explaining the formation of planetary systems. Future studies could test whether the results change with different impact speeds and impactor sizes.
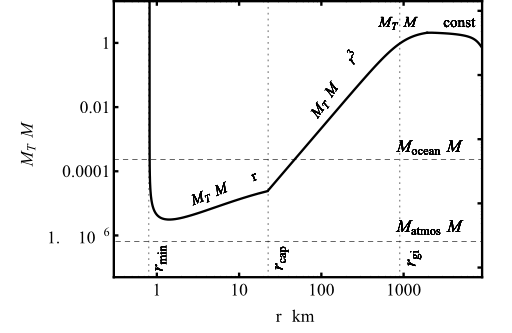
Figure 3: Total mass needed to eject the entire mass of the Earth for objects of different size. Interestingly, objects only a little bit larger than the minimum size are most efficient in ejecting the atmospheric mass.