Title: The galaxy luminosity function at z ~ 6 and evidence for rapid evolution in the bright end from z ~ 7 to 5
Authors: R. A. A. Bowler et al.
First Author Institution: SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh EH9 3HJ, UK
Status: Published in MNRAS, 451, 1817
A lot of the time Astrophysicists might use some fancy computing and equations to figure out things about the Universe – but sometimes just counting the number of galaxies you can see, can tell you a whole lot more. You can turn the number of galaxies you can see in a certain area of sky into a number density and then look how this value changes with increasing stellar mass (or luminosity) of a galaxy (i.e. how bright a galaxy is and therefore how much mass it has in stars). Astronomers call this the luminosity function (LF) and it’s really important if you want to get a handle on how galaxies have been built up over time.
We can also get an estimate of the LF from simulations that try to emulate the Universe. Comparing both the observed and simulated galaxy number densities tells us how well our models of what shapes the Universe perform. Our most accepted model of the Universe is λ Cold Dark Matter (λCDM) where the Universe contains a cosmological constant, λ (i.e. dark energy) and cold dark matter (cold to represent their minimal energy). However λCDM does not give us the same number density of galaxies as observed at all stellar galaxy masses. It overestimates the numbers of galaxies at the extremely low mass and extremely high mass end of the LF. People have tried to explain this discrepancy in many different ways. For example at the low mass end it’s thought that this is caused by what astronomers call a selection effect – that the galaxies should be there, but they’re so faint that there’s no way we can currently detect them. We don’t have that excuse at the high mass end though, as these galaxies are really bright, so they’d be hard to miss. But one thing that isn’t included in the simulations is feedback of energy from AGN (active galactic nuclei – i.e. active black holes in the centres of galaxies) which can throw out or heat gas needed for star formation in a galaxy. This feedback can stop a galaxy from growing overly large in mass, so people have argued that the inclusion of this in the simulations removes the discrepancy with observations.
Studying this problem locally with galaxies that are nearby is relatively easy compared to trying to get this LF for galaxies at high redshift, because even the brightest galaxies at huge distances are hard to detect. Getting accurate estimates for their number counts is therefore really difficult, especially if we want to study how the LF changes with increasing redshift (i.e. increasing distance and therefore looking further back into the Universe’s past). The author’s of this paper have been tackling this problem of getting accurate number counts for galaxies at z > 6 (in the first billion years of the Universe’s life) by using two ultra deep surveys of the sky in the infra-red: COSMOS and UDS. They found 266 candidate galaxies (after removing possible contaminant sources that look like galaxies at big distances, such as brown dwarf stars in our galaxy) all within a redshift of 5.5 < z < 6.5. Using these galaxies and other results from previous publications, they looked at how the LF changes from z= 5 to z = 7 (over 500 million years of the Universe’s history) , which is shown below in Figure 1.
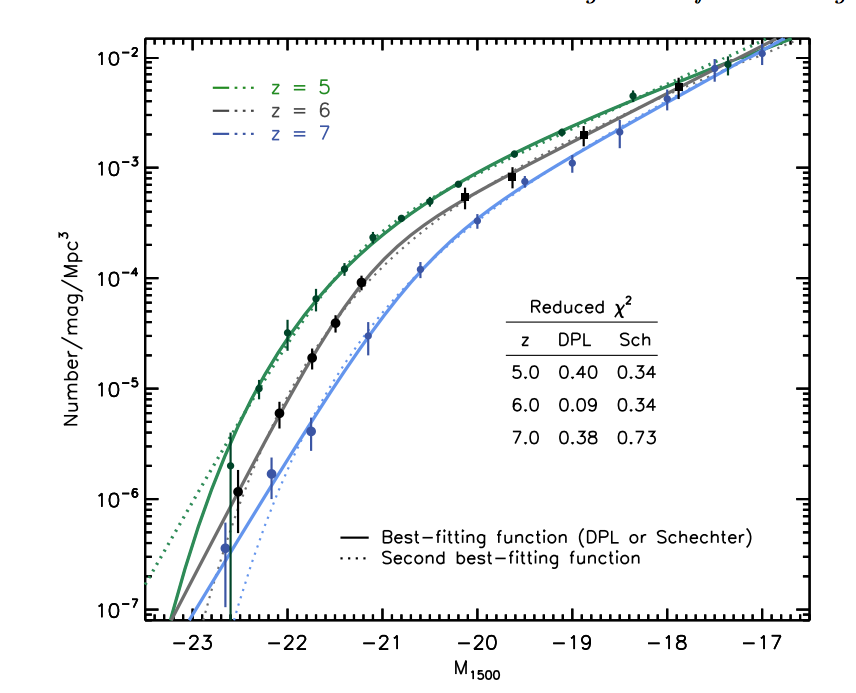
Figure 1; The y-axis shows the number density of galaxies at a given infra-red magnitude on the x-axis. Bright, massive galaxies are on the left of the plot and faint, small galaxies are on the right of the plot. The different coloured lines show how the LF changes with increasing redshift.
What’s cool about Figure 1 is that it shows that, at the faint end (), the LFs at the three different redshifts are extremely similar; whereas at the bright end(
) the three differ quite significantly. The authors argue that this could be because the AGN feedback that’s thought to affect the bright end of the LF in the local Universe has less of an effect with increasing redshift (i.e. decreasing age of the Universe). At such early times in the Universe’s life (z=7 is only ~700 million years after the Big Bang) black holes haven’t managed to grow and accrete sufficient material to be powerful enough to output enough energy to feedback on the star formation of a galaxy. As the Universe ages, black holes keep growing, eventually become active, so that AGN feedback becomes a big influence on the numbers of super massive galaxies at the bright end of the LF. This is a really intriguing idea, one that needs to be looked at further with the advent of deeper and wider surveys of the sky in the future, such as those using ALMA and the JWST. So watch this space!





“The author’s of this paper” should read “the authors of this paper”.
It troubles me that, possibly with increased reliance on predictive text and spell checkers, this kind of error is becoming more common.
One of the astrobites team notes that she likes Oxford commas – I join her in that, and further add that, like this rescue agency for mistreated apostrophes
http://freetheapostrophe.com/the-plight-of-the-apostrophe/, I am FANATICAL about the correct use of the apostrophe.
http://www.scribendi.com/advice/using_apostrophes.en.html
Hello Becky,
Nice post. I was wondering what does the 1500 subscript in the figure one for the absolute magnitude M (if I am correct that this is absolute magnitude) refer to?
Andrija
Since it is an “infra-red magnitude” I would guess that it is the center wavelength (in nm) of the chosen filter. IR is 700 – 1 000 000 nm.
[Disclaimer: I am not an astronomer,]
M_1500 refers to absolute magnitude at rest-frame 1500 Angstroms (150 nm in the UV, redshifted by a factor of 5,6,7 into red or near infrared as observed).
What worries me most is the Figure 1 plot’s consistently low values of reduce Chi-square (along with the bin sizes that cover a range of an order of magnitude vertically). This suggests some type of overfitting.
I’ve been reading you occasionally for several months after having watched the Interstellar movie. So you suggest that a black hole is actually a tiny universe growing energy and strength to expand at some point?