Title: Resonant Removal of Exomoons During Planetary Migration
Authors: C. Spalding, K. Batygin, F. C. Adams
First Author’s Institution: Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA
Status: Accepted for publication in the Astrophysical Journal
We’re in the midst of a race to uncover planets of ever lower masses, planets orbiting at ever greater distances from their host stars, and yes—moons, their low mass companions. Will we find hordes of exomoons out there? Our first instinct is to cry yes—all the giant planets in our solar system have moons. Jupiter and Saturn each have at least 60 moons, Neptune has at least 14, and Uranus, 5. The acquisition of moons seems to be ubiquitous for our giant planetary siblings. But is it ubiquitous for giant planets beyond the solar system?
The authors of today’s paper take the bet and ask instead—having acquired moons, could the giant planets keep them? Giant planets are prone to wander, particularly in their infancy. This was one of the first of many surprising findings that the recent boom in exoplanet discoveries revealed. While in our familiar solar system, the gas and ice giants make their circuits furthest from the Sun among the planets, we’ve found hundreds of giant, Jupiter-like exoplanets extremely close to stars they orbit (thus their designation as hot Jupiters), all with orbits smaller than Mercury’s. There’s not much fodder for giant planet formation so near a star—only at distances such as Jupiter, which is 5 AU, or about fives times further from the Sun than the Earth, can you find enough material to form a giant planet. Therefore they must have roamed.
This journey might not be so friendly to the exomoons that call these roaming young planets home. The giant planets in our solar system have a hefty equatorial bulge, a byproduct of their fast rotation speeds and resulting centrifugal force—Jupiter’s polar radius is 6% shorter than its equatorial radius, and Saturn’s, the most oblate planet in the solar system, is 10% shorter (in comparison, Earth’s is only 0.3% or 13 miles shorter). This causes the orbits of their moons to precess—the plane of their orbits rotate, causing their point of closest approach to the planet to circumnavigate the planet, and the moons themselves to trace out rosettes around their host planets. Should giant exoplanets also be oblate, as our theories of planet formation predict, their moons should also precess.
A precessing orbit, though endlessly shifting, is stable. The trouble comes because there’s another source of perturbations that acts on a moon’s orbit: the host star. Such perturbations can also be periodic (with a period equal to the host planet’s orbital period) and stable, as it is for the Moon—in fact, the periodic irregularities seen in our Moon’s orbit due to the sun is called its “evection.” But when the periodicity of the moon’s precession and the star’s perturbations are similar, funny things can start to happen. The alignment of periods (or frequencies), also called a resonance, allows the host star to keep giving the moon a similar gravitational kick over and over again. These kicks add up coherently over many orbits, instead of adding randomly and canceling out as it would have otherwise, and cause the moon’s orbit to change drastically.
This “evection resonance,” as the authors call it, typically wouldn’t happen for the moons around a young giant planet that formed a few to tens of AU (the distance from the Earth to the sun) from its host star, as the moon’s precession period is much smaller than the period over which kicks due to the host star change. But when the host planet migrates towards its host star, this can change: inwards migration shortens the planet’s orbital period until it matches the precession period of its moon. Caught in resonance, the eccentricity of the moon can grow, bringing the moon closer and closer to its host planet every time it passes by. The moon can be forced onto such highly elliptical orbits that it collides with the planet and is destroyed (see Figures 1 and 2 below).
But the moon has chance to survive—if it can manage to escape the resonance early enough. The authors find that there are a couple of conditions under which the moon will not escape. Moons that have nearly circular orbits are more doomed than those with more elliptical orbits, as are those with orbits that are within about 10 times the radius of the planet. Those further than about 10x the radius of the planet could be locked into resonance, but the planet would stop migrating before the moon’s eccentricity would change its orbital path into one of collision.
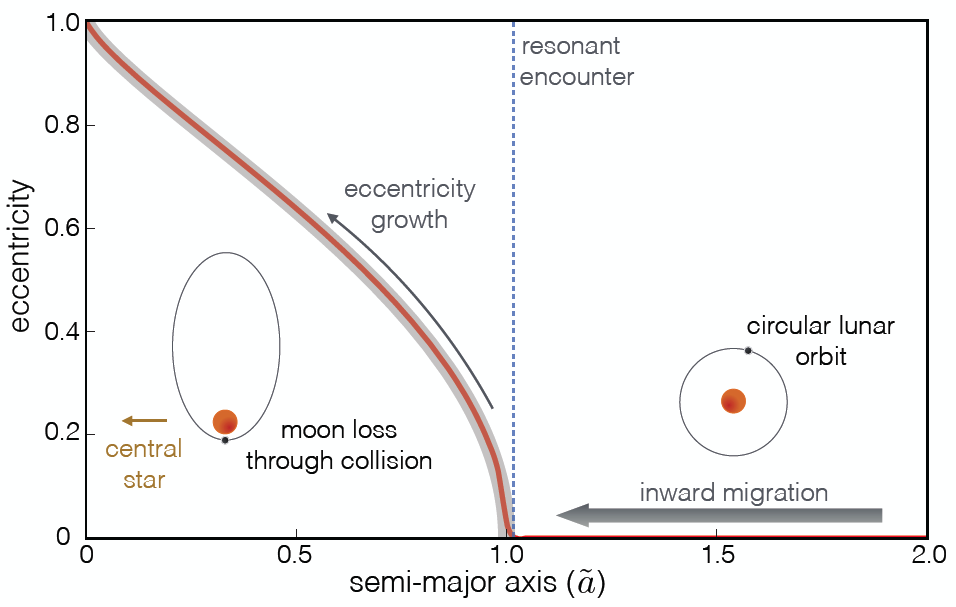
Figure 1. Cartoon of the growth of eccentricity of a moon’s orbit around its host planet after entering resonance. As a giant planet migrates inwards (moving leftward on this figure, which plots a normalized version of the planet’s orbital semi-major axis), a moon with an initially circular orbit (e = 0, also right inset) can be caught into a destructive “evection resonance” where the moon’s precession period equals its host planet’s orbital period (this occurs when the planet’s semi-major axis is about 1.0 in the normalized units here). The moon is forced into an increasingly eccentric orbit that could turn into a collision path with its host planet. Figure from today’s featured paper.
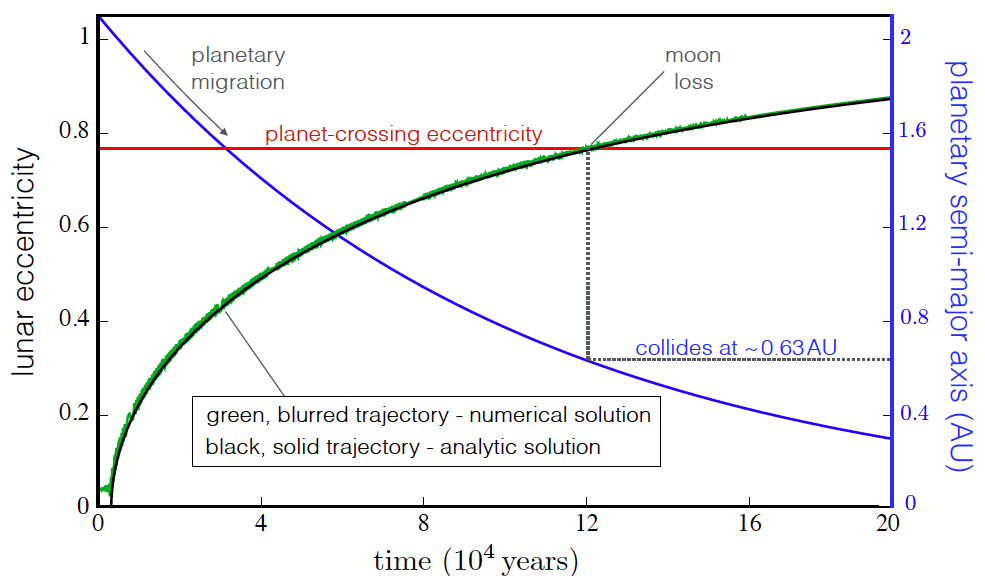
Figure 2. Death by collision with host planet. Plotted over time (in units of 10,000 years) in blue is a Jupiter-like giant planet’s inwards migration from 2 to a little under 0.4 AU. When the period of the planet’s orbit equals the precession period of one of its moons and is successfully caught in resonance (which here occurs shortly after t = 0), the eccentricity of the moon’s orbit grows (plotted both in green = numerical calculation and black = analytic prediction). The red line denotes the eccentricity at which the moon’s orbit would cause it to hit the planet. When the moon’s eccentricity crosses the red line (here at 120,000 years), the moon is destroyed. Figure from today’s featured paper.
As our telescopes and exomoon-finding methods improve, we’ll soon be able to tell whether the evection resonance plays a key role in the formation of moon systems around giant plants beyond our solar system. Stay tuned for more on exomoon discoveries!
Featured image from http://futurism.com/io-jupiters-moon/.