Today we have a guest post by Arazi Pinhas, a graduate student in astronomy at the Institute of Astronomy, Cambridge, UK. He researches theoretical aspects of exoplanetary astronomy.
Title: Curveballs in protoplanetary disks – the effect of the Magnus force on planet formation.
Authors: John Forbes
First Author’s Institution: University of California, Santa Cruz, Department of Astronomy and Astrophysics
Paper status: Published in MNRAS
Protoplanetary discs are the nurseries of planets. For planets to form the small dust grains in the protoplanetary discs must grow to planetesimals thousands of kilometers in size. Astrophysicists know how small grains and large objects can respectively combine through processes called collisional sticking and gravitational focusing. But there is currently no satisfactory bridge between these two size domains. This outstanding issue in the field of planetary formation is called the metre-sized barrier problem; in this size regime self-gravity is too feeble and collisional sticking too inefficient at creating bigger agglomerates. This problem was first discovered by Weidenschilling in 1977. His work showed that non-spinning bodies of approximately a metre in size drift into their host stars on timescales of about 100 years from 1 AU. This timescale is much too short compared to the typical lifetimes of protoplanetary discs, which are valued at a few million years. How then do bodies much larger than one metre evolve if their radial drifts are orders of magnitude smaller than protoplanetary disc lifetimes? This simple problem remains without a satisfactory answer to this day.
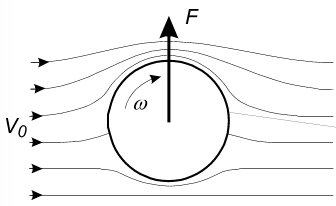
Figure 1: Schematic of the Magnus effect. The object has a leftward translational motion and clockwise rotation about its own axis. In the frame of the particle (which eliminates the translational motion) the ambient gas moves rightward with the same velocity, V0. This velocity field carves out a low pressure region on top and a high pressure region on the underside of the object. It is the pressure gradient which drives the object upward.
Magnus Effect
The paper investigates the Magnus effect to understand if it may be important in threading the two extremal sizes together. Figure 1 shows an illustration of the Magnus effect. A moving object spins clockwise with an angular velocity, Ω. In the reference frame of the object the ambient gas approaches it from the left with a uniform velocity V0. The Coanda effect describes the fluid moving over the top of the object: the fluid hugs the surface and rotates with the object. The underside is cleared of most high velocity particles, establishing a pressure gradient due to the Bernoulli principle. A force perpendicular to the vector of movement is induced. This force, F, is the Magnus force.
Disc Model with the Magnus Effect
Because the Magnus force arises for spinning objects it is naturally a function of angular velocity. To see the effect of the Magnus force on the motions of individual particles in a protoplanetary disc, the author of the paper integrates the equations of motion for the position, velocity, and spin of a particle in a gaseous disc. Figure 2 shows a sample result from this integration. We see that there is a visible difference of trajectories between a completely aligned particle (wz=1) and anti-aligned particle (wz=-1). We also see that the different spins can extend particle lifetimes by up to a factor of two, with a factor two increase occurring for a completely anti-aligned particle spin. Because the radial drift velocity is determined by wz, spin-aligned particles flow in fastest whilst anti-aligned particles flow in more slowly. This is consistent with simple considerations of a spinning object embedded in a fluid and acted upon by the Magnus force as we saw in Figure 1. The problem with this result is that though a completely anti-aligned particle with wz=-1 may achieve a lifetime twice greater than a spin-nought particle, the timescale is still comparatively small (negligible, even). There is no practical difference between a five-hundred year and three-hundred year lifetime when compared to the few million-year lifetimes of protoplanetary discs. In other words, inclusion of the Magnus effect in a gaseous disc does not alleviate the metre-sized problem.
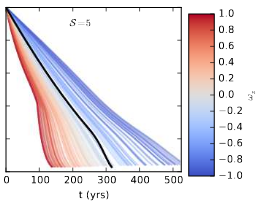
Figure 2: A color-contour plot of the projected angular velocity, wz, as a function of the semi-major axis and time for 100 particles with isotropically distributed spins over the sphere. An S of 5 means the spin rate, Ω, is relatively high. The color bar indicates how well the particle’s spin-axis is aligned with the disc’s angular momentum vector, with blue and red respectively representing anti-aligned and aligned particles. The black curve shows the case with zero spin for reference. The important message is that anti-aligned spins tend to increase the lifetime of a particle in the disk, as expected from consideration of Figure 1.
Implications for Theories of Planetary Formation
The Magnus effect might still offer definite implications for planetary formation scenarios. The paper first looks at a stability condition to suggest an answer. One conventional metric for the stability of a dust disc is the ratio of the vertical component of the host star’s gravity to the self-gravity of the dust disc. This ratio happens to be proportional to the velocity dispersion (i.e., a measurement of velocity spreads) of dust particles. For gravitational instability to occur, resulting in collapse of the dust to the mid-plane of the disc, this stability ratio should be about unity. Values too small or too large don’t allow for dust to collapse to the mid-plane of the disc. The value of this ratio is shown in Figure 3. The figure shows the ratio approaches nought at large distances from the star, where the Magnus force is generally weak. Nearer the star, large bodies are seen to have a comparatively large velocity dispersion; the stability ratio is high and runaway vertical gravitational collapse of the disc to the mid-plane does not proceed. But astronomers have indeed observed planets at such small radii from the star. What then are the logical consequences of these observations?
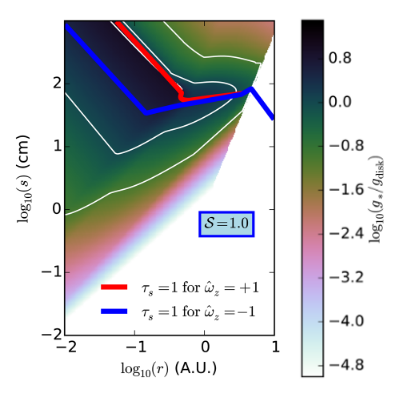
Figure 3: Color-contour illustration of the ratio gstar/gdisk, a stability criterion of a dusk disk against gravitational collapse. White contours show gstar/gdisk= 0.1, 1, 10. The conceptual message conveyed from this illustration is that the Magnus force alone is sufficiently able to arrest monolithic gravitational collapse for large bodies (greater than about 10 cm) at small distances from the star, thereby offering a few consequences for planetary formation models.
The paper offers three putative solutions. The first is that planets found at such small radii form at large distances and gradually migrate inwards. Another option is that planetesimals which interact gravitationally to form these planets themselves formed from dust grains smaller than about ten centimeters. Lastly, the author suggests that yet another means of concentrating particles, the streaming instability (see Youdin & Goodman’s 2005 work), may be at work. The author proposes that non-linear effects of this mechanism should be further explored because initially small rotation rates in the large-scale system may increase by the conservation of angular momentum during the material collapse to smaller system. This last suggestion, unlike the others, has not been well explored in the planetary formation literature. If fruitful, the Magnus force may play an interesting role in planetary formation.




Trackbacks/Pingbacks