Expected or not – It’s all the same physics

Title: Surprises in astrophysical gasdynamics

Authors: Steven A. Balbus & William J. Potter

Authors’ Institutions: Department of Physics, Astrophysics, University of Oxford; Laboratoire de Radioastronomie, École Normale Supérieure, Paris; Institut universitaire de France, Maison des Universités, Paris

Status: to appear in Rep. Prog. Phys

Why astrophysics is beautiful

A fascinating part of astrophysics is the following: regardless of the enormous range of scales occurring in astrophysics, the essential part of a phenomenon is often determined by one underlying fundamental process. Even more remarkable, such a key process can be an  analogue of a predominant process from a totally unrelated phenomena. That’s the beauty of doing physics – in the end it all comes down to a few fundamental equations.

Today’s Astrobite deals exactly with this underlying beauty, giving an overview of several fascinating astrophysical phenomena that can be explained with only four fundamental equations (namely the equations of magnetohydrodynamics MHD).

To quicken your appetite

The paper discusses many examples of idealized physical setups that may become unstable by changing one particular parameter. These instabilities can be expressed mathematically by solving the underlying equations analytically. Thinking through and solving the given examples provides a lot of deeper insight into processes that are important to be aware of in order to comprehend a more complex physical situation. However, our website is not called astrofeast, which is why this astrobite only consists of a brief heuristic description of two interesting, well-studied situations – evaporation in a cloudy medium and the magnetorotational instability. No equations occur in this astrobite, but to understand the underlying effects properly, you have to dig deeper into the maths.

Figure 1: An illustration of the setup in the first example. A spherical cloud of cold and dense gas evaporates with an expansion velocity into the hot and low-density surrounding due to the heat flux pointing towards the center of the cloud. [This figure is a slightly modified version of figure 1 in the featured articles.]

As a first example, the authors discuss the setup of a cool interstellar cloud, which they approximate with a spherical cloud filled with cold and dense gas in a hot medium of low density (figure 1). The pressure is approximately the same at all points in the cloud, and gravity is negligible. In such a scenario the outer part of the cloud will evaporate, and you might intuitively think that the mass loss rate is proportional to the surface area and thus to the square of the cloud’s radius. However, solving the problem properly reveals that the mass loss rate only scales with the radius and not with the square of it. The reason for this is astonishing: it turns out that the mass loss rate is proportional to the capacitance of the cloud, a quantity that otherwise occurs in the very different context of a conductor with zero surface potential and a given potential at infinity.

Magnetorotational instability

Probably the most actively investigated instability in astrophysics during the last 25 years – especially among researchers working with accretion disks – has been the magnetorotational instability, or in short the MRI. Interestingly enough, a specific case of the MRI had already been discovered by Velikhov in 1959 and independently by Chandrasekhar in 1960, but did not raise much attention before its rediscovery by Balbus (who is one of the authors of the featured paper) & Hawley in 1991.

One reason why the MRI has been studied intensively since then is the fact that it transports angular momentum radially outward and thus provides a possible solution to reduce the angular momentum in accretion disks around protostars and black holes. Regardless whether the MRI actually is the main contributor to angular momentum transport or not (recent studies indicate that magnetic braking is more likely the main mechanism for angular momentum transport around young protostars), the authors point out a very fascinating feature that magnetic fields can have: The MRI sets in as soon as a magnetic field is present, but neither its characteristics (instability criterion, maximum growth rate, most unstable displacement eigenvector) depend on any property of the magnetic field (neither the magnetic field’s shape nor its strength)!

That is why the MRI can be heuristically understood with the following analogy (figure 2): Imagine two point masses at two different orbits in a rotating disk that are connected with a spring (the spring acts as an analog for the magnetic field). Due to Kepler’s third law, we know that the inner point mass rotates faster than the outer one. Now, consider what will happen. The spring in between the two point masses is under tension and forces the inner point mass to move slower, while the outer point mass gets accelerated. But what happens next? The inner point mass that rotates slower than the Keplerian rotation, falls inwards and the outer point mass that moves faster than the Keplerian rotation moves outwards.

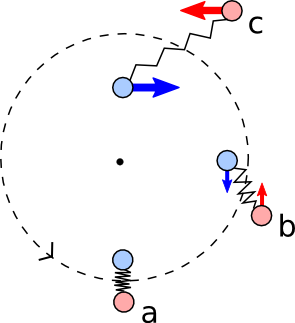
Figure 2: A schematic illustration of the magnetorotational instability. Two fluid elements are connected by a spring and due to this connection, the inner element transfers its angular momentum to the outer one causing the two moving apart from each other. [The figure is the same as figure on this website.]

Today’s Astrobite briefly presented two astrophysical phenomena that show remarkable physical analogs which are not immediately obvious, as well as non-obvious relations or properties. The article itself contains additional examples that are even more counter-intuitive, and provides useful references to very detailed studies of the presented phenomena. These results can also be understood as a warning, and might even be the biggest take-home message from the article. Intuition is important, but can be misleading. As shown in the article, it is crucial to carefully consider the validity and effects of a model’s assumptions before setting up your own model or before interpreting the results of others.

• About the Author

About Michael Küffmeier

I'm in the first year of my three-years PhD at the Niels Bohr Institute under the supervision of Åke Nordlund in Copenhagen. Besides fighting Scandinavia's bipolar disorder of darkness in winter time and overwhelming brightness in summer, I'm currently working on zoom-simulations. More precisely, on magnetohydrodynamic simulations of star and protoplanetary disk formation carried out with an adaptive-mesh refinement code called RAMSES. When I'm not in the office or traveling I'm probably somewhere else. If the weather allows it, I'm on the beach to improve my poor kite-surfing skills - with rather modest success.

Related posts:

Spinning the First Stars Small, but powerful Chondrules are old and everywhere – are solar system’s solid bodies built by them? How cold is Planet X?