TITLE: Orbital Stability of Multi-Planet Systems: Behavior at High Masses
AUTHORS: Sarah J. Morrison and Kaitlin M. Kratter
FIRST AUTHOR INSTITUTION: The University of Arizona, Tucson
STATUS: Accepted to ApJ
The Kepler satellite has ushered in an era of exoplanet research, with currently 1642 confirmed and ~3800 candidate planets (exoplanets.org). Do check out this awesome orrery of Kepler planets compiled by a professor at the University of Chicago. You’d probably be struck by the wide ranges of configuration, size, and number of the planets in these systems. Some revolve at breakneck speeds while others lazily plod along their orbits; some are baby planets while others are simply gargantuan in size. Within this colorful garden of exoplanet varieties, there emerges a common theme: a large fraction of these systems are multi-planet systems, not unlike our own Solar System. How stable are their orbits across a wide range of planet masses?
An orbit is considered stable if none of the bodies collide or are ejected after some arbitrarily large orbital periods. The dynamical stability has been studied extensively for low-mass planets, with planet-star mass ratio μ = Mplanet/Mstar < 10-3 (for example, the mass ratio of Jupiter with respect to our Sun is ~10-3). In low-mass multi-planet systems, stability is usually framed in the context of the Hill stability criterion, which gives the minimum orbital spacing to avoid collisions between any two planets. The critical radius is known as the Hill radius, measured in units of the mutual Hill radii of the two planets in this paper. The intra-spacing of planets is usually expressed in terms of the number of Hill Radius, or ΔHill. Direct orbital integrations with Np >= 5 low-mass systems show that the more widely-spaced planets are, the more stable the orbits become. Unlike low-mass systems, the orbital stability of massive multi-planet systems (or super-Jupiters, with μ >= 10-3) remains an open question. Does the low-mass stability trend extend to high-masses in the same manner? The authors seek to answer this question.
The authors ran a series of numerical integrations with various combinations of intra-planet spacing δ (a function of semi-major axes and μ; equation 3 in the paper), multiplicity Np, and planet-star mass ratio μ. They focused only on systems with Np=3 and Np=5 at μ = (10-5, 10-3, 10-2.5, 10-2); systems with more planets at the intra-planet spacings considered in this paper would imply formation in unphysically large and massive protoplanetary disks. Figure 1 shows instability time versus orbital spacing δ, as compared to lower-mass stability model shown as dashed lines. While high-mass planets also become increasingly stable at large planet-planet separations like their low-mass counterparts, the high-mass ratio and lower Np systems deviate somewhat from the low-mass relation. Given this, the authors explored if there is a different way to express planet-planet spacing that would result in an instability vs. spacing relation that is applicable across all mass ratios. The answer is yes, and for that one first needs to understand the source of instability within these systems: resonance overlapping.
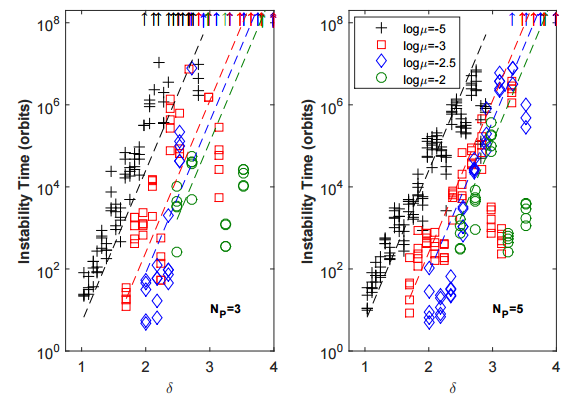
Fig 1 – Instability time in terms of number of orbits as a function of orbital spacing δ for Np=3 (left) and Np=5 (right) planet systems. The different markers refer to the different planet-star mass ratios μ while the dashed lines are relations from low-mass stability models. [Figure 2 of the paper]
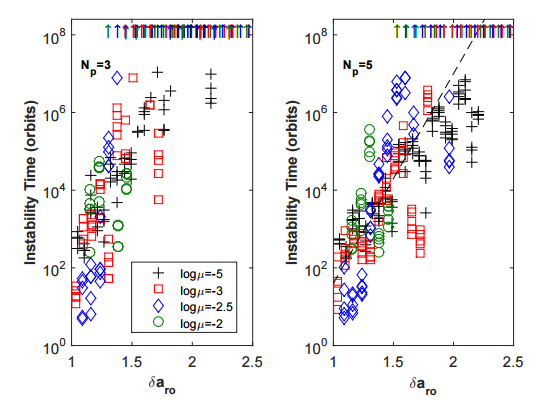
Fig 2 – Same as Fig 1 but now as a function of a new orbital spacing metric δaro, which is the fractional width of the zone where first order mean motion resonances overlap. [Figure 3 of the paper]