Title: Detecting gravitational-wave memory with LIGO: implications of GW150914
Authors: Paul Lasky, Eric Thrane, Yuri Levin, Jonathan Blackman, and Yanbei Chen
First Author’s Institution: Monash Centre for Astrophysics, School of Physics and Astronomy, Monash University, Australia
If memory serves…
Unless you’ve been living under a rock (or in a black hole) for the past few months, you should recall that the Advanced Laser Interferometer Gravitational-wave Observatory (aLIGO) recently announced the first direct detection of gravitational waves (GWs) by sensing ripples in the fabric of spacetime that emanated from the collision of two black holes, a signal dubbed GW150914. Following the announcement on February 11th, a profusion of papers have been published examining where such events originate, how the collision of two black holes can emit light, and so on. But today’s post covers a paper that you’ll be sure to never forget: the prospect of using aLIGO detections to uncover a strange effect called gravitational wave memory.
GWs have the effect of stretching and squeezing space, therefore altering the distance between objects. The amount of stretching and squeezing is quantified by strain, which is the change in distance between two points divided by the total (unperturbed) distance between two points. Strain scales with the strength of a GW, and to achieve the largest change in distance (which is essentially what LIGO measures), you want a large strain and a large distance between your two reference points. The main effect from a compact binary merger event (such as GW150914) is an oscillatory stretching and shrinking, with the magnitude of the strain increasing as the binary inspirals. The strain then goes back to zero after the GW passes through Earth (see the general shape of the figure below). However, if you look closely at the figure below, you may have noticed that the waveform shown in blue does not return exactly to zero. That is because this simulated waveform includes gravitational wave memory, a higher-order effect from general relativity that causes a permanent deformation between reference points.
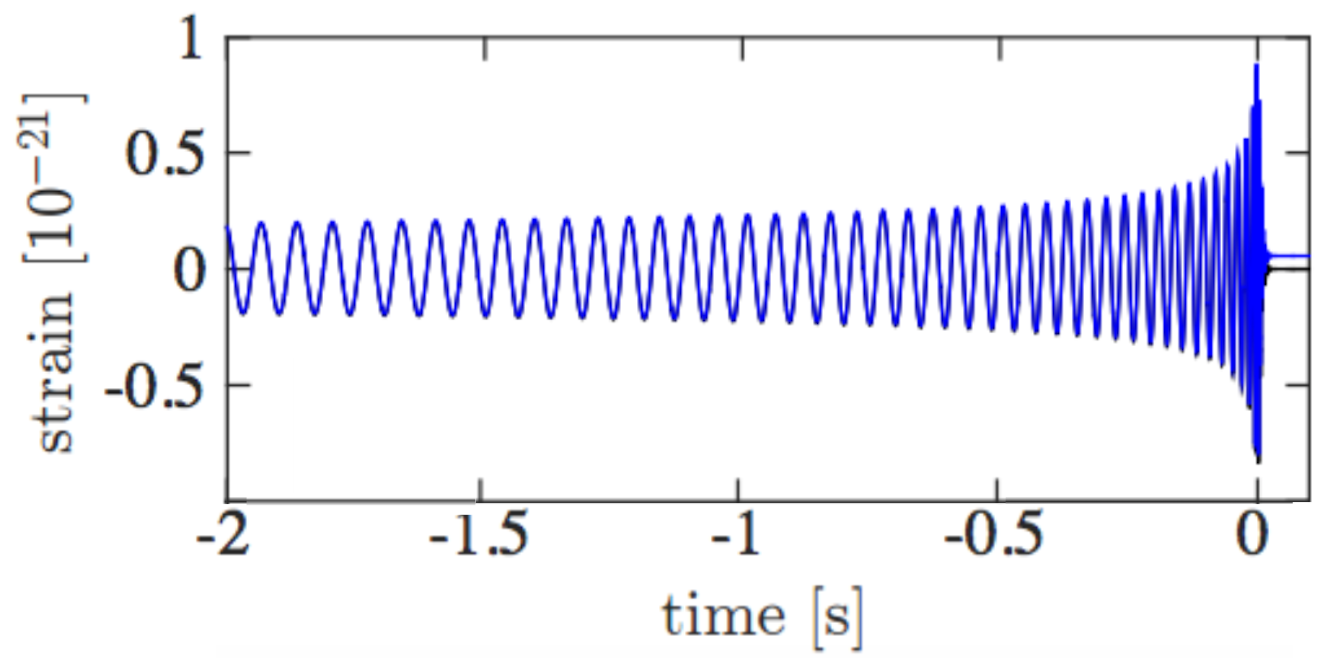
Simulated strain over time for a binary black hole inspiral with the parameters of GW150914, including the effect from gravitational wave memory. Though this includes the last 2 seconds of the binary’s evolution, GW150914 was only detectable by aLIGO for 0.2 seconds, or about 10 cycles. Adapted from figure 2 in today’s paper.
Similar to how light can have distinct polarizations (hence why polarizing sunglasses can reduce glare), GWs come in two different polarization flavors called plus and cross polarizations. To get technical, memory reveals itself in higher-order modes when one expands the polarizations of the strain in terms of spin-weighted spherical harmonics (check out this article if you want to dig into the nitty-gritty). However, the important things to know are:
- Memory induces a monotonically increasing (or decreasing) GW strain throughout the compact binary merger
- The memory component of a merger is about an order of magnitude smaller than the total strain for a merger
- Similar to the primary component of the GW strain, the memory component increases as the masses in the binary increase
- The memory component of the strain depends in the inclination of the binary (how the orbital plane of the binary is tilted relative to Earth), though it has a different dependence on inclination than the primary GW strain does
- To measure the sign of the memory (i.e. whether it caused a permanent stretch or shrink), one needs to accurately measure the polarization angle of a GW
The waiting game
Lasky et al. aim to predict whether aLIGO will be able to detect the effect of memory in GWs from compact binary mergers. For a single event, this effect would prove near impossible to detect. Taking an event like GW150914 as an example, at aLIGO’s design sensitivity the memory component would optimally provide a signal-to-noise ratio (S/N) of 0.42, whereas an S/N of about 3 would be the absolute minimum needed to possibly claim a detection. Instead, could we can wait for a very long time, building up this linear change in strain with each event until it is detectable? Not quite, since each event is equally likely to cause a permanent stretch or squeeze, and on average will cancel out.
The strategy that Lasky et al. take is to effectively “sum up” the low S/N contribution of many memory signals. With this approach it is necessary to know the sign of the memory for each individual detection (whether it caused a permanent stretch or shrink) so the effect of memory for each event will add coherently. As mentioned in the last bullet point above, this means that the building up of memory S/N requires GW events that have an accurately measured polarization angle.
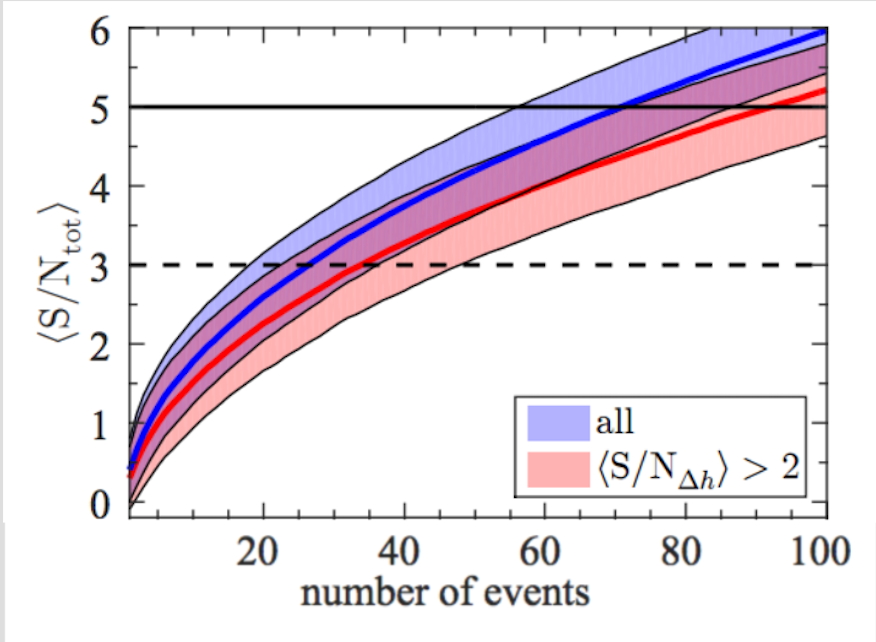
The buildup of GW memory S/N with the number of GW150914-like events. The blue line and shaded region represents the mean and error if all events are included, and the red line and shaded region represents the mean and error if only events with a measurable polarization angle (and therefore sign of the memory term) are included. The dashed and solid line represent a S/N of 3 and 5, respectively. Adapted from figure 3 in today’s paper.
In the limit that all mergers have the same S/N (i.e. each event is exactly like GW150914), the authors find that total S/N of the memory contribution scales as the square root of the number of events times the number of interferometers (currently, aLIGO consists of two interferometers in Hanford, WA and Livingston LA). The figure above shows the build-up of memory S/N with the number of detected events. Lasky et al. find that the cumulative memory of events will reach a detectable S/N of ~3 after the detection of ~35 GW150914-like events. Taking the aLIGO discovery paper for face value and assuming a GW150914-like event occurs every 16 days, this would indicate that GW memory would be detectable after only 1.5 years of aLIGO operating at design sensitivity!
I know what you’re thinking. Summer is around the corner, and many are still trying to shed that extra holiday weight and get their bodies in gear for the beach. Why don’t we just use gravitational wave memory to appear thinner without concerning ourselves with P90X and kale smoothies? Bad news: even if we orient ourselves in the correct way to align our stomach with the permanent shrinking of space from the memory of GW150914, our body would only shrink by about 10^-23 meters, about 100 million times smaller than the diameter of a proton. Plus, even if you had the best ruler in the universe, your ruler would shrink too. So now if you hear about rapid weight loss using gravitational wave memory on late-night television, you’ll know better.


Trackbacks/Pingbacks