Title: A periodic table for black hole orbits
Authors: Janna Levin and Gabe Perez-Giz
First Author’s Institution: Barnard College of Columbia University, New York
Status: Published in Phys. Rev. D, open access
Orbits around a black hole can be fascinatingly intricate. Surprisingly, the simple precessing ellipse we observe in planetary motion is not what we see close to a black hole. Rather these orbits exhibit something called “zoom-whirl” behaviour, tracing out patterns that look like four-leaf clovers. The authors concentrate especially on periodic orbits and catalogue these orbits into a “periodic table” according to their main features.
Anomalous precession of Mercury
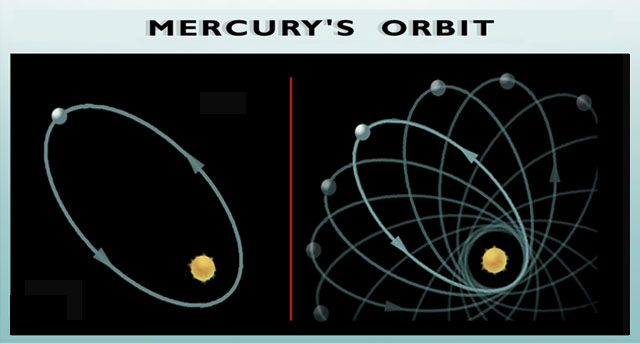
Figure 1: Left: Mercury’s elliptical orbit around the sun. Right: The long axis of the ellipse slowly rotates, i.e. precession of the perihelion. Source: http://archive.ncsa.illinois.edu/Cyberia/NumRel/Images/mercury.jpeg
For centuries, astronomers used Kepler’s equations to describe the orbital motion of all the planets—with the exception of Mercury. Mercury travels in an elliptical orbit, where the orientation of the long axis of the ellipse slowly rotates (i.e. precesses) around the Sun. This is referred to as the “precession of the perihelion of Mercury”, shown in Figure 1.
Newtonian physics does predict some precession of planetary orbits (for example, due to planets influencing each other’s orbits) but the predicted Newtonian precession does not match observations. Mercury’s peculiar behaviour remained a puzzle until Einstein’s Theory of General Relativity (GR).
Broadly speaking, GR is a theory of gravity that describes the way massive objects distort and bend the fabric of spacetime in their neighbourhood. The more massive the object, the more spacetime will be distorted by it, so relativistic effects are seen most strongly near very massive bodies such as stars and black holes. As the closest planet to the Sun, Mercury sits in a region of spacetime that is more distorted, leading to its more irregular orbit compared to the other planets.
Orbiting a black hole
The measurement of the precession of the perihelion of Mercury was a transformative moment for both Einstein and modern physics. However, Mercury’s orbit can be approximated by Keplerian physics even if the exact rate of precession is not accurate. This all changes where relativistic effects are very strong—near a black hole!
Let’s consider for a moment the motion around relativistic (i.e. extremely massive) objects such as a black hole. Imagine you are travelling in a space ship in the vicinity of a black hole. If you are far enough away, you will qualitatively orbit in pretty much the expected way: an ellipse. The fact that you are orbiting around a black hole in particular doesn’t really matter at this distance—black holes will act like any other spherical mass. Sure, the ellipse may precess, as discussed above, but nothing weirder than that.
As you move closer to the black hole, things start to get more interesting. The two radii we are concerned with here are the Innermost Stable Circular Orbit (ISCO) and the Innermost Bound Circular Orbit (IBCO). The IBCO is typically a smaller radius than the ISCO. Traversing the IBCO will generally lead to plunging orbits (unless you have a very powerful rocket to help you escape) that take you past the event horizon. The event horizon is the point-of-no-return; once you pass the event horizon of a black hole you cannot come back out! Outside of the ISCO, we see the familiar Mercury-type precession (the precessions of an ellipse) discussed above.
Zooming and whirling
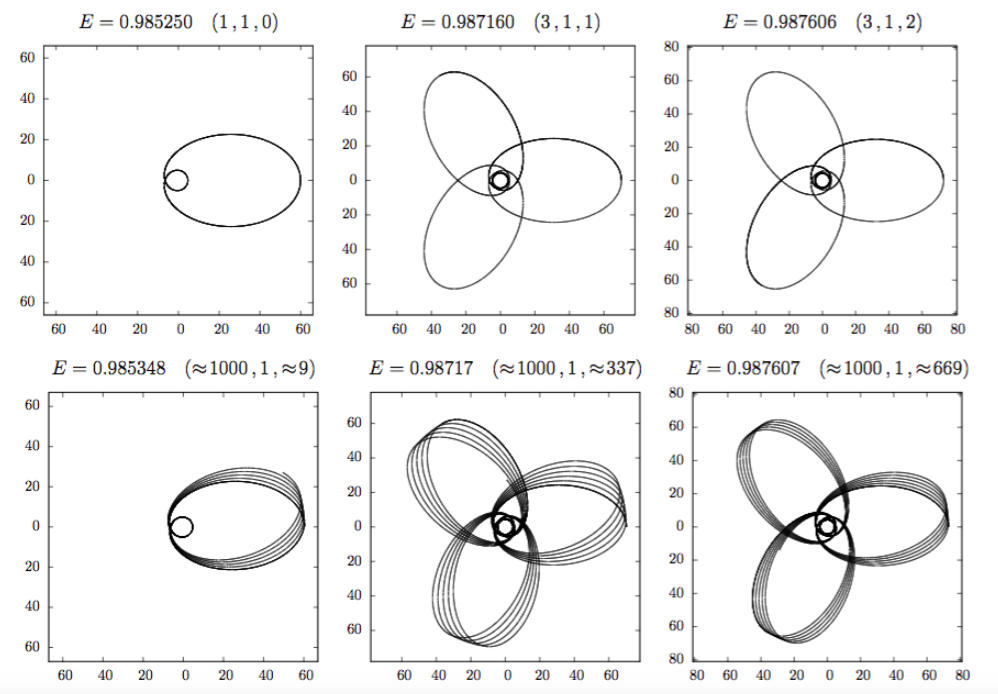
Figure 2: Examples of orbits traced out by a test particle around a black hole, where the black hole sits at the origin. Top row: Periodic orbits around a black hole. Bottom row: Nearby aperiodic orbits. Figure 1 in paper.
This paper focuses a lot on “zoom-whirl” behaviour, where you orbit the black hole in between the ISCO and IBCO. These complicated and intricate orbits look like patterns drawn with a spirograph (see Figure 2). A key feature of these orbits are the leaves (for example, you can trace out a four-leaf clover pattern as you orbit), which distinguishes them from Mercury-type orbits. Another interesting feature is that you can “whirl” around just outside of the IBCO essentially an unlimited number of times, and then “zoom” back out to trace along one of the leaves of the orbit. Zooms are the number of “leaves” of the orbits; whirls are number of revolutions around the IBCO before hopping back out.
An application of periodic orbits
Periodic orbits are special because they capture fundamental information about orbits around a black hole; all generic black hole orbits are small deviations from periodic orbits. We see examples of exactly periodic orbits and nearly periodic orbits in Figure 2. Cataloguing the periodic orbits in this way could lead to a powerful application: reducing the computational burden of gravitational wave calculations.
Gravitational waves (which are discussed extensively in this astrobite) are ripples in spacetime generated by massive objects interacting gravitationally. For example, two black holes spiralling into each other will generate a gravitational wave signal, which we can then observe using detectors on earth such as LIGO. The authors suggest that analysis using periodic orbits may yield computational advantages. For example, it may make signal extraction from time-frequency data an easier task.
Therefore, a periodic table of the weird and wonderful orbits around black holes is not just fundamentally fascinating, but may be useful for hunting gravitational waves.


Hello.The Quran(at-Tarik,1,2,3) writes black hole.
Gravity is a little big bigger than in Newton’s law; it increases with speed where the maximum is the double gravity in the case of light.
Global Physics also predicts the anomalous precession of Mercury’s orbit as Paul Gerber did 20 years before Einstein. http://www.molwick.com/en/gravitation/077-mercury-orbit.html