Title: Dynamical origin of extrasolar planet eccentricity distribution
Authors: Mario Jurić and Scott Tremaine
First author’s institution: Department of Astrophysical Sciences, Princeton University, USA
Status: Published in ApJ (2008) [open access]
If you fill your house with rocks and go away for a while, you may reasonably expect that the rocks will be there, in their original configuration, when you return. This is in the Constitution.
If you instead choose to decorate with lizards (which are bound not by the Constitution, but by lizard law), you will find your house much changed when you come back. No matter how you arranged them originally, several will have escaped, and the rest will be under your furniture (whence they will need to be chased if you want to salvage your decor).
Haters may say that planets are more like rocks than like lizards, which is true in the narrow sense that many planets are large rocks with gaseous envelopes, not reptiles with feet and external ears. But get a whole bunch of planets together, and they behave more like a house full of lizards than a house full of rocks. A system of planets placed in orbit around a star and left to its own gravitational devices doesn’t stick to its initial arrangement. Instead, the shapes of the orbits of the planets change over time. They grow more circular or more elongated as each planet feels the gravitational tug of other planets passing close by.
Curiously, when you average over many planets in many systems with many different initial orbital shapes, this gradual, chaotic, encounter-by-encounter change tends toward a particular final arrangement of orbital shapes, just as lizards tend to congregate under your couch with obnoxious disregard for their original placement.*
A suitcase full of planets
The authors begin by taking a supercomputer and dumping in a few thousand planetary systems. Each system consists of a central star and a handful of orbiting planets–sometimes as few as 3, or as many as 50. They give these planets a whole range of orbital shapes, or eccentricities: for some planets, circles, and for others, exaggerated, elongated ellipses. The orbit shape is determined by a parameter called eccentricity, or e, illustrated in Figure 1. e can range from 0 in the case of a circular orbit all the way up to very nearly 1 in the case of a long, narrow ellipse.
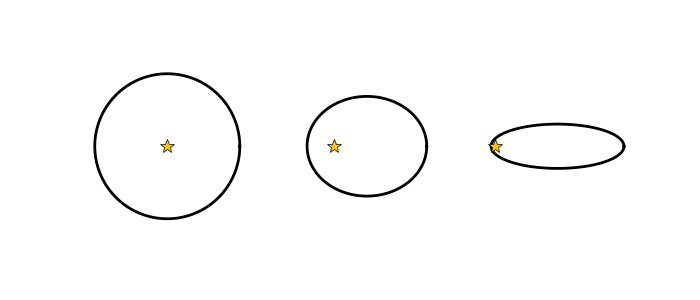
Figure 1: Three orbits around a star. From left to right, eccentricity e equals 0, 0.5, and 0.95.
They assign the eccentricities for each system according to a few slightly different rules: some systems have planets on circular orbits, while others have a mixture of shapes. (Crucially, they still love all the systems equally.)
Next, they let their simulated planets orbit, starting from these initial eccentricities, and watch their orbital characteristics change as time goes on. Early on, the systems are a bumper-car disaster of planet-planet and planet-star collisions, with a healthy additional fraction of planets fully ejected from their systems by close encounters (much like if someone in San Diego looked up and saw a few Disneyland bumper cars flying speedily southeast overhead). After a couple dozen million years, an average of only 2-3 planets per system remain, and after a hundred million years, their average orbital properties are stable.
A surprising convergence
After this evolution, about half of the systems (Figure 2, bottom panel, colored bands), despite their very different rules for initial eccentricity assignment, converge to astonishingly similar shapes.** These are the planetary equivalents of the under-couch lizards. Most of the remaining systems (Figure 2, middle panel, colored bands) appear to approach the same final state, but retain some imprint of their initial eccentricity distributions in the form of a low-eccentricity peak, which is like if you caught a couple of especially slow lizards in the act of moseying over to the couch from their initial perch on your shelf. Only one set of planets, which had completely circular initial orbits, is unchanged from its initial state, and this is the one that least matches a population of real exoplanets. It’s like it wasn’t even trying!
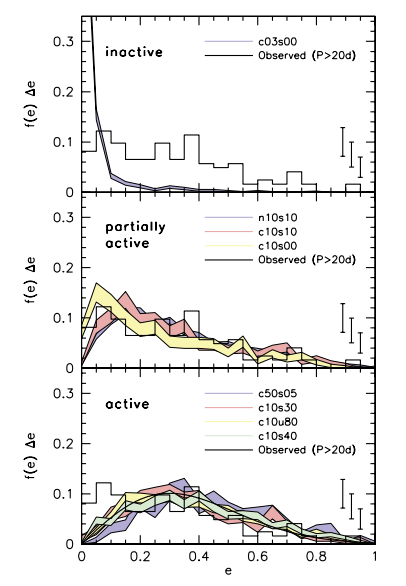
Figure 2: The final eccentricity distributions of the simulated planetary systems. Each colored band corresponds to a different rule for assigning initial eccentricities to planetary systems. One rule (that planets must start on circular orbits) yielded systems which hardly changed from the beginning of the simulation to the end (top panel); four others (bottom panel), despite their dramatically different initial conditions, converged on the same final eccentricity distribution, plotted as a smooth black line. The remaining rules (middle panel) appear to yield a mixture or superposition of the other types. The eccentricity distribution of real, observed exoplanets is plotted as a black histogram in each panel.
Why, and what next?
An underlying pattern emerges: the systems which converged to the same distribution in the end were tightly packed at the beginning, with little room (on average) between each planet and its nearest orbital neighbor. By the end of the hundred million years, enough of these uncomfortably close planets had collided with each other, been kicked out of their systems, or otherwise spread out that those that remained had some breathing room and no longer underwent frequent close encounters. In contrast, the few systems which maintained their initial eccentricity distribution throughout the simulation were adequately spaced out from the beginning. Our own solar system fits this bill, because the planets are adequately spaced out and all on quite circular orbits—making our solar system, yet again, a little bit different from the norm.
So what can we do with this information? For one, now that we know that planetary systems are likely to act this way, we can make smarter assumptions about planet populations in the future. And planet simulators can rest easier knowing that their choices of initial parameters don’t matter so much in the end, except for in systems like ours. Lizards, I suppose, can take this result as celestial validation and go about their decor-ruining business more smugly than ever.
*Please help me, my apartment is full of uncooperative lizards. I don’t want them to leave, I just need them to listen.
**After a hundred million years of evolution, lizards look less like this and more like this.
Featured image via Wikimedia Commons.

Nice one, Emily! Great to know if someone else who gets taken over by lizards.
The ones that my cat brought in and let go got into my clothes drawer and, err, pooped… Does that have a planetary system analogue??
Oh yes, the info about planetary systems was really interesting, too!
You say, “The authors begin by taking a supercomputer and dumping in a few thousand planetary systems”. Just like telescopes, if you reference a supercomputer or a group of supercomputers, you should credit them.
When reading the paper by Jurić and Tremaine, I couldn’t see that they themselves named the computing facility they used. All I could see relating to this was,
“This research was supported in part by NASA grants NNG04H44g and NNX08AH83G, and used computational facilities supported by NSF grant AST-0216105.”