Title: Breaking the Chains: Hot Super-Earth systems from migration and disruption of compact resonant chains
Authors: Andre Izidoro, Masahiro Ogihara, Sean N. Raymond, Alessandro Morbidelli, Arnaud Pierens, Bertram Bitsch, Christophe Cossou, Franck Hersant
First Author’s Institution: Laboratoire d’astrophysique de Bordeaux, University of Bordeaux
Status: Submitted to MNRAS [open access]
To migrate, or not to migrate? That is the question. Of course, since planets are not Shakespearean characters, they should not have a choice! When a planet forms in a disk, it creates two spiral waves: a weaker one ahead of the planet that drags it forward (sending the planet outwards), and a stronger one behind the planet that pulls it backwards (sending the planet inwards). Ultimately, every planet should migrate inwards and in most cases, end up much closer to its star than where it formed.
When planets in the outer disk migrate inwards faster than planets closer in, they start to catch up to each other. As these planets get closer together, they eventually become gravitationally locked into resonance: pairs of orbits where the outer planet takes exactly twice as long (or another integer ratio such as 3-to-2, etc.) to complete an orbit around its star as the inner one. Once this happens, the planets migrate together, maintaining that 2-to-1 ratio. In systems with many rocky planets, the third one will follow suit and fall into a resonance with the second planet, as will the fourth with the third, and so on. Eventually, the system will have a long chain of up to 10 resonant rocky planets tightly packed in the inner part of the disk!
Yet even though migration is supposed to be inevitable, only about 5% of the planetary systems discovered by the Kepler mission are actually in this setup (TRAPPIST-1 is the most famous). The other 95% are not, many of which because they only have one planet. Today’s paper, led by Andre Izidoro, attempts to explain these discrepancies by suggesting that all systems migrate into resonant chains, but not all of them stay in resonant chains!
Two-Phase Setup
Izidoro et al. study this problem by conducting two-phase N-body simulations of 120 hypothetical planetary systems with 20 to 30 rocky planets for 100 Myr. These planets start out with 0.1 to 4.5 Earth masses and are spread out evenly in the outer disk beyond 5 AU.
- In phase one (0 to 5 Myr), the planets may migrate due to the presence of a gaseous protoplanetary disk. Meanwhile, the disk also keeps the planets on flat, circular orbits by damping the planets’ eccentricities and inclinations.
- In phase two (5 to 100 Myr), the planets can no longer migrate since the disk has dissipated away. However, they are free to develop eccentric and inclined orbits since they are now controlled by interactions with each other instead of interactions with the disk.
Compact, but not too compact
Izidoro et al. find that all of their planetary systems migrate into compact resonant chains within 1.5 Myr, safely less than the disk’s lifetime of 5 Myr. Many of these systems (40%) then survive as resonant chains for the entire 100 Myr simulation.
However, some systems (60%) become too compact (see Figure 1). In particular, the ones that are too compact with higher mass planets become unstable after the disk fades away! The resonant chains then collapse as some of the planets eject and the rest spread farther apart. As they spread out, the surviving planets’ orbits also become more eccentric and inclined.
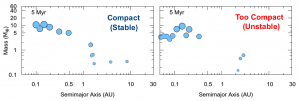
Figure 1. Two example resonant chains after phase one. The first system (left) will survive phase two (without the disk). The second system (right) will become unstable because it has more planets too close together. Some of the surviving planets will develop inclined orbits, making them less likely to transit. Adapted from Figs. 2 and 3 of the paper.
Single-Planet Imposters
In order to compare their results with actual exoplanet systems discovered by the Kepler Mission, Izidoro et al. must determine what fraction of their planets can transit (and be “detected” by Kepler). They find that in the stable resonant chains, Kepler can detect 3 or more planets in 66% of these systems. On the other side in the unstable systems, the inclined orbits from the instabilities make it so that Kepler can only detect 1 planet in 78% of these systems, even though over 90% of the unstable systems still have multiple planets.
Explaining the Kepler Dichotomy
One of the defining features of Kepler’s planets is the large number of systems with only one transiting planet. Naturally, we expected that Kepler would not be able to find all of the planets in each of its systems since planets at large separations from their star that do not line up with our line-of-sight will not transit. However even with this bias, the fact that there are so many more single-planet systems than two-planet systems (see Figure 2) suggests that Kepler systems belong to a dichotomy: roughly 50% of all systems have just one planet (including non-transiting ones) and 50% have many planets (5+ for small stars). Such a high fraction of single-planet systems is a huge surprise, given how many planets exist in our own solar system.
However, the two populations of planetary systems in this study offer an explanation for the Kepler dichotomy that would imply these single planets are not so lonely. Izidoro et al. calculate that if no more than 25% of all planetary systems are compact resonant chains (with the rest being unstable systems), this distribution of systems can match the high fraction of systems with just one transiting planet in the Kepler dichotomy — even though nearly all of these systems would have multiple planets.
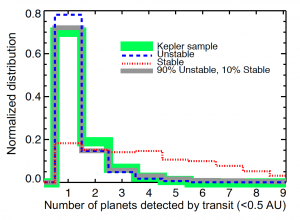
Figure 2. Comparison of Kepler’s planetary systems to this paper’s planetary systems. In the Kepler sample (green), the vast majority of systems have only one transiting planet. The unstable systems in this paper (blue) would have even more single-transit systems, while the stable resonant chains (red) have a lot fewer. A proper balance between these two (90% unstable, 10% stable — gray) matches the Kepler dichotomy pretty well. Fig. 15 of the paper.
Why so unstable?
Izidoro et al. expect that in reality, roughly 5% of all planetary systems are stable resonant chains (since this is the fraction found by Kepler), which is consistent with their upper limit of 25% they need to explain the dichotomy. Even though the authors find that 40% remain stable in their study, they suspect that simulations with a more realistic protoplanetary disk would lead to many more systems going unstable. Nonetheless, the authors caution that their model remains incomplete until they find a reason for ~95% of Kepler’s systems becoming unstable at some point in their history.
It may also be the case that not all systems migrate into resonant chains to begin with, or even that planets do not migrate as easily as this study presumes. For now, we can still take solace in knowing that at least some of Kepler’s single-planet systems have non-transiting companions that they can orbit with for billions of years.
Featured Image Credit: 3rd-author Sean Raymond (Check out his summary of this work here.)


Trackbacks/Pingbacks