Title: Bayesian evidence for the prevalence of waterworlds
Author: Fergus Simpson
First Author’s Institution: University of Barcelona
Status: Published in MNRAS, open access
We exist.
That might seem like an obvious statement, but it’s one of the observations that drives today’s paper.
It’s a provocative piece of work by Fergus Simpson, which attempts to understand – robustly and with Bayesian statistics – what we can infer about potential aliens based on the data point that is us. Given that we exist, and our planet is like this, can we infer anything about other planets that host intelligent life? This Bayes primer might be useful if you’re not familiar with the concept.
Simpson is responsible for the Big Alien Theory, where he predicts that aliens typically live on planets smaller than Earth and weigh around 300kg. For more on that, see the paper and his website explaining the idea.
This is a follow-up to that paper, with a focus on the water coverage of planets that host intelligent life.
Simpson first points out that the Earth is very finely water/land balanced: the surface has almost equal quantities of each exposed. Is there feedback that drives habitable zone planets towards being near this balance, or did we just get lucky? Although several possible methods for feedback are discussed in the paper, none seem powerful enough to make the majority of habitable zone planets have such a close balance of surface water and surface land.
Balanced planets seem like a good place for life: if there is very little water, most land become an arid desert, unable to support life. If a plant is entirely covered in water, there can be no land-based observers. The more non-desert land a planet has, the easier it is to evolve, and the more life there is. Simpson only addresses land-based observers – see the end of the article for details.
The paper looks specifically at the basin saturation. This is defined as the ratio between the volume of surface water and the volume of liquid required to cover half the surface of the planet. This gives us an understanding of how much of the planet is covered in ocean.
We can approximate the volume of surface water (water not tied up in the core of the planet) by multiplying four quantities:
- The water mass fraction of the planet, for which previously published simulations are used.
- The total mass of observed planets: to calculate this, Kepler data on occurrence of planets by radius and an experimentally-determined mass/radius relationship are used.
- The fraction of total water that sits at the surface. This is assumed constant, and any variation is absorbed into the variation in water mass fraction.
- The inverse of the water density, to convert mass into volume.
We can then calculate the volume of liquid required to cover half the surface of the planet based on the surface area of the planet and the elevation profile across the surface. Combining these gives an expression for the basin saturation.
Simpson finds that our best understanding of these various quantities suggests that there should be quite a lot of variation in basin saturation between planets. He can use this fact to draw two conclusions.
1: We’re special
The high level of variation in basin saturation suggests that most habitable zone planets are highly polarised: they are either arid deserts, or ocean-dominated waterworlds, as demonstrated in Figure 1.
Let’s make two assumptions. Firstly, the habitable land area is maximised if there’s a good water/land balance, which avoids the planet being dominated by either desert or ocean. Secondly, the greater the habitable area, the greater the number of observers. So most observers exist on planets with high habitable land area, and as such a fairly close balance of surface water and land. The distribution of ocean surface fraction, weighted by observers, is shown in the right of Figure 1. An observer is significantly more likely to observe their own planet being Earth-like, than to observe a random habitable zone planet being Earth-like, in terms of surface water. We’re not here on Earth just because Earth is habitable zone, we’re here because Earth has the right quantity of surface water for intelligent life to happen. As the paper states, “The Bayesian evidence for anthropic selection is substantial”. And planets with Earth-like surface water coverage are more likely to host life than random habitable zone planets.
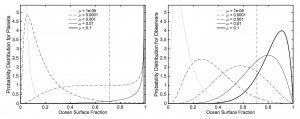
Figure 1. Left: The distribution of planets by ocean surface fraction, as a function of μ, the median water mass fraction. The higher the curve, the more planets there are with that water mass fraction. Most guess for μ lead to either a majority of desert planets or a majority of waterworlds, and μ has to be carefully tuned for Earth to be ‘normal’. Right: The distribution of observers by ocean surface fraction (see text for an explanation) is much more favoured towards Earth. Figure 4 in the paper.
2: Water, water, everywhere!
Bayes theorem states that:
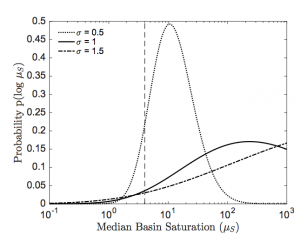
Figure 2: The expected median basin saturation for habitable planets. σ represents the variation of basin saturation between planets: in the paper this is calculated to be ~1, but the qualitative results don’t change much with value: most habitable planets are heavily water-dominated. Figure 5 (left) in the paper.
In this case, we’d like to infer the expected distribution of median basin saturation (which roughly means the average amount of water on a planet), based on our observation that Earth has a basin saturation value around 4. We’ll do this based on the likelihood of selecting the Earth from underlying distributions with a range of median basin saturations, and a prior expectation of median basin saturations. Simpson uses an uninformative prior in log space, meaning he assumes that every magnitude of median basin saturation value is equally likely. More on that in the health warning at the end of this, but he’s trying to avoid this choice of prior influencing the outcome. The posterior, i.e. the likelihood of each different median basin saturation value, is shown in Figure 2.
That was a mouthful! Basically, Figure 2 shows Simpson’s calculation of how likely planets are to be water covered. A higher probability means the associated median basin saturation value is more likely, a higher median basin saturation means more surface water on most planets. The three models (solid, dashed and dotted lines) represent three different guesses for the variability of basin saturation between planets. In all cases, Earth is unusually dry for a habitable zone planet, and we expect most habitable zone planets to be waterworlds.
Now, we expect that near-future missions (JWST, WFIRST, the E-ELT and the TMT to name a few) will reveal a lot more about the surfaces of habitable planets. These new data points will help to refine the ideas above, and allow us to update our understanding of the conditions needed to evolve intelligent life. Any biases, towards or away from Earth, will help us to understand why we evolved here on this particular piece of rock.
Health Warning
This next section comes from my brain, rather than from the paper. But I think it’s important that we present this in parallel with the paper. Bayes’ theory is a really interesting statistical tool, when used properly. But it’s worth discussing whether Simpson’s analysis is valid, and whether the underlying assumptions are correct. Points to note are:
- All priors inherently carry some information: no prior is entirely uninformative. It is worth asking whether the form of the prior influences the broad conclusions of this paper, and whether uniform in log space is a fair choice.
- The calculation that there is significant variance between planets in basin saturation is key to this analysis. If new evidence arises that suggests the variance is actually low, the conclusions change.
- Simpson considers only land-based observers. The logic behind this is that we are land-based, and therefore land-based observers are more likely. I worry, albeit without rigorous maths, that if waterworlds are very common then that conclusion itself amplifies the likelihood of water-based observers. Intuitively it feels contradictory, but as we know statistics often isn’t contradictory.
- If, as in the paper, one states most planets are water dominated (>90% surface water) at a 95% credible interval, this means that 95 out of 100 random observers – random humans or aliens on their various planets, can make observations of their own planet, follow the logic presented in their paper, draw a similar conclusion, and be correct. It is of course perfectly possible that Simpson is one of the 5 random observers that is incorrect.
My recommendation is to take this paper as an interesting statistical idea and a starting point for discussions, and not as the be-all and end-all for extra-terrestrial life.