Title: Advection of potential temperature in the atmosphere of irradiated exoplanets: a robust mechanism to explain radius inflation
Authors: P. Tremblin, G. Chabrier, N. J. Mayne, D. S. Amundsen, I. Baraffe, F. Debras, B. Drummond, J. Manners, S. Fromang
First Author’s Institutions: Maison de la Simulation, CEA-CNRS-UPS-UVSQ, USR 3441, CEA Paris-Saclay
Status: Accepted in ApJ [open access]
In the field of exoplanets, hot Jupiters are the first friends we discovered two decades ago. We now know they are usually loners. They are most likely not formed in situ but migrated from the outer disk. They are expected to be synchronized to their parent stars by close-in tidal interactions. Nevertheless, there are still a few open questions that we do not understand yet. The inflated radius is one of them (see this previous bites). In today’s paper, the authors provide a new approach to tackle the conundrum.
Puffier than they ought to be
Hot Jupiters passively cool down and contract after formation. Standard models can predict their thermal history and how much their radii should contract up to present time. Yet the observed radii (e.g. through transit) are larger than prediction. It is more surprising if you realize that it is difficult to increase the size of these gas giants. Because they are supported by pressure from electron degeneracy, it works in a way that the size remains almost constant with increasing mass. The possible solutions to this problem can basically be categorized into two types: (I) constantly injecting energy into the interior (II) delay the cooling process. (I) includes downward transport of kinetic energy, or energy dissipated by the interaction with the magnetic field (ohmic dissipation). Enhanced opacities are also proposed to reduces the cooling rate, which belongs to (II). However, the above mechanisms are either not robust or restricted to fine-tuned parameters. So the radius anomaly remains an intriguing open problem.
The power and the limit of the 3D GCM
A lot of effort have been put into 3D general circulation models (GCM), which solve a full set of equations describing the motion and energy of the fluid. They are the most sophisticated models to study flows in the atmosphere and also computationally expensive. So far none of their results can provide the mechanism responsible for the inflated radii. It is either that we are missing fundamental physics in these models, or as the authors argue, these models simply don’t run long enough to reach a steady state in the deep atmosphere, where the thermal inertia is too large (the timescale of thermal radiation is proportional to pressure). To overcome this problem, they developed a steady state solution to obtain the converged temperature structure that is prohibited by the 3D GCMs.
2D steady state model
To simplify the problem and to look for the steady state, the authors drop all the temporal terms and only consider the solution at the equator. After massaging the equations, they obtain a reduced system, which looks less daunting but is underdetermined, i.e. there are an infinite number of solutions would satisfy the equations. They play a trick by imposing inputs from the 3D GCM to constrain the system: one is the zonal wind profile at the substellar point, and the other provides the overall geometry of the wind. Including these two conditions, together with proper boundary conditions, the 2D steady solutions describing the flow at the equator can then be solved.
The comparison between the 2D solutions and 3D runs is shown in Figure 1. The day-night temperature profiles and the global structure of the wind are mostly well reproduced by the 2D solutions. The main difference is the pressure-temperature structure of the deep atmosphere. The 2D solution converges to a hotter adiabatic profile required for a larger radius. On the other hand, the 3D model still tries to heat the deep atmosphere, leading to the artificial high vertical velocities seen in the bottom panel. Although the vertical velocities below 1 bar in the 2D solution are small, they are not zero. Since the deep atmosphere has a high density, the vertical mass fluxes are significant enough to drive the downward transport of entropy. This causes the temperature to connect to the hotter interior, even in the absence of convection. Similar processes are also found in the Earth deep ocean. So coming from simple equations, this adiabatic adjustment naturally solves the radius inflation problem!
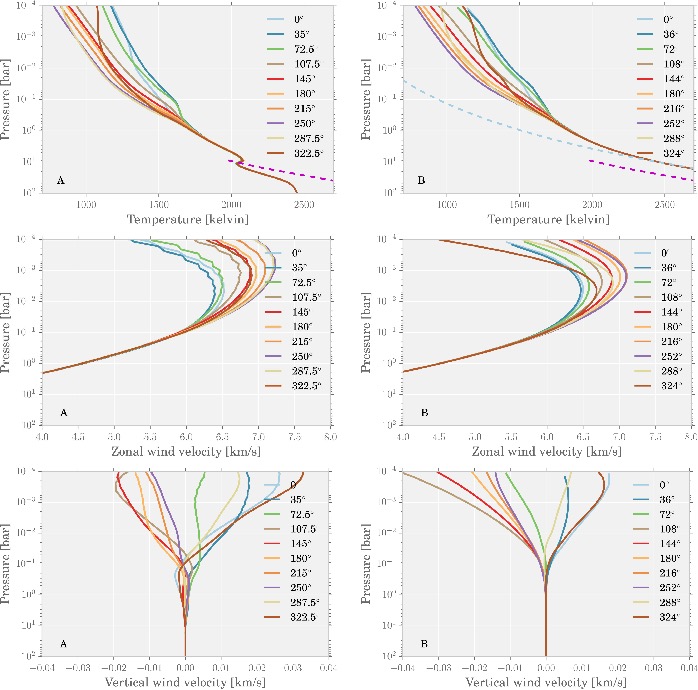
Figure 1: (From top to bottom) Temperature, zonal wind, and vertical wind profiles for different longitudes shown in different colors. A (left) is from the 3D GCM run and B (right) is from the 2D steady state model. The pink and cyan lines are adiabatic thermal profiles corresponding to 1.4 RJup and 1.6 RJup respectively from the evolutionary model. (Figure 2 of the paper)
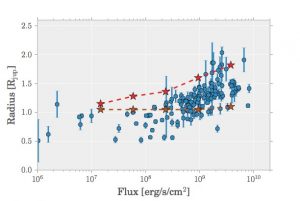
Figure 2: Correlation between irradiation flux and inflated radii. The red is from the 2D steady solutions and the brown is from the 1D models, compared with observation points (blue) from www.exoplanet.eu (Figure 6 in the paper)
Even puffier when closer to the stars
People have also found the correlation exists between observed inflated radii with increasing stellar flux, as displayed in Figure 2. The proposed theory, if were universal, should be able to show the dependence of stellar irradiation. Their 2D models (red), based on the same physical set up, do successfully produce the trend of increasing radii with increasing irradiation without parameter-tuning. Thus it provides a robust mechanism solving the radius inflation problem. The steady-state model can be a useful tool to understand the long-term process in the atmospheres. The authors demonstrate how it provides a new way to solve the long-standing puzzle of inflated radii. I am excited to see more studies applying a similar approach to different problems.



Trackbacks/Pingbacks