- Title: A Paucity of Proto-Hot Jupiters on Super-Eccentric Orbits
- Authors: Rebekah I. Dawson, Ruth A. Murray-Clay, John Asher Johnson
- First Author’s Institution: Harvard-Smithsonian Center for Astrophysics
Note: This post is based in part on a talk by Rebekah Dawson at the UC Berkeley Planet and Star Formation Seminar on Nov. 7, 2012.
Introduction
How do planets form, and after formation, how do they change their orbits (or “migrate”) to come to their present orbits? The increasing catalog of confirmed exoplanets (planets around other stars), in tandem with the also increasing list of exoplanet candidates discovered by the Kepler Mission, is making it possible to answer these questions through statistical tests of the exoplanet population.
The authors investigate the formation history of a particular population of exoplanets called hot Jupiters, Jupiter-size planets in short orbits (in this study, 3-10 days) around their stars. The consensus among most scientists is that hot Jupiters are too big to have formed in their present location; they more likely formed oustide the “ice line,” or the radius at which water can freeze. This is because frozen water molecules can clump into tiny ice crystals, which could then aggregate into larger snowballs to form giant planets. Very few proposed mechanisms (such as core collapse, in which a clump of gas spontaneously collapses to form a planet) could form Jupiters inside the ice line, and these mechanisms are disfavored based on the current body of observations. Thus, theory says that hot Jupiters should have formed beyond the ice line and then migrated inward to their current, super-hot abodes. But how did they get there?
There are two popular theories that could bring a Jupiter from beyond the ice line to a hellishly hot orbit. One is “disk migration,” in which friction between the newly formed Jupiter and the protoplanetary disk from which it formed slows the Jupiter, sending it spiraling inward. The other is “high-eccentricity migration,” in which another massive body in the system–either a companion star or another planet–kicks the Jupiter into a high eccentricity orbit through gravitational interaction. If the closest approach of the planet to the star (periapsis) is sufficiently close, tidal forces from the star convert the planet’s orbital energy into heat, which causes the orbit to circularize, over many many orbits, at periapsis. The authors call Jupiter-size planets that are in sufficiently high eccentricity orbits to eventually tidally circularize (e > 0.9) “super-eccentric,” whereas planets with 0.6 < e < 0.9 are “highly-eccentric” and those with 0.2 < e < 0.6 are “moderately-eccentric.”
A former paper by Socrates et al. (2012) predicts that the Kepler planet candidates should include 5-7 super-eccentric Jupiters. Dawson et al. (2012) test this by measuring the eccentricities of Jupiter-size candidates in long orbital periods. The authors find zero super-eccentric Jupiters among the Kepler planet candidates, as compared to the 5-7 expected from high-eccentricity migration.
Method
How do you measure the eccentricity of a planet? Historically, the eccentricities of planets have been measured via the radial velocity method, which monitors the motion of the star toward and away from the observer to infer the presence of the planet and the planet’s mass as the planet and star orbit the system’s center of mass. Deviations from a sinusoidal variation in the radial velocity of the star indicate the eccentricity of a the planet. However, most Kepler stars are too faint for even the most powerful instruments to measure their radial velocities. The authors’ solution was to derive the planet’s eccentricity from the Kepler light curve.
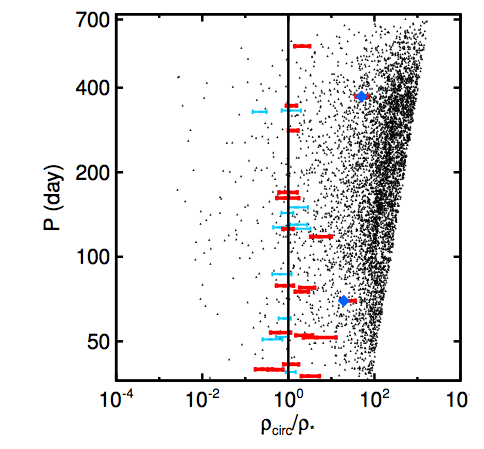
Figure 1. Period and ρcirc/ρstar measured from the Monte Carlo simulated data (black points) and the Kepler light curves of long-period Jupiters (colored bars). Light blue bars are Jupiters that have companion planets in their system; red bars are Jupiters with no detected companions. The two blue diamonds indicate highly- (but not super-) eccentric Jupiters. From Dawson et al. (2012).
The authors measure the eccentricity from the duration of the planet transit compared to the depth of the transit. To recap for those who are unfamiliar: a transit occurs when the planet passes between its star and the observer, dimming the star’s light temporarily. Since the fraction of the starlight blocked during a transit is proportional to the area of the surface of the star that is blocked, the depth of the transit is proportional to the radius of the planet over the radius of the star squared. The duration of the transit depends on the radius of the star, the impact parameter (the minimum projected distance between the planet and the star) the orbital distance of the planet, and the planet’s speed at that point in its orbit–which depends on the star’s mass and the eccentricity of the planet’s orbit! So, as you might have guessed, the eccentricity could be confused with other parameters when determining the eccentricity from the light curve alone. The major competing parameter is the stellar density, ρ. The authors get around this parameter degeneracy by comparing the calculated density ρcirc to a more reasonable estimate of the stellar density from observational parameters, ρstar. The ratio between these calculated densities is a proxy for the planet’s eccentricity.
To test the validity of their method, the authors tried it on a planet with a large, known eccentricity (as determined by the radial velocity method). Their method reproduced the radial velocity-determined eccentricities very well, with a slight systematic overestimate of eccentricity. Therefore, this method should not miss the super-eccentric Jupiters.
To figure out how many super-eccentric Jupiters they expected to find, the authors assumed a constant “current” of hot Jupiter formation, meaning that there should be Jupiters at super and moderate eccentricities at all times. They used the number or observed hot Jupiters (Jupiters in circularized orbits between 3 and 10 days) and moderate-eccentricity Jupiters in the Kepler data to produce a Monte Carlo simulation of super-eccentric hot Jupiters they expected to find in the Kepler data. They then calculated the expected distribution in ρcirc/ρstar. Within the Kepler data, the authors selected planets larger than 8 Earth radii, in periods of at least 36 days, and around host stars with temperatures between 4500 and 6500 K and surface gravities larger than log(g) =4, where g is the gravitational acceleration at the star’s surface. The planetary criteria select Jupiter-size planets that are far enough away from their stars to still have eccentric orbits; the stellar criteria select the best-characterized subset of the Kepler data, for which the errors in stellar and planetary parameters are small. The Monte Carlo simulated data and the selected data from the Kepler light curves are shown in Figure 1.
Result and Significance
Dawson et al. find zero planets in the super-eccentric regime, as compared to the 5-7 they predicted (see Figure 1). The result of no super-eccentric Jupiters in the Kepler data rules out the expected range of 5-7 with 98.7% confidence (a confidence larger than Nate Silver‘s confidence in Obama’s victory in last week’s presidential election). This result suggests that high-eccentricity migration (HEM) is probably not the dominant channel for hot Jupiter formation, and that disk migration or a variation on HEM processes involving Jupiters that are formed or kicked to within the ice line produces the observed population of hot Jupiters. However, HEM could still account for a fraction of the hot Jupiters (about 15% could occur from HEM caused by interactions between a hot Jupiter and a second star in the system). This fraction is notable because a similar number of hot Jupiters orbit their stars on a different plane from the star’s spin axis. Smooth disk migration does not generate the torque required to “misalign” a Jupiter, whereas HEM mechanisms do (in HEM, the Jupiter and an outer companion exchange angular momentum, which generates a lot of torque!). Thus, disk migration and HEM together could explain why some Jupiters are aligned with their star’s spin axis and others are not.