Bald Black Holes Wearing Wigs

Title: No-Hair Theorem for Black Holes in Astrophysical Environments

Authors: Norman Gürlebeck

First Author’s Institution: University of Bremen

Status: Physical Review D, open access

The No-Hair Theorem is a conjecture about the simplicity of black holes. They are called “bald” to reflect the paucity of information necessary to characterise their spacetime – only three parameters at most are needed. The theorem is formulated to describe isolated black holes. A realistic black hole will almost invariably be distorted by its astrophysical environment, e.g. a binary companion, surrounding plasma, accretion disks, or nearby jets. It seems possible that in these cases, the black hole could grow hair and the No-Hair Theorem would break down.

However, this paper shows that the distortions from the surrounding environment do not imply the black hole now has hair. Although our observations of the spacetime an infinite distance from the black hole do change, this is solely due to the external neighbourhood around the black hole, not the distorted black hole itself. In the words of Norman Gürlebeck, the author of this paper:

The No-Hair Theorem remains valid in this more general context: even when engulfed by a complex environment, the black hole resists growing hair.

Bald Black Holes

Isolated black holes are, amazingly, extremely simple. In the words of physicist John Wheeler: “black holes have no hair” (hair being a metaphor here for any messy complicated details). To be precise, black holes have three hairs, meaning that the spacetime surrounding a black hole can be fully characterised by three numbers: mass (M), angular momentum (a) and charge (Q). For a rundown of vocabulary relevant to the No-Hair Theorem, check out this astrobite.

Figure 1: A black hole will be entirely defined by the set of parameters which are its mass, spin and charge respectively. Saying the black hole has “no hair” is a metaphor for this simplicity. Source: http://www.spektrum.de/lexikon/astronomie/keine-haare-theorem/216

Remarkably, this theorem means that physical information that enters a black hole will be lost forever. All memory of the progenitor star will be annihilated and reduced to three little numbers as soon as it collapses into black hole (see Figure 2). Many physicists find this a perplexing and upsetting feature of black holes, as it seems to be in direct contradiction to quantum theory in which information is never truly lost! The conflict between the two theories leads to the black hole information paradox.

Figure 2: The No-Hair Theorem: physical information that enters a black hole is lost forever. No matter what matter contributed to the black hole forming in the first place, and no matter what kind of matter falls into the black hole, the black hole still has no hair! Source: http://gravitation.web.ua.pt/index.php?q=node/362

In fact, three parameters is the most information you will ever need to describe a black hole, according to the No-Hair Theorem. You can get away with even less, depending on what type of black hole you are describing. The Schwarzschild black hole is completely described by only its mass . Only a Kerr-Newman black hole (a rotating,  charged black hole) needs all three parameters to describe it. Astrophysical black hole candidates are likely to be electrically neutral, so the Kerr metric is relevant for realistic black hole spacetimes. See Figure 3 for the requisite parameters corresponding to different types of black holes. This paper proves the result for non-rotating Schwarzschild black holes.

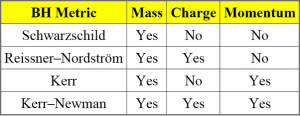
Figure 3: Four different black hole varieties. Source: https://www.quora.com/Are-there-different-kinds-of-black-holes

Black Holes Wearing Wigs

The “No-Hair Theorem” assumes that the black hole is completely isolated from any surrounding astrophysical environment. In this paper, the author has proved the No-Hair Theorem in a more general context: the extended No-Hair Theorem is valid even when the black hole is not isolated, e.g. the black hole could be encircled by a matter disk, see Figure 4.

Figure 3: A black hole surrounded by an astrophysical environment such as a matter disk. This is something like the black hole wearing a “wig”.  Source: http://iopscience.iop.org/journal/0264-9381/page/Focus_issue_on_hairy_black_holes

A static, isolated black hole has a spherically symmetric gravitational field characterised only by its mass . A non-isolated black hole is distorted by surrounding matter; these distortions of the mass distribution are described by a sum of “multipole moments”. In general, a spherical object is described by only the first multipole (i.e. monopole) moment, corresponding to its mass. A distorted object requires higher multipoles to describe it. A black hole surrounded by a disk of matter gains two types of hair: (i) distortions to the geometry outside the black hole and (ii) distortions to the geometry of the black hole horizon – these distortions are called horizon multipoles and correspond to black hole hair. However, just because the black hole has hair on its surface does not mean this hair is visible to an outside observer at infinity!

According to the calculation in this paper, all the higher-order horizon multipoles (except for the mass monopole) that arise from the black hole’s intrinsic hair are extinguished at infinity. For analogy, let us consider for a moment two spatially separated point masses. If the first point mass is isolated, all of its multipole moments (except for the mass monopole) vanish. The second point mass generates a new gravitational field, but the multipole moments of the original point mass are unchanged by the introduction of the second point mass. Now, imagine the first mass is analogous to the black hole and the second mass the external environment. Even if the horizon is distorted by its external environment, the black hole contributes only to the mass monopole moment and not to any of the hair seen by a distant observer – this hair is entirely due to external matter outside the black hole. This is the paper’s extended version of the No-Hair Theorem.

The extended No-Hair Theorem is applicable to more realistic astrophysical scenarios, yielding potential observational implications. For example, some alternative theories of gravity admit black hole solutions with hair, so astrophysical observations combined with the extended theorem could help test and constrain alternatives to general relativity.

• About the Author

About Lisa Drummond

I am an astrophysics PhD student with interests in compact objects and gravitational waves. I studied neutron star interiors for my Masters thesis at the University of Melbourne, Australia and now I am doing my PhD at MIT.