Title: Challenges testing the no-hair theorem with gravitational waves
Authors: Eric Thrane, Paul Lasky, Yuri Levin
First Author’s Institution: Monash University, Australia
Status: arXiv.org, open access
Black holes are believed to be incredibly simple astrophysical objects, described completely by the two parameters mass and spin. This idea is called the “no-hair theorem”; bites discussing this theorem can be found here and here. With the advent of gravitational wave astronomy, we are in a position to thoroughly test the no-hair theorem by probing the gravitational “ringing” of the black hole left after a black hole merger. However, there are some challenges that must be overcome when using gravitational waves to test the no-hair theorem, which the authors of today’s paper investigate.
Coalescence of a Black Hole Binary
When two black holes coalesce, they experience three distinctive phases, yielding the characteristic gravitational waveform – a “chirp” (video link) – depicted in Figure 1. Black hole mergers and their corresponding gravitational wave signals are described in this bite. The key stages are: (1) inspiral (the orbit of the black hole binary gradually shrinks), (2) merger (the two black holes merge) and (3) ringdown (the remnant black hole “rings” by squeezing and stretching).
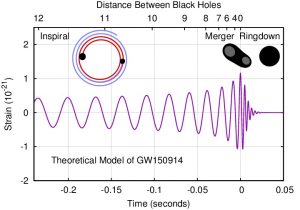
Figure 1: The three phases of a binary black hole coalescence are illustrated (top-view) along the top of the figure and the associated gravitational wave signal as a function of time and distance between black holes is the purple curve. Source: http://ccrg.rit.edu/GW150914
Understanding the gravitational waveform associated with a binary black hole coalescence requires a patchwork of different approaches, seen in Figure 2. The inspiral phase can be described using post-Newtonian techniques, the merger phase with numerical relativity and the ringdown phase using perturbation theory. This paper focuses on the ringdown phase of the black hole coalescence.
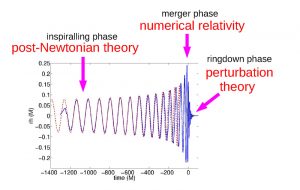
Figure 2: The gravitational wave signal in the three phases of the coalescence of black hole binary. Post-Newtonian methods are valid in the inspiral phase and these calculations are shown by the red dashed line. The blue line shows the numerical relativity calculations in the merger and ringdown stages. Source: http://www.iap.fr/actualites/laune/2016/OndesGr/GravitationalW.html
Ringdown
A black hole is a cosmic bell that will “ring” after colliding with another black hole until it settles down to an equilibrium. Just as the surface of a bell oscillates when struck, the post-merger black hole “rings” by oscillating in shape between a elongated sphere and a flattened sphere. During ringdown, the black hole emits gravitational waves which damp the oscillations and perturbation methods are used to treat this phase. We zoom in on the gravitational waveform produced during the ringdown stage in Figure 3 and observe that the signal takes the form of an exponentially damped sine wave.
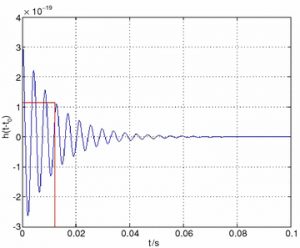
Figure 3: The gravitational wave signal strength as a function of time for the ringdown stage of a black hole binary coalesence event. The signal takes the form of an exponentially damped sine wave. Source: http://authors.library.caltech.edu/5496/1/GOGcqg06.pdf
Results
The frequency and damping time of the ringing black hole are determined entirely by the black hole’s mass and spin. Therefore, it is in principle possible to test the no-hair theorem by checking that a post-merger black hole rings at the correct frequencies and damps at the required rate. In today’s paper, the authors explore how well we can constrain black hole ringdown parameters as the loudness of the ringdown signal increases. The “loudness” of the waveform increases with better sensitivity of the detector and decreases when the event occurs further away.
After the merger, the black hole asymptotically approaches the perturbative state. However, the authors point out that at no point in time is the post-merger waveform precisely described by perturbation theory, because there is always a contribution remaining from the merger phase. They aim to select a time , after which the gravitational waveform is indistinguishable from a damped sine wave (i.e. the remnant black hole has relaxed into its perturbative state). In addition, the ringdown signal becomes weaker as time goes on, because it is exponentially damped.
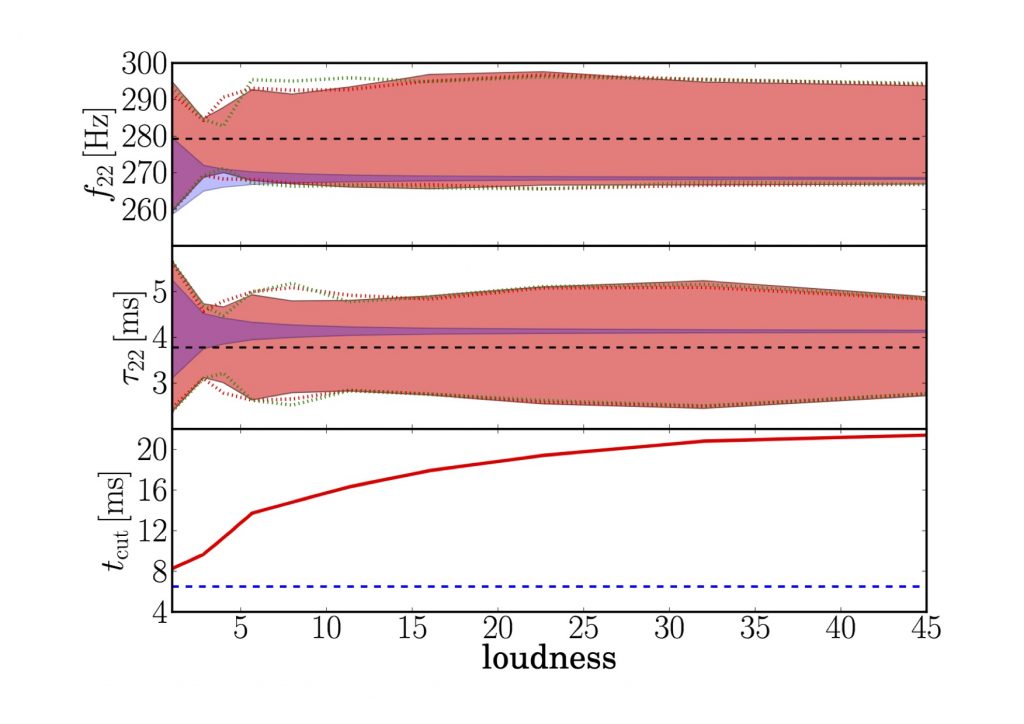
Figure 4: is the ringdown frequency and
is the ringdown damping time. The red shading shows the 95% confidence region. Figure 1 from paper.
Here we have a dilemma. There is a contest between (1) maximising the signal-to-noise ratio by incorporating earlier parts of the signal and (2) waiting for the signal to be well-described by perturbation theory. If we select conservatively, so the signal matches perturbation theory closely, we are discarding louder parts of the signal. Therefore, counter-intuitively, increasing the sensitivity of the detector allows later times to be probed but this does not necessarily yield more precise knowledge of the ringdown frequencies and damping times. Ultimately, this means it may not be possible to test the no-hair theorem with arbitrary precision. Figure 4 shows ringdown frequency
and damping time
as functions of loudness. The red shading shows the 95% confidence region; this region explicitly does not shrink as the loudness of the signal increases, suggesting there is a threshold to the precision of ringdown parameter measurement.
Unfortunately, it is possible that the issue is caused by the lingering non-linearity of the signal from the merger decaying on a similar timescale to the ringdown signal. Alternatively, the authors could be observing an artifact of numerical relativity. In the latter case, it may be possible remedy the scaling behaviour. See the paper for further details about these possibilities.
The authors find that the ringdown frequency and damping time cannot be measured with arbitrary precision, no matter how loud the signal. Consequently, the question of when gravitational wave detectors can unambiguously verify the no-hair theorem is difficult to answer. However, understanding how to deal with the challenges presented in this paper will bring us another step closer!