LISA forewarnings can help LIGO study black holes

Title: Optimizing LIGO with LISA forewarnings to improve black-hole spectroscopy

Authors: Rhondale Tso, Davide Gerosa and Yanbei Chen

First Author’s Institution: California Institute of Technology

Status: Posted on arXiv (open access)

We have now detected several gravitational wave events (including one event with an electromagnetic counterpart, GW170817) since the first was detected on September 14th, 2015. So far, all the signals have been produced by compact binary mergers and observed using the ground-based detector LIGO (Laser Interferometer Gravitational Wave Observatory) and, more recently, VIRGO, another ground-based detector in Europe. In the future, space-based detector LISA (Laser Interferometer Space Antenna) will also detect gravitational waves (see Figure 1), and in particular will be sensitive to the lower-frequency band of the gravitational-wave spectrum.

Today’s paper focuses on how we can exploit LIGO and LISA in conjunction to greatly enhance our understanding of the nature of black holes. LISA will be able to detect the early inspiral stages of the compact binary, thereby giving a “forewarning” of when the signal will be detectable in the LIGO band (the waves become higher frequency later on). With weeks to years of advance warning due to LISA, LIGO can be optimised to make the most of the future detection of the predicted signal.

Figure 1: An artist’s depiction of the LISA detector. Image ource: https://en.wikipedia.org/wiki/File:LISA-waves.jpg

Black hole spectroscopy

In today’s paper, the focus is on how LISA forewarnings can help improve black hole spectroscopy, a technique that measures the frequencies at which black holes “ring.”When you hit a bell or a drum, it vibrates with characteristic frequencies determined by its shape and size. After a while, these frequencies are damped and the ringing stops. Similarly, a black hole will ringdown after being “hit” by another mass (see Figure 1), and the frequencies of the gravitational waves it emits during this period can tell us about the structure of the black hole.

Figure 2: A “ringing” black hole. Image source: http://slideplayer.com/slide/4179737/

If black holes are perfectly described by the Kerr solution, the frequencies they vibrate at will depend on two quantities only: mass and spin. This is a consequence of the “no-hair” theorem for black holes. Measurements of the modes of black hole ringdown can be used to test general relativity and improve our understanding of black holes.

There are different modes of vibration in the ringdown corresponding to the way the black hole changes shape as it is ringing. In this paper, a simple two-mode analysis for the ringdown is used. The dominant ringdown mode is referred to as the “22” mode while the next dominant is usually the “33” mode. If the latter is too weak, it is difficult to perform black hole spectroscopy (this is because black hole spectroscopy involves comparing the two modes). We therefore need to optimise the LIGO detector to improve the detectability of the “33” mode.

Tuning LIGO using LISA forewarnings

Figure 3 (below) demonstrates the main principle behind the paper. First, during the inspiral stage, a gravitational wave is measured by LISA at 0.1 Hz. After 10 years, it becomes visible to LIGO at around 10 Hz (because the frequency of the gravitational wave increases as it emits gravitational radiation and black hole spirals inwards). The orange LIGO detector noise curve has been optimised (through narrowband tuning) to boost the detectability of the weaker “33” mode which occurs at frequency , thereby improving our chances of doing black hole spectroscopy.

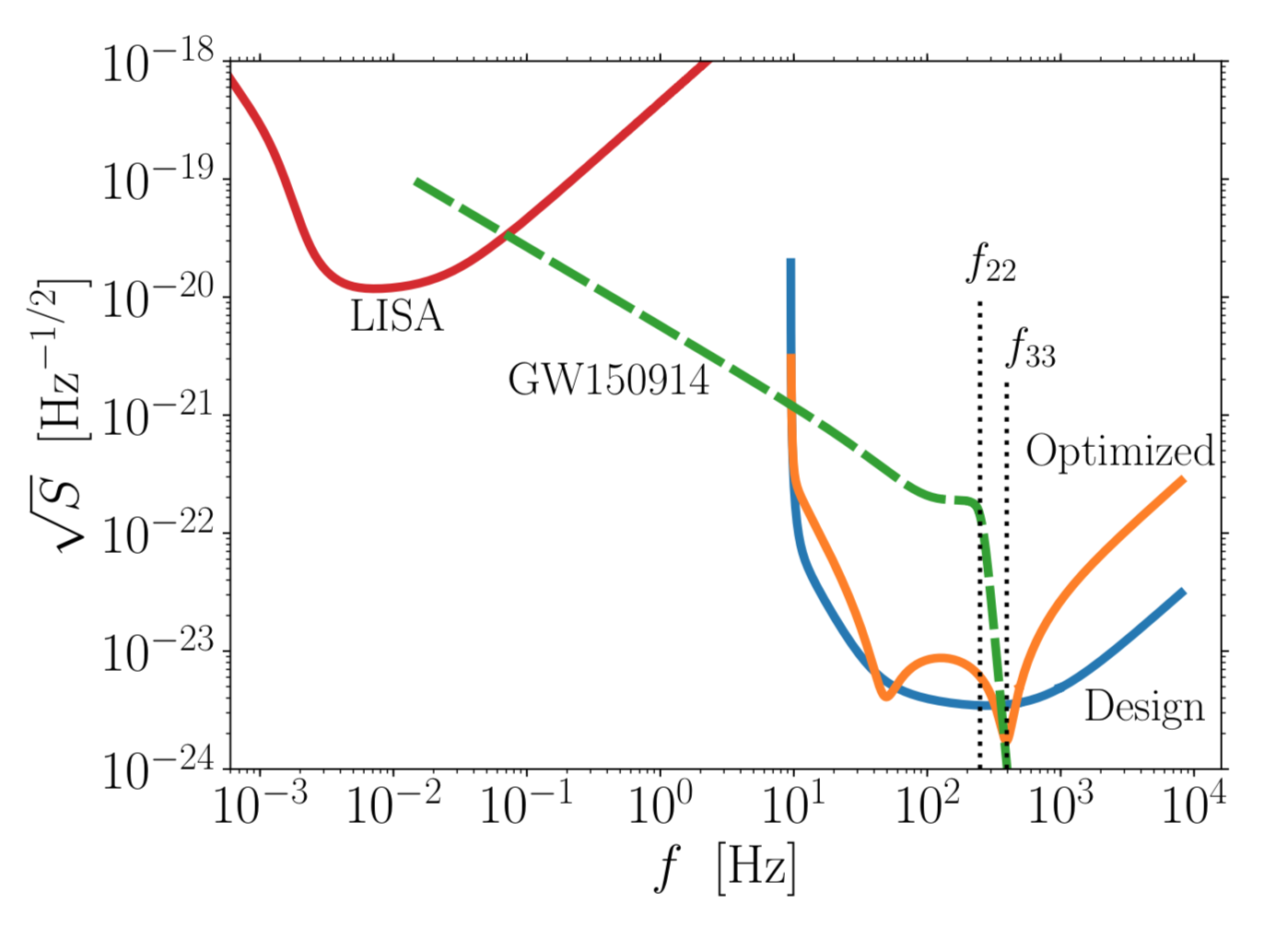
Figure 3: Detection of the same event by LIGO (design and optimised noise curves shown in blue and orange respectively) and LISA (noise curve in red). The green curve shows the gravitational wave frequency and amplitude for a source similar to GW150914. Figure 1 in paper.

How do we actually perform the optimisation of the detector? An obvious optimisation is to simply ensure the detector is operating during that time! Aside from this, detector properties involving the optical set-up (e.g. input optical power, mirror transmissivities, cavity tuning phases) can be adjusted to tune the experiment “on-demand” to the necessary frequency.

To quantify how well LIGO has been optimised to measure the ringdown and minimise noise near the “33” frequency, the following quantity is defined in the paper: , where () means that the optimisation procedure is maximally effective (ineffective).

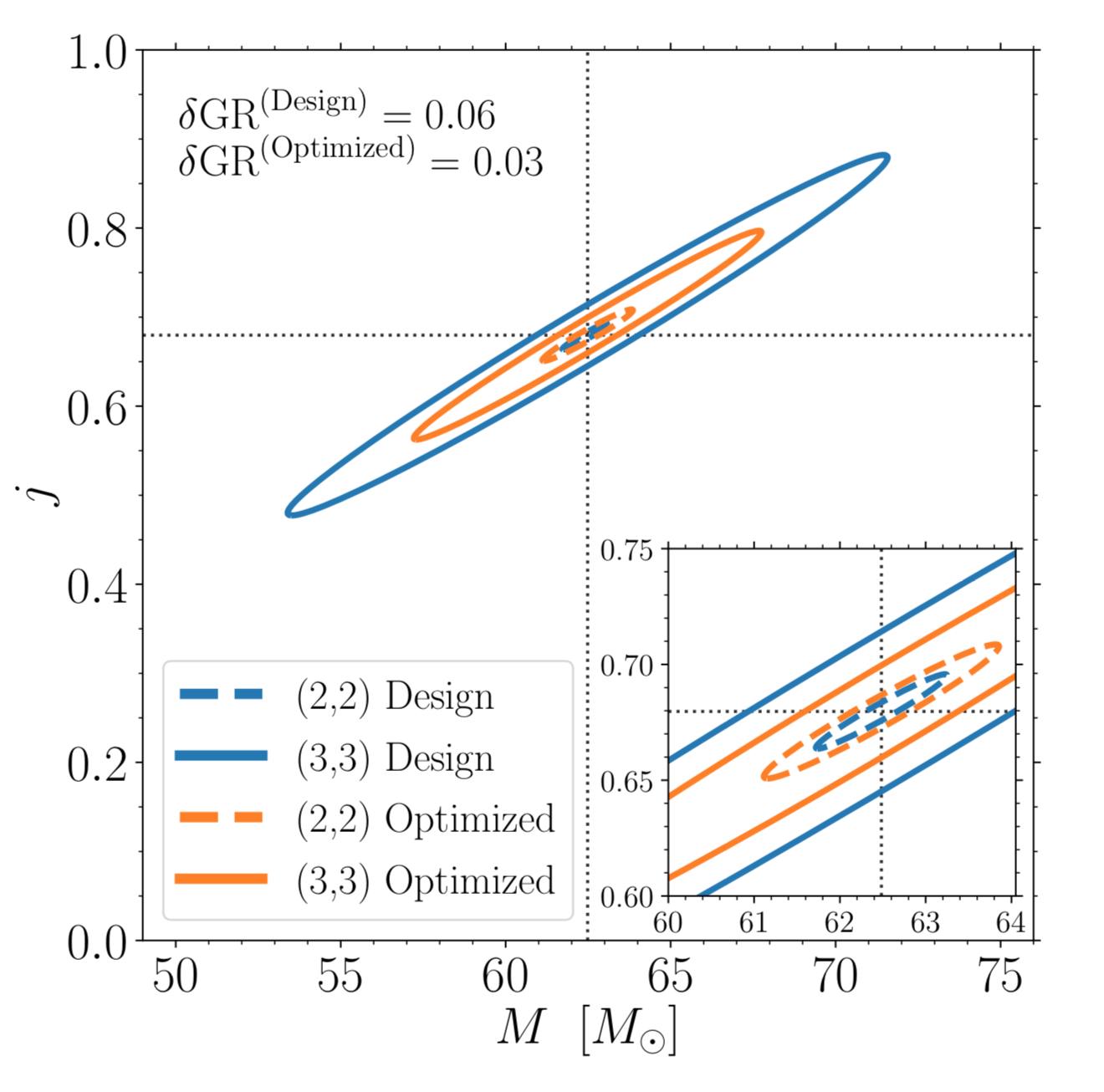
Figure 4: Confidence regions for two parameters for design (blue) and optimised (orange) detector configurations. M and j are the mass and spin respectively. Dotted curves are for the 22 mode and solid curves are for the 33 mode. Figure 2 in paper.

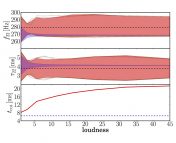
In the standard configuration, the 22 mode is precisely detected (see Figure 4), while when the detector is optimised, the confidence region becomes much larger for 22 but reduces for 33. In the optimised case, the confidence regions are similar in size, due to the boosting of the 33 mode. This leads to a better test of the Kerr metric and improved black hole spectroscopy. For the source depicted in this Figure 4, the optimisation leads to an improvement (defined above) of . With the powers of LISA and LIGO combined, there is a lot of potential to do exciting new science in the future!