Title: Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission
Authors: Antonio Genova, Erwan Mazarico, Sander Goossens, et al.
First Author’s Institution: Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA
Status: Published in Nature, open access
You have probably noticed: when you drop something, it falls. Of the four fundamental forces, gravity is the most present in our daily lives. Ironically, gravity is also the force we understand the least. This is partially because gravity is so weak that it is very difficult to measure. Most of what we have been able to learn about gravity outside of theory has come from either extremely precise laboratory experiments or observations of astrophysical objects that are so large they produce extraordinary gravitational activity not reproducible on Earth. Today’s paper attempts to solidify our understanding of gravity by considering data from a point that experiences some of the strongest gravitational forces in our solar system: Mercury. By analyzing seven years of data from the MESSENGER spacecraft the authors achieve high-precision measurements of some of the most fundamental parameters in the study of gravity.
Methods
The MESSENGER (MErcury Surface, Space ENvironment, GEochemistry, and Ranging) probe was launched on August 3, 2004. After a few flybys of Earth and Venus, it reached Mercury in early 2008. Over the course of seven years it completed three flybys of Mercury before entering orbit in 2011 and finally crashing into the surface on April 30, 2015. As a result of the mission we gained unprecedented insight into the geography, magnetic fields, and atmosphere of Mercury. Most importantly for the purposes of today’s paper, the MESSENGER spacecraft provided precise range measurements which, with analysis of Doppler shifts in radio signals from the spacecraft, tell us exactly where it was. Carefully reconstructing MESSENGER’s ephemeris (its path through space) gives us valuable empirical data. Genova et al. modeled MESSENGER’s orbit while varying several significant gravitational parameters until they could match that data. By simulating the ephemeris with high accuracy they were able to greatly constrain the value of some parameters.
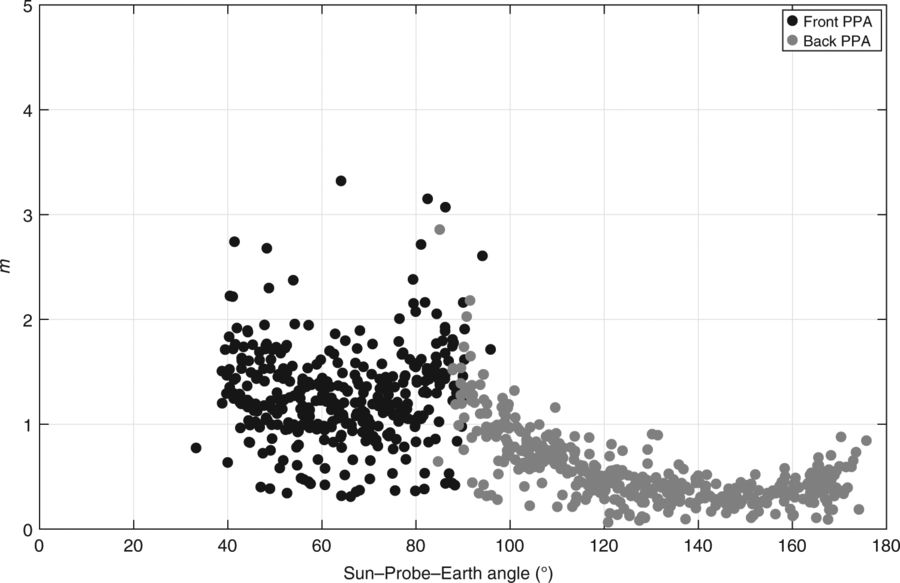
Fig. 1. Range data root mean square (RMS) as a function of Sun-Probe-Earth angle. An angle of 180 degrees would indicate the probe was between Earth and the Sun while an angle of 0 degrees is when the probe is directly behind the Sun. Different colored points correspond to different antennas for reading the data. Fig. 1. in the paper.
A number of complicating factors make this process particularly difficult. The first is that the actual data collection was often quite challenging. As demonstrated in Figure 1, the data became significantly noisier during parts of MESSENGER’s orbit when it is at low Sun-Probe-Earth angle and its signal must pass through large amounts of the solar plasma. Additionally, the curvature of space caused by the Sun’s gravity alters the path of the photons produced by the spacecraft’s radio transmitter and compromises range measurements. Other missions have been able to measure this curvature, but in MESSENGER’s case the effect of curvature is smaller than the effect of the solar plasma so the former is difficult to isolate. In calculating this effect today’s paper had to make assumptions according to Einstein’s theory of general relativity (GR), rather than directly measuring the effect to test the theory. One other complication caused by GR is the Einstein-Lense-Thirring effect which describes the distortion of space-time as something rotates. While the authors would have liked to use this effect to measure the Sun’s angular momentum, it is not independent of other parameters they investigated.
Another significant complication in predicting MESSENGER’s orbit is that the Sun and Mercury are not the only objects in the solar system. The authors needed to consider the gravitational pull of 355 bodies including all 8 planets, the Moon, the Sun, Pluto, and 343 asteroids. It was therefore also necessary to consider the ephemerides of all the other relevant solar system bodies. Furthermore the most significant bodies for MESSENGER, the Sun and Mercury are not point masses. Mercury has a widely varying landscape while the solar interior changes dramatically with time. The work therefore had to account for Mercury’s geography and processes in the Sun.
Results
One of the major goals of today’s paper was to find higher precision values for key gravitational parameters. In particular, the authors paid particular attention to the Nordtvedt parameter, a term that compares various aspects of GR. Proving the Nordtvedt parameter is exactly zero is equivalent to proving the strong equivalence principle of GR which states that it is impossible to distinguish between the force of gravity and the force felt in an accelerating reference frame. Previous experiments using reflective surfaces installed on the moon during the Apollo missions allowed us to constrain the value of the Nordtvedt parameter to (1.0±3.0) x 10-4. Today’s paper constrained it further to (-6.6±7.2) x 10-5.
Another key feature of gravity that we take for granted is that the gravitational constant, G, is in fact constant. The Sun’s mass changes with time via the solar wind and because it is losing mass through fusion to create energy. By measuring how the gravitational strength of the Sun, GM☉ (where M☉ is the mass of the Sun), changed with time and subtracting out the effect of the decreasing solar mass, this paper was able to constrain |Ġ|/G to less than 4.0 x 10-14 per year.
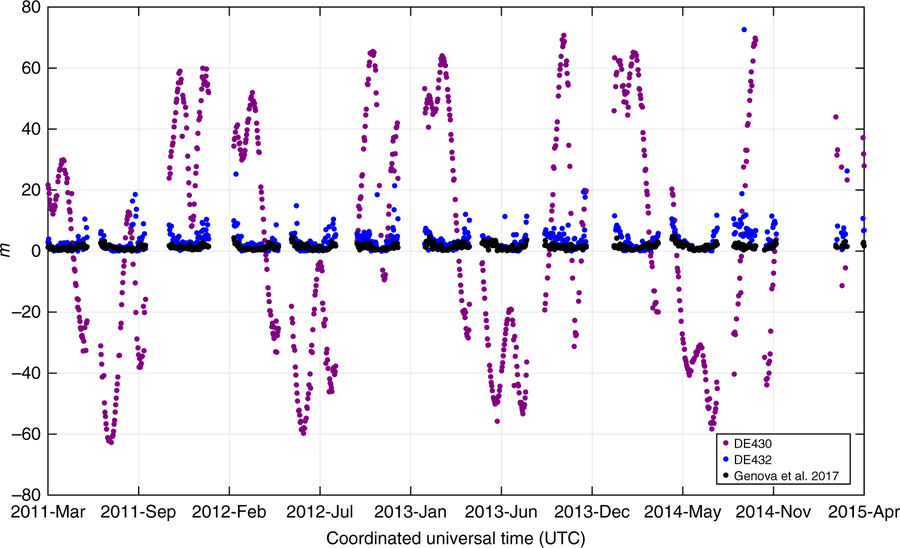
Fig. 2. Errors in various ephemerides calculated for Mercury. The ephemeris created by today’s paper is shown in black. Fig. 3. in the paper.
Since Mercury had the strongest gravitational influence on MESSENGER, it was necessary for the authors to calculate an ephemeris for Mercury with unprecedented accuracy (see Fig. 2). As demonstrated in this work, testing gravity requires increasingly precise calculations. Therefore, in calculating Mercury’s ephemeris the authors have not only brought us closer to an empirically supported theory of gravity but also provided an invaluable resource for future efforts.




Trackbacks/Pingbacks