Authors: Jade Powell
Status: arXiv preprint
On August 17, 2017, the Laser Interferometer Gravitational-Wave Observatory (LIGO) made a historic detection of a gravitational wave signal from a merging neutron star binary. This detection was interesting for many reasons, not least of all because it was the first multi-messenger detection of both gravitational waves and electromagnetic radiation from the same event.
Because gravitational wave detectors are so complicated and sensitive, they are vulnerable to transient, short-duration instrumental or environmental noise, called glitches. An interesting feature of GW170817 was that it occurred during a glitch in one of the detectors (Livingston), causing the automated system to veto the data from that detector and preventing the neutron star merger signal from being distributed immediately. Fortunately, the signal was long and the glitch was short, meaning that the glitch could easily be removed from the data. But we may not be so lucky next time! For example, if the signal itself is not well understood or even completely unknown, we need to know how to deal with detector glitches.
Detector Glitches
Unfortunately for gravitational wave scientists, detector glitches can be difficult to model and can mimic true astrophysical signals – this could make them a big problem for future science runs. The rate of glitches is high: glitches above a signal-to-noise ratio of 6 were observed in 51.5 days of data during the first LIGO science run. When the next LIGO observing run begins, we expect to detect binary mergers even more frequently. This means there is a high probability that future detections will overlap with glitches.
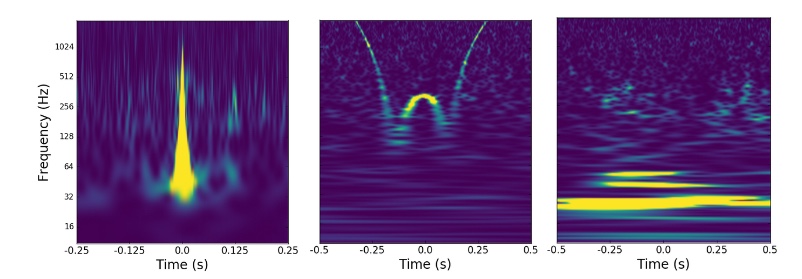
Figure 1. Characteristic examples of the types of transient features that can occur in the LIGO data due to detector glitches. From left to right: a “blip” glitch, a “whistle” glitch and a “scattered light” glitch (which occurs due to scattered laser light in the detector). Figure 1 in paper.
For some glitches, we understand how they are produced and we can observe them in instrumental and environmental monitors of the detectors. However, if a glitch has no known origin and we cannot see it on the monitors – it is hard to determine with certainty whether we are seeing a glitch or a signal. For the neutron star merger, GW170817, the glitch was so much shorter than the signal that it was possible to simply cut out the glitch without losing much information about the signal. However, cutting out a glitch from a shorter length gravitational wave (such as a high mass black hole) may mean removing the entire signal!
Gravitational Wave Signals
So far, we have only detected gravitational wave signals from compact binary systems such as black hole binaries. It is possible that in the future we will detect gravitational waves from supernovae or even completely unknown sources. The focus is on short-duration gravitational waves as these will be the most badly affected by transient detector noise in the form of glitches. For example, a continuous wave from a neutron star would be largely unaffected by a detector glitch, because the glitch could easily be excised from a signal lasting that long.
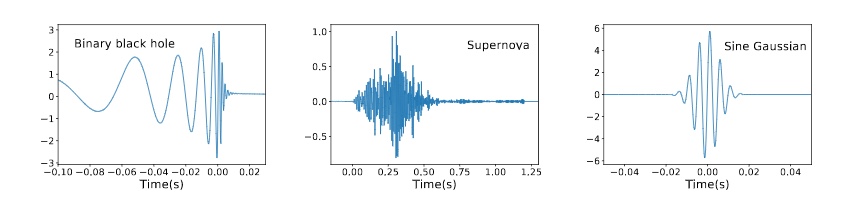
Figure 2: The three types of gravitational waveforms examined in this paper. From left to right: Binary black hole merger, supernova and sine Gaussian. Figure 2 in paper.
To represent a range of possible sources, there are three types of gravitational waveforms examined in today’s paper: short duration black hole binary signals, supernova and sine gaussian (which can be used to model a source when the exact waveform is unknown). These waveforms are shown in Figure 2.
Results
In this paper, Powell selects three characteristic gravitational wave signals (shown in Figure 2) along with the three types of glitches shown in Figure 1. The glitch is then injected on top of the gravitational wave signal. The question this paper investigates is: how hard is it to determine the true values of the astrophysical parameters that produced the signal if there is a glitch in the way? The answer to this question is also affected by the time delay between the signal and the glitch. In general, if there is a large time delay between the glitch and the signal then we will recover a value of the parameter closer to the true value compared to when the glitch occurs at the exact same time as the signal.
For example, in Figure 3 we see the case of a binary black hole signals that was particularly badly affected by a scattered light glitch. In the case, the parameters we are estimating are the chirp mass of the black hole system and the distance of the system from Earth. When the offset is 0.2s, we can see that the true value lies within the grey distribution for both chirp mass and distances (i.e. the true value approximately coincides with the parameter estimate). For time offsets less than 0.2s, the parameter estimates get worse. Because the signal and the glitch are not well-separated in time, it is difficult to distinguish between them, and the glitch contaminates the parameter estimation.
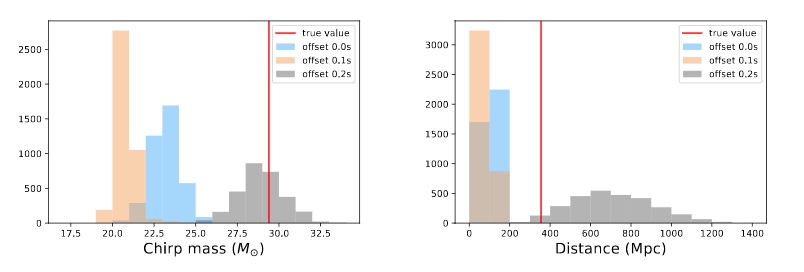
Figure 3. Binary black hole signal that was badly affected by a scattered light glitch. Figure 5 in paper.
Another interesting question probed in this paper is whether having a mismatch between the model waveform and the true gravitational signal detected throws a spanner in the works. If there is a mismatch, glitches can affect the measured astrophysical parameters at a greater time offset, i.e. even when the glitch and the signal are more well-separated in time, the parameter estimates will still be wrong.
This paper convincingly demonstrates that the removal of detector glitches from gravitational wave data is not something we can take for granted – if we are not careful, we can easily predict parameters inaccurately if we don’t account for the presence of a glitch. This is particularly important for signals with unknown waveforms, and will only become more of a problem as detections of gravitational waves become more frequent.




Hey, I know Jade Powell! She works in the same department here at Swinburne. I’ll have to forward her this. 🙂
Why the “offset 0.01s” is the farthest from the true value but not the “offsets 0.0s” in Figure 2?
sorry 0.1s
Hi Fei, good question – I am not really sure. Keep in mind this plot is just an example of a single black hole binary signal to demonstrate the principle. It is better to average out any random effects by looking at many black hole binary signals together. For example, it is possible that the 0.1 s offset can do better at estimating the parameters overall compared to 0.0s but there might be some specific cases where it does worse. Therefore, it might be more informative to look at Figure 4 in the paper which summarises the results for many example black hole binaries.
I think the most important point is that after a certain time offset (0.2s) the effect of the glitch is much less significant.