Title: Transient resonances in the inspirals of point particles into black holes
Authors: Eanna E. Flanagan, Tanja Hinderer
Status: Physical Review Letters, open access
In recent years, we have seen huge breakthroughs in the field of gravitational wave physics. Last year alone, we saw the first multi-messenger detection of a binary neutron star merger and the Nobel Prize in Physics was awarded for the discovery of gravitational waves! So far, gravitational wave discoveries have been made using ground-based observatories LIGO (in the U.S.) and VIRGO (in Europe). In the future, the space-based observatory LISA will be launched. Extreme-mass-ratio inspirals (EMRI) are black hole binaries where one of the black holes is significantly smaller than the other (by at least a factor of 10 000) – these are promising candidates for detection by LISA. If we can detect EMRIs, we will be able to map the spacetime geometry in the neighbourhood of the central (heavier) black hole as well as measure its spin and mass extremely accurately. There is one catch – in order to achieve this, we need very precise theoretical models of these systems. In this paper, the authors draw attention to the presence of transient resonances in extreme-mass-ratio systems: these effects need to be considered when building models for gravitational wave signals from EMRIs.
Orbital Resonances in Astronomy
When talking about resonances, the standard example is a child being pushed on a swing (Figure 1). There are two options: (1) pushing the child in a manner that matches the natural frequency of the swing, so you give the child a boost every time you push and (2) pushing the child at random times (sometimes with the motion of the swing and sometimes against) so that your net contribution averages out to essentially nothing.
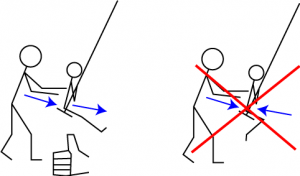
Figure 1: (Left). Pushing the swing to match the existing motion will enhance the effect of the push and lead to resonance. (Right). Otherwise, if the swing is pushed at random times, there won’t be a boost. Image source: https://physics.stackexchange.com/questions/159728/forced-oscillations-resonance
The same thing happens in astronomy in many different systems. As an astronomical object (say, the moon of a planet) orbits another object, there will usually be small perturbations along the path of the orbit. If the period of the object and the perturber are ratios of whole numbers, orbital resonance can occur. Just as in the swing example, the perturber “pushing” the object will have a repeated, periodic contribution to the motion of the object which accumulates over time to amplify the orbit. This often leads to an unstable orbit, but in specific cases the resonance is stable and will self-correct to maintain the resonance. An example of this is the resonance of Jupiter’s moons Ganymede, Europa and Io shown in Figure 2.
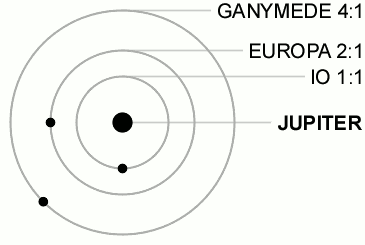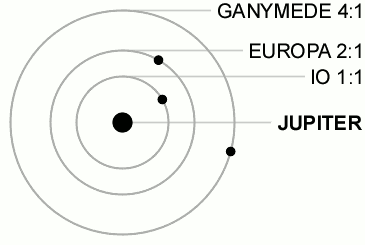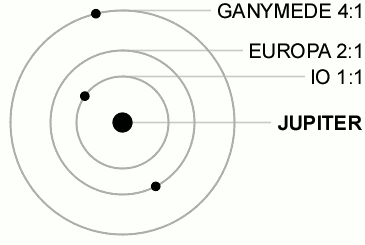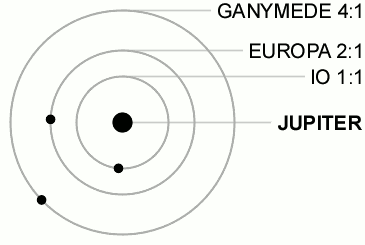
Figure 2: An orbital resonance among Jupiter’s moons. The resonance ratios are the ratio of number of orbits completed in the same time. Image source: https://en.wikipedia.org/wiki/Orbital_resonance
Extreme Mass Ratio Black Hole Binaries
EMRIs occur when a small (stellar mass) compact object, such as a white dwarf, neutron star or black hole, orbits a supermassive black hole (like the one found at the centre of our galaxy) (see Figure 3). The orbit shrinks due to gravitational wave emission until the small object plunges into the central, supermassive black hole. The small black hole takes a very long time to spiral into the supermassive black hole (which could be a million times larger), therefore completing a huge number of orbits before finally plunging in. A large number of orbits means the small black hole will traverse the spacetime in great detail, allowing us to construct a comprehensive picture of the spacetime geometry near a supermassive black hole.
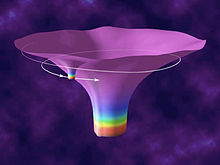
Figure 3: An illustration of the distorted spacetime around an EMRI. The large “dip” is the gravitational potential of the supermassive black hole while the smaller “dip” is that of the stellar mass black hole. Image Source: https://en.wikipedia.org/wiki/Extreme_mass_ratio_inspiral
Black holes exhibit extreme gravitational properties; the theory of General Relativity (GR) is therefore required to study them. There are three different regimes for studying the two-body problem (i.e. two black holes orbiting each other) in GR: (1) the weak-field regime (described by Post-Newtonian Theory) where the black holes are distant from each other, (2) the equal-mass regime, where the black holes are close to each other and of similar mass (described Numerical Relativity) and (3) the extreme mass ratio regime, where one of the black holes is significantly smaller than the other (described by black hole perturbation theory). Note that the large number of inspirals for an EMRI make numerical relativity methods too computationally demanding, but EMRIs naturally lend themselves to perturbation techniques because one of the masses is much smaller than the other – you can treat the spacetime as being perturbed by the small mass. See Figure 4 for a graphical depiction of the different regimes.
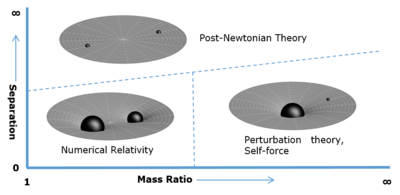
Figure 4: For equal mass black holes, numerical relativity is used. For higher mass ratios, perturbation theory is used. https://en.wikipedia.org/wiki/Extreme_mass_ratio_inspiral
Gravitational waves from EMRIs will be rich with astrophysical information if we can extract it successfully. As mentioned earlier, we can measure the mass, spin and spacetime geometry of the supermassive black hole. If we detect enough of these kinds of events we can also measure the Hubble constant extremely accurately. To do this kind of precision astronomy with EMRIs, it is vital that our theoretical models are accurate enough the match the orbit over all of the cycles – this is a challenging task.
EMRI Orbits and Transient Resonances
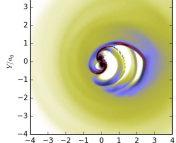
EMRI orbits not only last a long time; they can also be incredibly intricate. (Sidenote: Black hole orbit visualizers can be found here and here if you want to investigate further). The animations below (Figures 5 and 6) illustrate the evolution of an EMRI orbit. These animations were created by Rob Cole and are taken from this article (which contains a more detailed discussion of transient resonances in EMRIs). Figure 5 shows a resonant orbit – note that the orbit traces out a very limited path in the r-cos(theta) plot. Basically, the orbit maintains a constant shape due to the resonance. On the other hand, Figure 6 shows a non-resonant orbit. You can immediately see the difference – the orbit covers the entirety of the r-cos(theta) plot, i.e. the pattern of the orbit is not fixed. Eventually the system is pushed out of the resonant orbit – which is why they are called transient resonances. You can watch an extreme-mass system transitioning in and out of resonances as it evolves in this video by Steve Drasco (a discussion of this video is presented in the previously mentioned article on transient resonances).
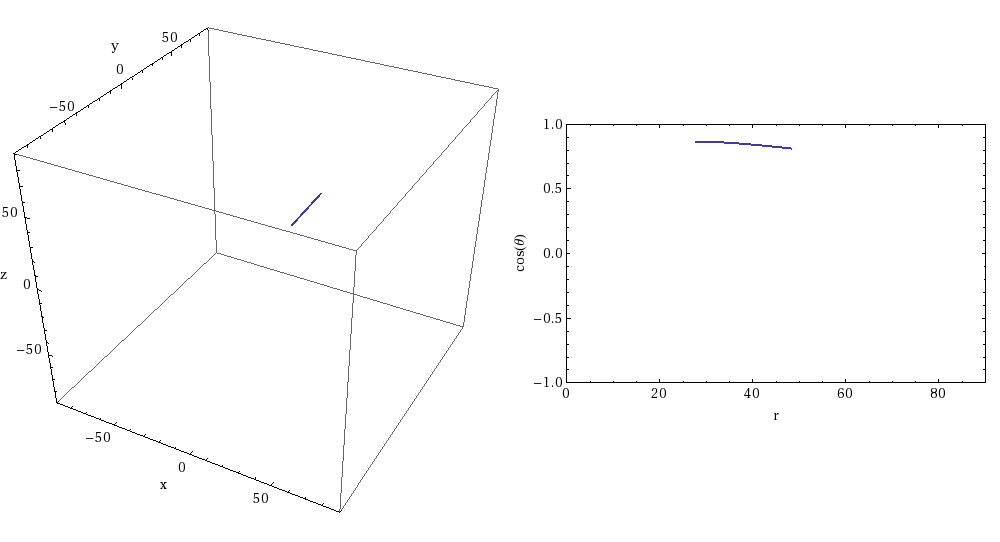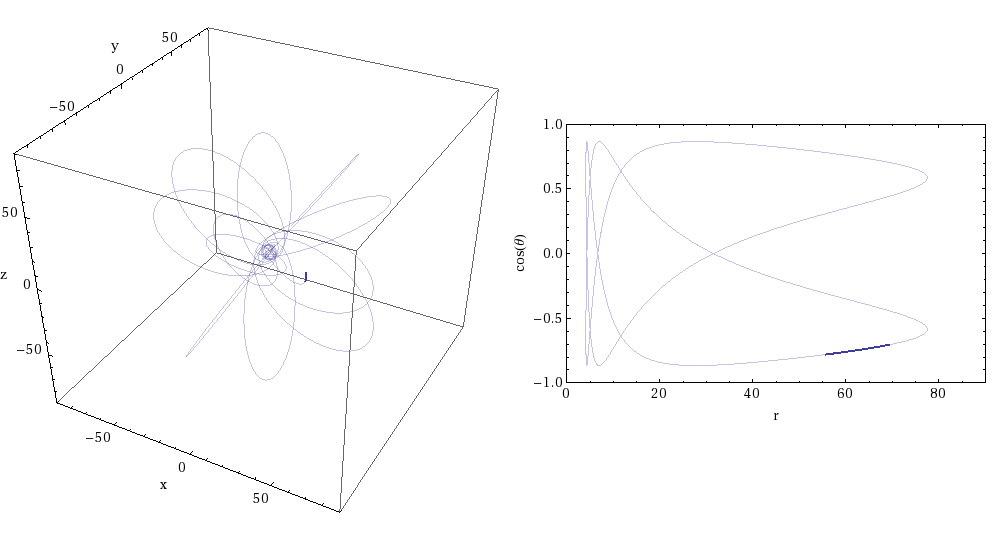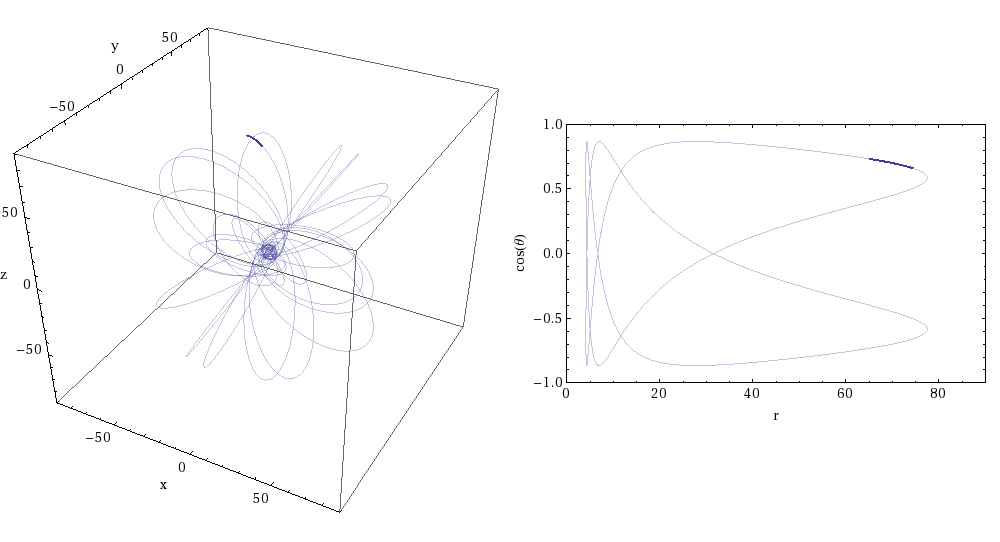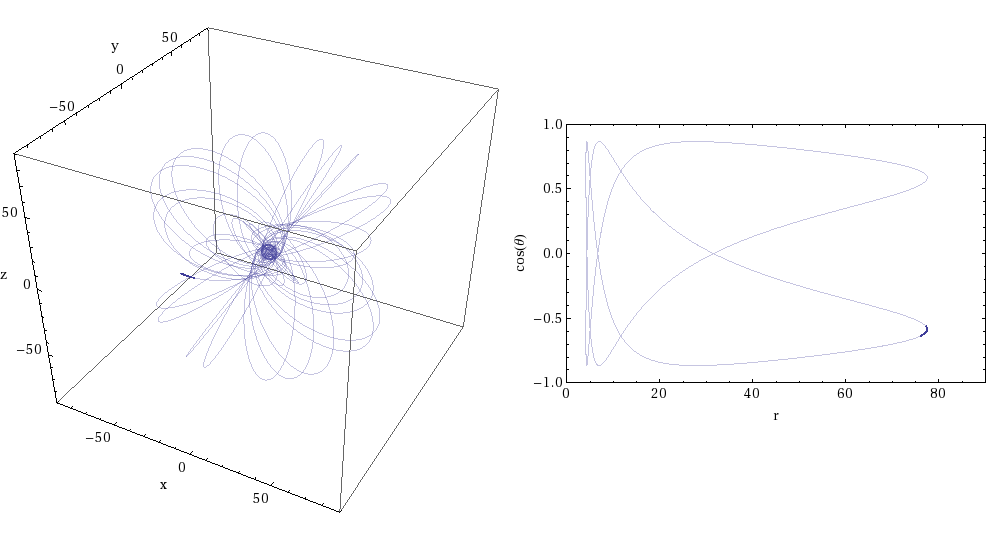
Figure 5: Resonant EMRI orbit. Image credit: Rob Cole; Image Source: https://cplberry.com/2018/03/31/1608-08951/
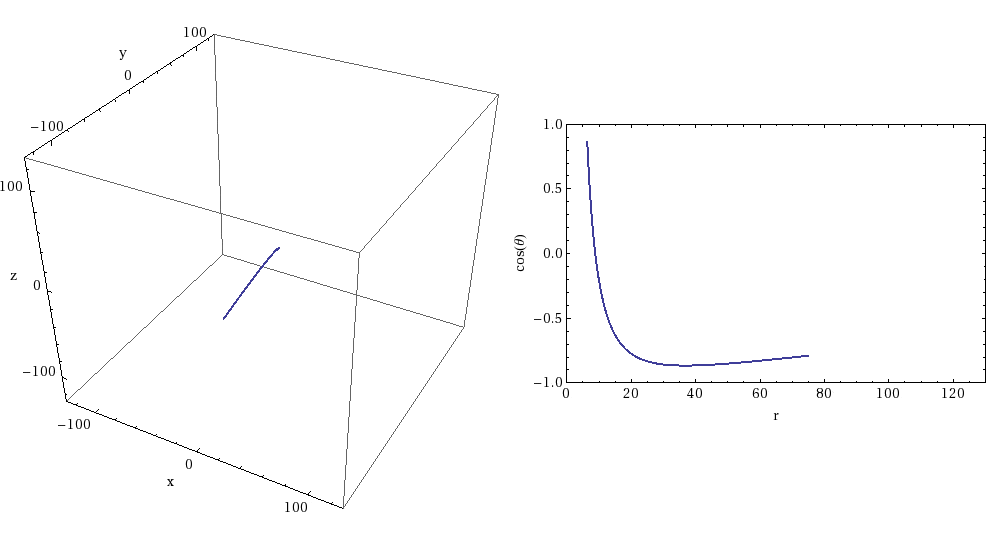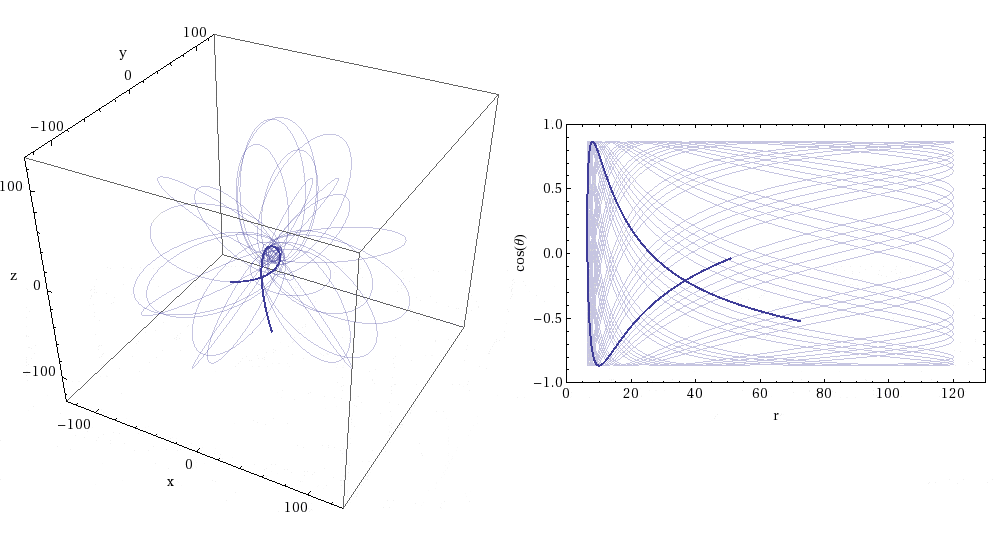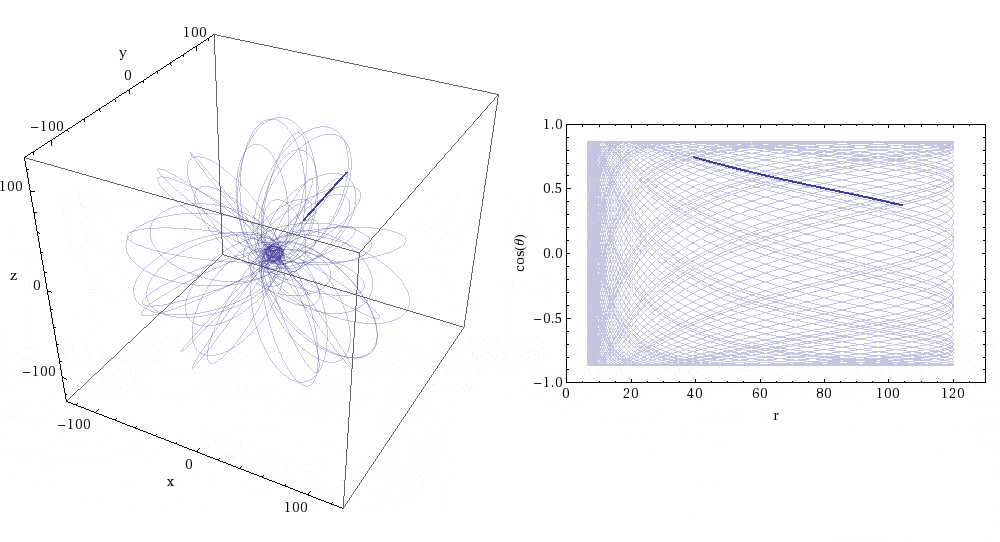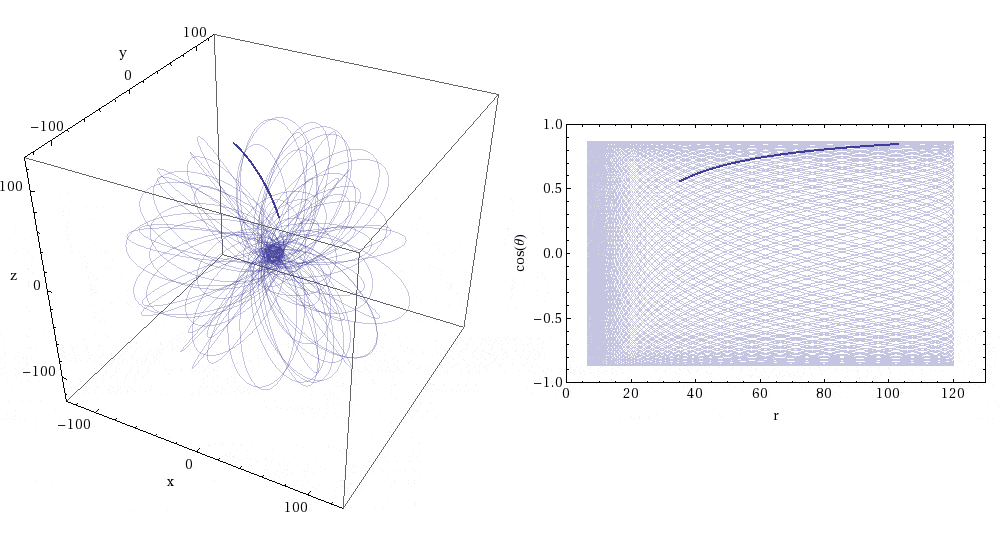
Figure 6: Non-resonant EMRI orbit. Image credit: Rob Cole; Image Source: https://cplberry.com/2018/03/31/1608-08951/
For an EMRI the time taken to complete one orbit is much shorter than the total length of the inspiral. On the long timescales (of the order of time taken to inspiral), an average is taken over many orbits. This approach breaks down when there is a transient resonance because the orbit is tracing the same part of orbital space over and over again (seen in Figure 5).
Key Properties of Transient Resonances in EMRIs
This paper presents three treatments of transient resonances: (1) an order of magnitude calculation, (2) a numerical calculation and (3) a sketch of a formal derivation. These treatments allowed the authors to deduce some key properties of transient resonances in EMRIs which I will summarise below.
- Corrections of the phase of the gravitational wave signal are proportional to the square root of the inverse mass of the small black hole. Therefore, corrections due to resonance effects become large in the extreme mass ratio limit.
- Resonance effects emerge when the ratio of the radial frequency and the polar frequency of the orbit is a rational number.
- Transient resonances about rotating black holes only occur for non-circular, non-equatorial orbits.
The dynamics of EMRIs is very rich and complicated; it is necessary to account for the full details of the orbital motion to build accurate theoretical models. The presence of transient resonances renders certain approximation schemes less accurate. The effect of not accounting for transient resonances when analysing gravitational wave signals was examined in this paper – it was found that neglecting transient resonances leads to a 4% loss of detectable signals.