Authors: K. Kosmo O’Neil, G. D. Martinez, A. Hees, et al.
Status: Submitted to ApJ, 2018 [open access]
Everyone warns you: don’t make assumptions, because when you ASSUME, you look as foolish AS a SUM of Elephant seals, or however it goes.

Figure 1. I’m sorry, they’re just silly-looking animals.
But assumptions are useful, as long as they’re based on facts! On the weekends, for example, I just assume, based on prior experience, that an NYC subway journey will take about twenty minutes longer than it’s supposed to because of crowds and construction. More often than not, I arrive about when I expect based on that assumption.
Of course, if the transit authority magically got its act together, I’d have to update my beliefs—I wouldn’t let an old assumption about slow subways mislead me into showing up awkwardly early for things forever. It would probably only take two or three fast train journeys before I stopped building in that extra 20 minutes. My observations, in other words, would take precedence over my assumptions.
But what if I couldn’t test my assumptions against the real world so effectively? What if I were working from very limited data? In the subway analogy, what if I had moved away from New York years ago, but I were still advising tourists about travel time based on how things used to be? My advice might be better than nothing, but still inadequate or misleading.
Today’s authors investigate: What happens when data are scarce, and you have to let your assumptions guide you? How do you choose your assumptions wisely, so you’re misled as rarely as possible?
Orbits, and the lack thereof
The data these authors investigate isn’t so different from a subway timetable—it’s a list of on-sky coordinates where a celestial body is measured to be, and when. Specifically, they look at the star S0-2, which orbits the black hole at the center of the Milky Way, and the four planets around HR8799, which have been directly imaged (i.e., photographed on the sky, so their positions are known). Figure 2 summarizes what we know about these objects.
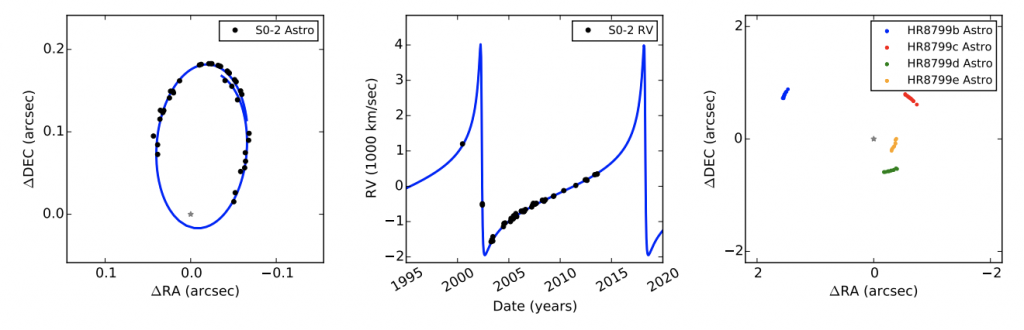
Figure 2. (Left) The on-sky coordinates of star S0-2 (black points) as it traces out its 16-year orbit around the black hole at the center of the Milky Way (gray star), plus the best-fitting orbit (blue line). (Middle) S0-2’s radial velocity at various points in its orbit, plus the best-fitting orbital solution. (Right) The on-sky coordinates of the four planets orbiting HR8799 (gray star). Note that these planets take a long time to orbit their star, so we’ve only witnessed a small fraction of their orbits since the system was first photographed. (Figure 1 in the paper.)
S0-2 has been closely watched for a while—we’ve been able to see it trace out more than a complete orbit around the central black hole. Whatever pre-existing assumptions we might have made about its orbit, they’ve been well and truly tested against the experimental data, and we don’t need to rely on them anymore.
HR8799, though, is a different story. It takes roughly 45 years for the innermost planet (HR8799e, plotted in yellow) to go all the way around, and the planets were only discovered about ten years ago. There’s a surprisingly wide range of possible orbits that fit the limited observations we have so far, and so if we want to decide which possibilities are most likely, we need to rely on our assumptions about how orbits ought to work.
What assumptions are best?
Traditionally, scientists who specialize in orbit-predicting have chosen their assumptions to (they hope) introduce as little bias as possible: to decide, for example, that no value of orbital eccentricity is any more likely than another, a-priori. It’s a fancy way of declaring they’re as agnostic as possible about the best-fitting orbit.
But today’s authors point out that we’re not observing eccentricity, nor any other parameter of the orbit, directly—we’re actually observing on-sky coordinates, as a function of time, and trying to fit for the orbital parameters that match those coordinates best. We should choose our assumptions so that no observation is more likely than any other a-priori. That’s the real way to be as agnostic as we can be.
To test this hypothesis, the authors go on to simulate what happens when you make each of those assumptions and try to fit an orbit with only a few data points. Because the data are simulated, they know the right answer about the orbit, and they can test their results against it. As Figure 3 shows, the “old way” can really bias the results of orbit fitting, and the “new way” performs much better.
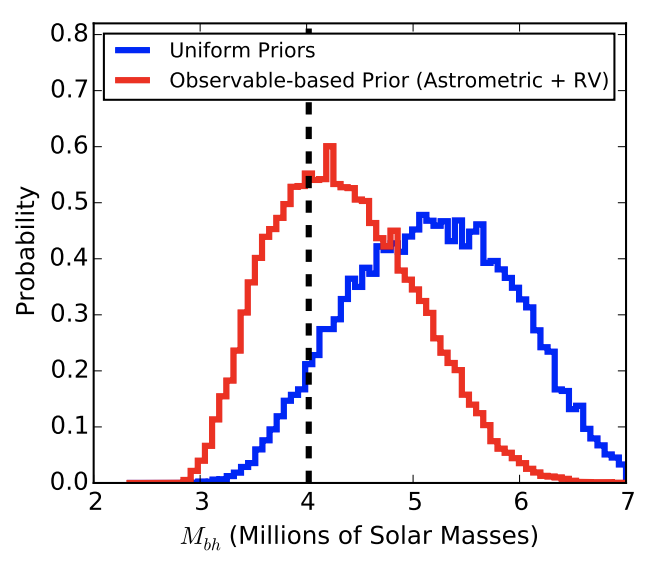
Figure 3. What happens when you try to measure the mass of the Milky Way’s black hole, based on only a few measured coordinates of S0-2? If you adopt the “old” assumptions, you get the blue distribution, which is biased—you’ll conclude that the Milky Way’s black hole is more massive than it really is. If you adopt the “new” assumptions, you’ll get a much more accurate answer. (Adapted from Figure 2 in the paper.)
Unexpectedly, the worse your data is—in other words, the fewer on-sky coordinates you’ve measured, and the more heavily you have to lean on your assumptions—the more likely you are to be biased, if you stick with the old way. It goes to show that we should all re-examine our assumptions every once in a while!
Featured image via.