Title: Observing the influence of growing black holes on the pre-reionization IGM
Authors: Evgenii Vasiliev, Shiv Sethi, & Yuri Shchekinov
First Author’s Institution: Southern Federal University, Rostov, Russia
Status: Submitted to ApJ, open access
Cosmologically important phenomena are typically discussed on the scales of gigaparsecs (Gpc); to give you some idea of the sizes involved, one Gpc could fit approximately 33 thousand Milky Way galaxies end-to-end. That’s a pretty crazy scale and with that in mind today we’ll gain an understanding for how astrophysical events beginning on the order of parsecs can have far-reaching affects cosmologically.
Cosmic Dawn and Reionization
The cosmological period prior to the reionization of the Universe’s hydrogen is typically described as being the cosmic dawn. This stage in the history of the Universe is marked by the formation of the first stars and galaxies. But it doesn’t end there, connecting these large structures throughout the Universe is the Intergalactic Medium (IGM). The IGM during the cosmic dawn consists of mostly neutral hydrogen, and compared to galaxies, is much less dense (10^-27 compared to the density of our Milky Way which is ~10^-19
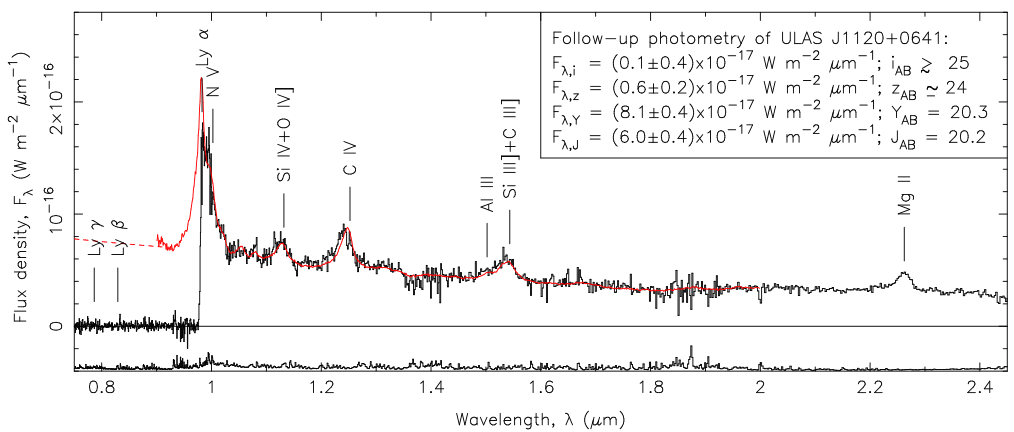
). The UV radiation from these early stars and galaxies are what most astronomers and cosmologists believe led to reionization. Put simply, this ionizing radiation extended symmetrically from these sources and over time these regions of reionized IGM began to overlap leading to complete reionization. While this is our current `best guess’, cosmologists typically wonder: ‘What roles do other structures play during this period?’ One type of galaxy of interest are those containing Active Galactic Nuclei (AGN), which are galaxies with a very dense core with a supermassive black hole (SMBH) at its center that is accreting matter. These AGN are extremely luminous and can produce a lot of X-ray and UV emissions. What we’ll be exploring today is how these SMBH influence the surrounding regions.
Early Black Holes
The very first black holes were most likely few and far between and should have mass ranges several orders of magnitude less than what can be observed today (but in light of new detections we may need to question this). This follows from the fact that for black holes to exist you need some form of already dense matter to collapse under extreme gravitational conditions. These conditions however weren’t as ripe during the cosmic dawn, as matter was just starting to clump together to form behemoth objects such as Population III stars. However the few structures that did begin to form, AGN, or more specifically quasars, were fueled by the type of early SMBHs today’s astrobite investigates.
SMBHs at the center of quasars affect the IGM through reionizing and heating of the gas. This is because as the SMBH accretes local matter hard non-thermal radiation is emitted. So how does the accretion rate of these early black holes influence the surrounding regions? We should expect there to be some relationship between the rate of matter accretion to the distance of influence. Directly following from this, we should also be able to see how observable an object like this might be by using a radio interferometer. Luckily we have the authors from today’s astrobite paper to help answer this for us.
![]()
The authors model the accretion according to the above equation, which relies on the initial black hole mass, , the radiative efficiency
which tells us how easily matter is converted to radiation, and the Eddington time-scale of
(read more here) . This is then related to the resulting ionizing luminosity which they assume to have a power law relationship, and eventually leads us to the ionizing radiation flux.
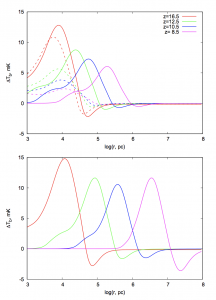
Figure 1: The relationship between brightness temperature and the distance of ‘influence’ of ionizing radiation plotted at several redshifts. The upper plot is for a and the bottom plot for
.
These growing black holes are placed in a host halo of neutral hydrogen where the effects of the ionizing/heating front radius can be related to an observable differential brightness temperature, . The brightness temperature being just the difference between the background Cosmic Microwave Background temperature and the neutral hydrogen 21cm line. Their results for a black hole with an initial mass of 300 solar masses starting at redshift 20 with the radiative efficiencies of
(upper) and
(lower) can be seen in Figure 1. They also compare a non-growing black hole (dashed) as a point of reference.
We can see from Figure 1 that growing black holes should exert the largest influence in terms of distance from the black hole, when compared to non-accreting (dashed). The authors show us that accreting black holes during the early universe can have an influence on the scales of 10 kpc to 1 Mpc. This is of course a very large dynamic range that accreting black holes can influence.
These distances convert to just about the correct angular scales that radio interferometers, such as LOFAR, might be able to probe, which is certainly an exciting prospect. This would be a huge achievement as being able to probe down to the kpc scales and link them to phenomena seen at some of the largest scales could provide us some much needed information on how the earliest black holes formed.



What happens when an object falls into the gravitational field of a black hole towards the event horizon, as seen by an observer far away from the event horizon and stationary with respect to it?
I’ve read that – relative to the observer – the object experiences time dilation because of the tremendous gravitational field near the event horizon, so that light emitting from it becomes redder (longer wavelengths) to the observer. Also, even though the speed of the object as experienced by the object and relative to the event horizon becomes faster, approaching the speed of light, to the observer, because of increasing time dilation, the object’s speed becomes smaller, approaching zero, with light beams emitting from it approaching infinite wavelength. To the observer, the object never passes through the event horizon, but the object itself will not experience time dilation and it will experience its own passage through the event horizon, in its own “comfortable” time.
From all that, I conclude that, to the outside universe (us), matter will take infinite time to get to the event horizon and will therefore never be swallowed by the center of the black hole (where general relativity blows up, the “singularity”). There’s not enough time for that in our universe (well, I shouldn’t really say it that way, but you know what I mean). I think that matter, accumulating just outside the event horizon, will add to the total mass of the black hole, but it will not be concentrated at the center (singularity) of the black hole, and thus any increase of mass of the black hole will be distributed in a region about the event horizon. To me, this is a different animal than say a virgin black hole freshly formed by the collapse of a massive star. Is this all correct? If so, we will observe the black hole growing more massive (accreting matter), but this accreted matter is not at the singularity.
Additionally, going back to the falling object itself, and from the reference of the object itself, doesn’t it experience the event horizon speeding towards itself at an increasing speed that approaches the speed of light? I say that because we are told that light cannot escape the event horizon, and if that’s the case, my conclusion is that the escape velocity from the event horizon must be the speed of light. But it would take infinite energy to accelerate any mass to the speed of light, and a black hole cannot supply infinite energy to the falling object. I thus conclude that the object does experience a passage through the event horizon in a finite time at a speed somewhat less than the speed of light. But I don’t know if my conclusions are valid.
This is all very confusing, to say the least. I appreciate any clarification you can give me.
Regards,
Tom