Title:  (1) The relativistic “looks” of a neutron star, H.P. Nollert, H. Ruder, H. Herold and U. Krauss, in Astronomy and Astrophysics and (2) Light Deflection Near Neutron Stars, U. Krauss, in Relativistic Astrophysics

Status: Open access, see here and here

Today we will look at two papers which attempt to answer the question posed in the title – what does a neutron star look like up-close? In the process, they illustrate (1) a cool feature of relativity which means we can see the far-side of a neutron star from a single vantage point and (2) that this feature is relevant for understanding astrophysical observations.

In the absence of a gravitational field, photon orbits are straightforward – they travel in straight lines! However, in the presence of a strong gravitational field, this is no longer the case. The gravitational forces of a massive body will cause the fabric of space around it to curve. The denser the object, the more spacetime will curve. Photons will follow the contours of space time and therefore travel along curved orbits.

This is true even for stars that are not particularly dense (such as our Sun) – there will still be a small deflection of light that travels past the Sun due to the curvature of spacetime in that region (see Figure 1). This effect was predicted by Einstein and successfully measured in 1919. This was achieved by taking photographs of a region of the sky centered on the Sun during a total solar eclipse (the solar eclipse meant that the positions of stars in that region were visible and not washed out by light from the Sun). Then, another photograph was taken of those same stars when the Sun was far from that patch of the sky. The two photographs where then compared and the conclusion was that light was indeed deflected, confirming the prediction of general relativity.

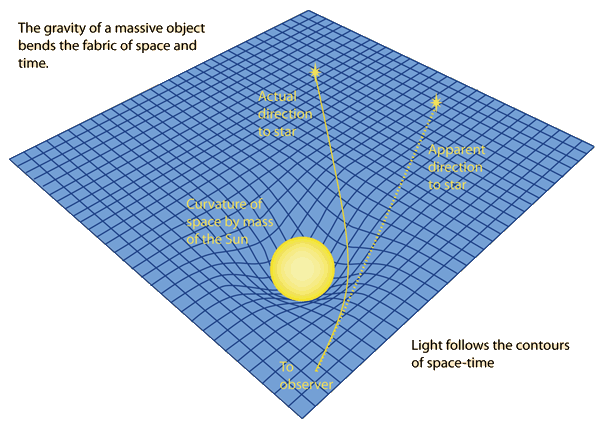
Figure 1: The gravity of the Sun bends the spacetime around it. Light will follow along the curved spacetime fabric. As the light from a background star passes by the Sun, it is deflected, and therefore the apparent position of the star is different to the actual position of the star. Image source: http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/grel.html

Photon orbits around a neutron star

As in the case of the Sun, the gravity around a neutron star causes the spacetime to bend around it. A neutron star contains the mass of the Sun compressed into an object that is the size of a city. Therefore, relativistic effects such as the deflection of light will be even more pronounced near a neutron star compared to the Sun. Understanding the trajectories of photons is crucial for determining what a relativistic object such as a neutron star will look like.

We usually think about space as being three dimensional, i.e. described in terms of three co-ordinates, say . However, in General Relativity, we need four co-ordinates, including time, i.e. . The four co-ordinates are closely interlinked; the value of the fourth co-ordinate (time) has an effect on the other three co-ordinates, hence we need it for a complete description of the geometry of spacetime.

For an object with spherical symmetry (which is very relevant for astrophysics, where gravitating bodies will typically have spherical geometry) the curvature of spacetime will be described by the Schwarzschild metric. This metric tells us how the spacetime will curve near a neutron star and, in particular, how the curvature will change as a function of the mass of the neutron star. To read more about the Schwarzschild metric, you can find some background here and here.

If we consider the equatorial motion of a photon (i.e. we only care about trajectories along a plane through the equator of the star), then the motion of the photon can be described with three co-ordinates, () where and are polar co-ordinates (see Figure 2).

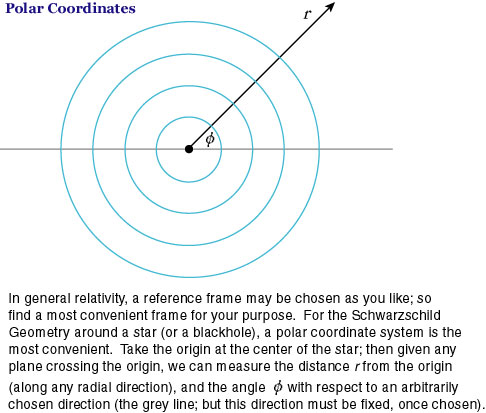
Figure 2: Polar co-ordinates describe the geometry of an equatorial slice through a neutron star. Image source: http://www1.kcn.ne.jp/~h-uchii/schwarzschild.html

The equations of motion can be solved numerically to find the trajectory of a photon (i.e. the angular position of the photon at a particular radius .) We notice that the trajectory is a function of the parameter which is called the impact parameter. The impact parameter is the distance of the photon from a line through the centre of the star (see Figure 3).

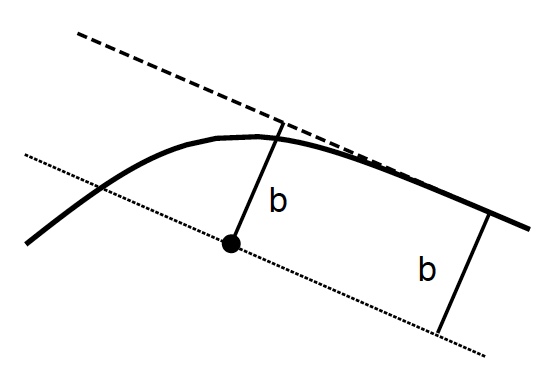
Figure 3. This figure demonstrates the definition of the impact parameter b.The black dot corresponds to the centre of the neutron star.

The value of the impact parameter determines what kind of motion will occur around the neutron star. There are two different regimes: (1) and (2) where is the critical value of the impact parameter. Some examples of the two types of orbits are shown below for the two regimes in Figure 4 and 5 respectively. One thing we notice about the motion of photons in the vicinity of a neutron star is that not only can the photons be deflected as in the case of our Sun, the photons can fall into orbits around the neutron star (see Figure 4).

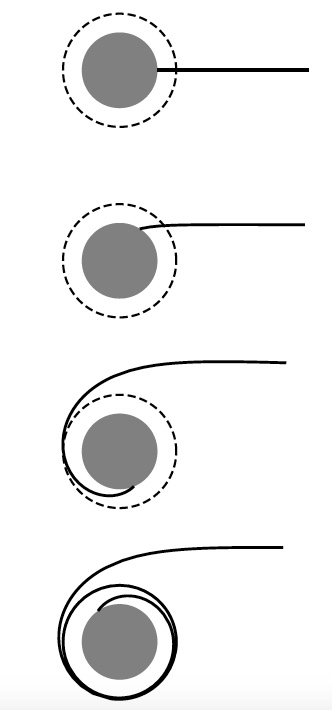
Figure 4: Orbits of a photon around a neutron star in the regime , with increasing from top to bottom. Figure 2 in “Light Deflection Near Neutron Stars”.

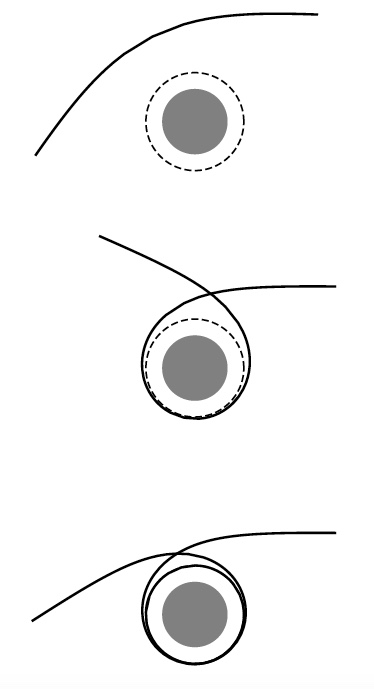
Figure 5: Photon orbits around a neutron star in the regime , with with decreasing from top to bottom. Figure 3 in “Light Deflection Near Neutron Stars”.

Radiation from the neutron star surface

Due to the extreme deflection of photons around a neutron star, what a neutron star looks like is different to the physical reality. Our human minds have adapted to Earth’s gravity and assume that the paths taken by all photons are straight. This is not a valid assumption on the surface of a neutron star, where the gravitational forces are 2×10¹¹ times stronger than on Earth.

The radiation emitted by the neutron star bends in such a way that parts of the rear surface (which would normally be invisible) become visible (see Figure 6).  In fact, it is possible for photons to trapped along an orbit (see Figure 4), therefore causing the entire surface to be visible. The mass of an object determines its Schwarzschild radius . An object with a radius smaller than its Schwarschild radius will be a black hole. Therefore, the closer the the object’s radius is to the Schwarschild radius, the more “black-hole”-like it is, and the more spacetime will curve around it.

Therefore, the quantity that determines the amount of deflection experienced by a photon near a neutron star is the ratio of the Schwarzschild radius to the radius of the neutron star $ latexR/r_s$. As this quantity decreases, more and more of the rear surface of the neutron star is visible, as depicted in Figure 6.

Figure 6: Four images of neutron stars with the same radius but different masses and hence different . The ratio decreases from top to bottom. Figure 6 in “Light Deflection Near Neutron Stars”.

Pulse profiles from neutron stars

Understanding light deflection around neutron stars is important for determining its X-ray pulse profile. This phenomenon is discussed in detail in this astrobite; the authors of today’s bite summarise a simple model which I will discuss briefly here. In an accreting X-ray binary (which is a neutron star in a binary system that accretes from its non-neutron star companion), matter is channeled along the magnetic field lines to the poles, where the kinetic energy is turned into X-ray radiation. We observe regular pulses of this X-ray radiation as the neutron star rotates. Naturally, the radiation emitted close to the poles of the neutron star will be affected by light deflection due to general relativity.

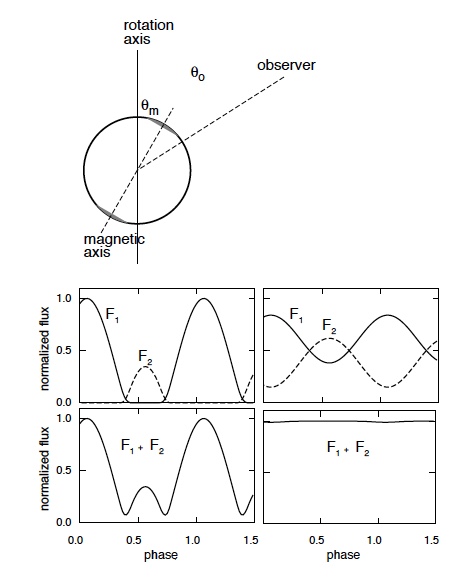
Figure 7: X-ray pulse profiles from an accreting x-ray binary for (right column) and (left column). corresponds to the flux from one of the polar caps and corresponds to the flux from the other polar cap. is the flux from both polar caps combined. Increased photon deflection (i.e. decreasing reduces the modulation in the flux.  Figure 12 in “Light Deflection Near Neutron Stars”.

X-ray emission comes from the poles of the neutron star. Without any light deflection, both poles of the neutron star are only visible during part of the period of the neutron star and vanish at other times, therefore the X-ray flux will modulate over the neutron star’s period. When  is small (the neutron star is very compact), there is substantial light deflection and therefore almost the entire surface of the neutron star is visible all the time. Because both poles are visible all the time, we always see an X-ray flux. This means there will be essentially no flux modulation when is small, as seen in Figure 7.

Relativity is not simply a vital building block of fundamental theoretical physics, it plays a direct role in observational astrophysics. We can use it to understand the radiation we receive from extreme, compact objects such as neutron stars and even learn more about the mysterious content of their interiors – for a more detailed discussion of this topic, check out this astrobite!

• About the Author

About Lisa Drummond

I am an astrophysics PhD student with interests in compact objects and gravitational waves. I studied neutron star interiors for my Masters thesis at the University of Melbourne, Australia and now I am doing my PhD at MIT.

Related posts:

A Pulsar Alone Cloud Watching for General Relativity Observing a Strange Pulsar in X-ray and Radio When is the next glitch on pulsar J0537-6910?