Photons from the “Dark Side” of Neutron Stars Could Help Unravel a Supernuclear Mystery

Title: Pulse profiles of highly compact pulsars in general relativity

Authors: Hajime Sotani & Umpei Miyamoto

First Author’s Institution: Division of Theoretical Astronomy, National Astronomical Observatory of Japan, Tokyo, Japan

Status: Accepted for publication in Physical Review D [open access on arXiv]

Can you see all sides of a sphere simultaneously? While an emphatic “no” is a reasonable answer, you shouldn’t feel quite so confident if the object in question is a compact neutron star. Today’s featured article explores how emission from a very compact pulsar might elucidate the mysterious nature of neutron star interiors. Hang on tight; we’re in for a geometrically challenging ride.

Neutron Star Basics

When a 10-30 solar mass star detonates as a supernova, its core collapses to a density greater than that of an atomic nucleus. The resultant neutron star is often observable as a rotating pulsar if it emits beams of light from its magnetic poles. Though we’ve observed thousands of pulsars since their discovery 50 years ago, very little is known about the equation of state of neutron stars, which describes how matter behaves in their interiors. Illuminating the properties (like mass and radius) of these compact objects will have profound implications for the field of nuclear physics; after all, our inability to study their extreme environments in Earth-based labs means we know very little about the composition and behavior of ultra-dense matter.

While observations of massive pulsars and LIGO’s discovery of a binary neutron star merger have informed and ruled out several theoretical equations of state, Sotani & Miyamoto’s Phys. Rev. D article explores one more potential tool for probing neutron star interiors. A “compactness” parameter can be defined as the ratio of a neutron star’s mass to its radius (M/R). For a typical, less compact neutron star, photons emitted from the back of the star will not be visible to an observer looking at the front side of the star (your intuition was right — you can’t usually see all sides of a sphere at once). However, if a neutron star is very compact (having a high mass and small radius), light emitted on its surface will be gravitationally bent in such a way that an observer could see it from the other side. The authors find that the degree of compactness will significantly affect the pulse profile from a pulsar, meaning that M/R could be measured by analyzing pulsation data. Together with an independent mass or radius measurement (perhaps by the first two methods mentioned in this paragraph), it may be possible to put important constraints on the neutron star equation of state with photons that you didn’t think we could even see.

In the (Highly Geometrical) Weeds

To get a sense of the situation at hand, look at Figure 1. A neutron star’s compactness (M/R) affects the maximum value of the “position angle” ψ, called ψ. As M/R increases, ψ does, too. When that angle becomes bigger than π, we enter the realm where an observer can see a photon emitted from anywhere on the neutron star’s surface.

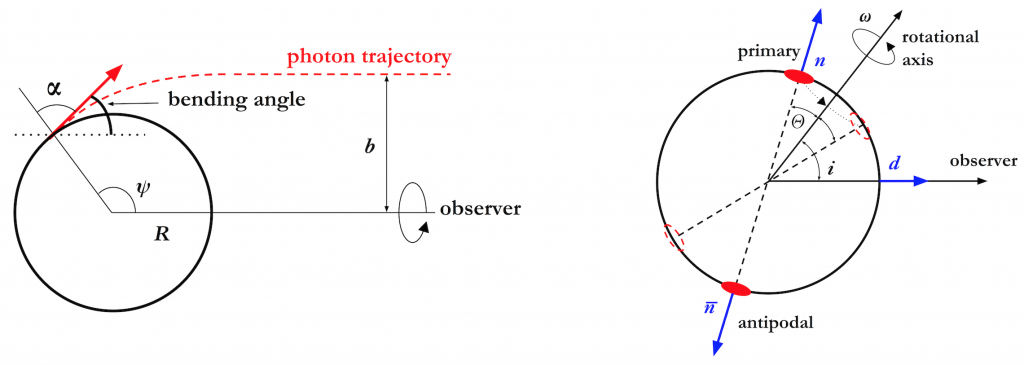
Figure 1: Cartoons of the pulsar’s geometry (not all parameters in the diagram are described in this astrobite). (Left) Ψ denotes the position from which the photon is emitted at angle α. R is the neutron star’s radius. (Right) ω is the pulsar’s rotation (angular velocity). The primary and antipodal (on the opposite side) hotspots are represented by red filled ovals. The vectors n-bar and n point from the neutron star’s center through the hotspots. Angle i is between the pulsar’s axis of rotation and the line of sight to the observer, while Θ is the angle between the rotational axis and n. Closely adapted from Figures 1 and 4 in the paper for clarity.

The authors mainly explore two cases, both of which have ψ  > π. The first is a 2.0-M neutron star with a 10-km radius, and the second has M = 2.21 M and R = 10 km. For a pulsar with two hotspots, one must figure out the total flux by superimposing the flux coming from the primary hotspot (again, see Figure 1) with that which is originating at the opposite, or antipodal hotspot. The primary hotspot’s position as a function of time, ψ(t), is a function of the angle between the rotational axis and the observer (i) and the angle between the primary hotspot vector n and the rotational axis, called Θ.

In Figure 2, the authors show pulse profiles (flux over one rotation of the neutron star) for three distinct cases. The top left and top right panels are for very compact objects, while the bottom panel is for a more typical neutron star with an “invisible” zone on the side facing away from the observer. For the very compact cases, flux is most affected by the primary hotspot’s position relative to the observer for all angular (i, Θ) combinations. For the less compact case, the individual values of i and Θ have a more significant impact on pulse profile. Additionally, it seems that compactness leads to a larger difference between the maximum and minimum observed fluxes for a neutron star. The takeaway is that the pulse profiles for highly compact neutron stars (those without invisible zones) are qualitatively distinct from those belonging to less compact objects, meaning that pulse profile shape may be an effective tool for measuring M/R.

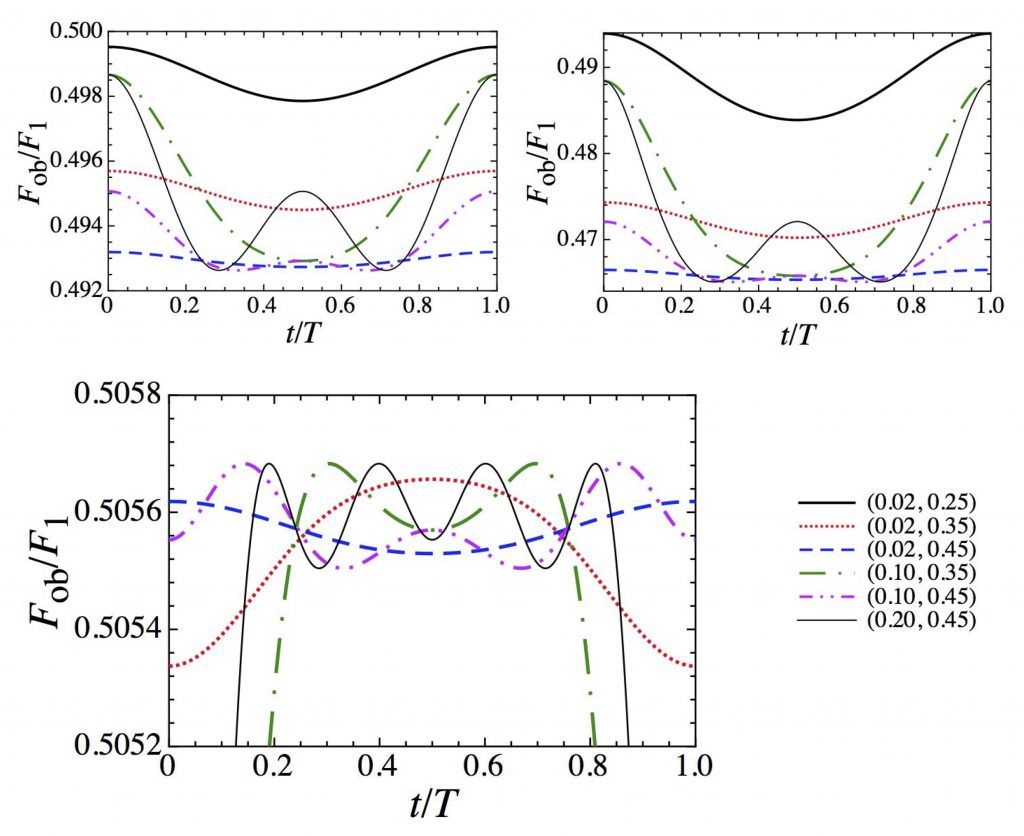
Figure 2: Pulse profiles (flux over one rotation of a compact object) for the cases with M = 2, 2.21, and 1.8 M (top left, top right, bottom). All three have R = 10 km. Observed flux is the superposition of flux from both hotspots. The legend in the bottom right panel applies to all three plots, and shows various (i, Θ) combinations. Selected from Figures 10, 13 and 18 in the paper.

Are “Dark Side” Photons a Novelty, or a Useful Tool?

Because we have discovered 2-M pulsars, and because we know the theoretical upper radius limit for a neutron star is above 13 km, it is completely possible for us to imagine a 2-M, 10.4-km radius neutron star, which is the minimum compactness necessary to see the extreme light-bending effects we have discussed. The authors conclude that, if one can determine the values of i and Θ by other (unspecified) means, it will be possible to measure compactness by examining a compact object’s pulse profile. Such a measurement (M/R) can be combined with other types of observations to determine the individual mass and radius values. While this theoretical method is limited in its complexity (the authors have yet to fully account for rotation, stellar deformation, and other general relativistic effects), it is still an exciting observational prospect. Yet another method for determining the mass and radius of neutron stars is a giant step towards unraveling the neutron star equation of state.

• About the Author

About Thankful Cromartie

I am a graduate student at the University of Virginia and completed my B.S. in Physics at UNC-Chapel Hill. As a member of the NANOGrav collaboration, my research focuses on millisecond pulsars and how we can use them as precise tools for detecting nanohertz-frequency gravitational waves. Additionally, I use the world's largest radio telescopes to search for new millisecond pulsars. Outside of research, I enjoy video games, exploring the mountains, traveling to music festivals, and yoga.

Related posts:

Tiny Stars in a Tiny Orbit: A New Ultracompact Binary Timing is Everything: A Pulsar in Orbit Why Are Pulsar Planets Rare? The Mysterious Pulsars That Switch On and Off