- Title: A Millisecond Pulsar in a Stellar Triple System
- Authors: S. M. Ransom, I. H. Stairs, A. M. Archibald, et al.
- First Author’s Institution: National Radio Astronomy Observatory, Charlottesville, Virginia, USA
- Paper Status: Published online by Nature
One of nature’s best clocks is a millisecond pulsar. These exotic stellar corpses are neutron stars: incredibly dense, rotating hundreds of times per second, and emitting powerful jets or beams of light. This creates a “pulsing” effect, much like a lighthouse. Single pulsars are such precise timepieces that the first one discovered was a serious contender for signs of alien life. Now we know that pulsars are exhausted stellar cores—all that remains at the end of a massive star’s life. But what happens when a lone interstellar beacon has a dance partner?
This paper by Ransom et al. reports the first pulsar in a triple system, called PSR J0337+1715*. This isn’t just a pulsar and one other star orbiting one another, but a complex interaction of three bodies: the pulsar, and two white dwarf companions.
Watch a short, silent animation of the system here!
Hey, Your Clock is Broken
They say a broken clock is right twice a day. Not so for millisecond pulsars! The arrival time of each pulse can be measured extremely precisely with radio telescopes, and any delays can be used to create a physical model of the pulsar and its gravitationally interacting dance partner(s). In the top two panels of the figure below, a delay in pulse arrival time is plotted verses time. If the pulsar was a truly perfect clock, and not moving at all relative to us, we would see a flat line. Instead, oscillations with different frequencies appear as telltale signatures of orbital motion. The pulses’ measured times of arrival are actually a combination of two effects: light travel time due to the pulsar’s orbital motion, and the Einstein delay, due to a combination of special and general relativity.
One of the white dwarf companions orbits the pulsar with a 1.6-day period, and its effects appear in panel (a) below. The other white dwarf orbits much farther out with a 327-day period, visible in the zoomed-out panel (b) below. This arrangement, with two bodies zooming around each other and a third more leisurely companion farther out, is called a hierarchical triple system.
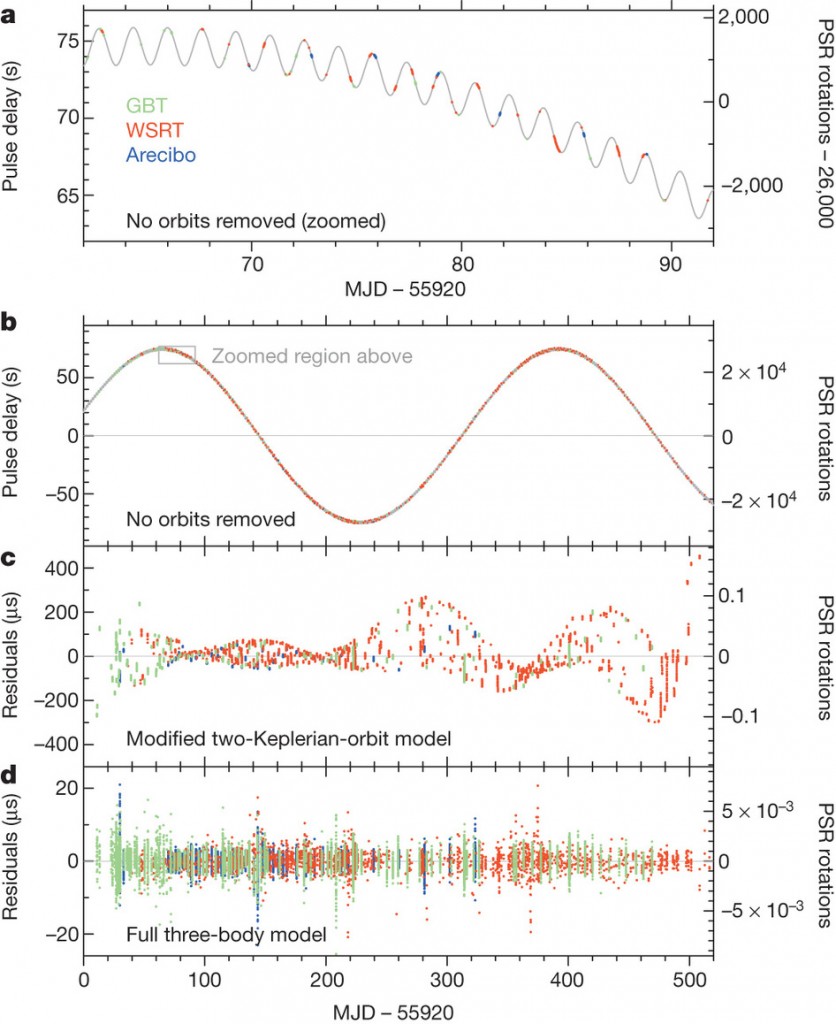
Pulse arrival times from a steadily ticking pulsar show telltale signs of orbiting companions. Panels (a) and (b): oscillating signals from each of two white dwarf companion stars. Panel (c): a simple model assuming both white dwarf companions obey Keplerian motion doesn’t fit the data well. Panel (d): a model that allows all three bodies to gravitationally interact does a much better job.
To model the orbits of the two white dwarfs around the pulsar, the authors try using Kepler’s Third Law. However, three-body systems do not have a tidy analytic solution. This is demonstrated in panel (c) above—a pair of Keplerian orbits fails to accurately model the delayed pulse arrivals. The residual plot shows a pattern, which is a red flag indicating the model does not fit the data. To arrive at a better solution, they use a Markov chain Monte Carlo three-body timing solution to fit a suite of 14 parameters and minimize the residuals. This result is much better, and nails down physical properties for all three members of the system. The resulting pattern-free residuals are shown in panel (d) above.
A Pulsar’s Life
Today in the PSR J0337+1715 system, we see a 1.4 solar-mass neutron star (the pulsar), a 0.2 solar-mass white dwarf (close companion), and a 0.4 solar-mass white dwarf (distant companion). But all of these objects are stellar corpses—they’re what remains after a star has exhausted its hydrogen fuel and blown off its outer layers. The authors outline a possible story for how this triple system came to be:
Once upon a time, at least three stars were born in a multiple system. The most massive star evolved fastest, went supernova, and became a neutron star. Two companions survived the explosion. After a billion years or so, the outermost companion became a red giant, and dumped mass onto the inner binary until it became a white dwarf. After another billion years, the closer companion followed suit and transferred enough mass to the neutron star to “spin it up.” Over time, the orbits tugged on each other and became gradually more circular and closer to sharing the same plane, until they became the system we see today.
Putting Gravity to the Test
An exciting application for this system is a test of one piece of Einstein’s theory of general relativity, called the strong equivalence principle. This says that the orbital motions of bodies with strong self-gravity (such as a neutron star pulsar) are the same as those with weak self-gravity (such as a relatively low-mass and less dense white dwarf). While general relativity has been confirmed by every experiment we’ve tried so far, it cannot explain the workings of the Universe on very small scales, so it is important to continue testing the theory’s predictions using nature’s most extreme laboratories.
*Astronomers think up the most creative names. Also, if you were watching closely, you may recall a brief mention of this discovery at the recent AAS meeting.




